当前位置:首页 > 中学教育 > 初中教育 > 吉林省白城市通榆县2022年九年级第六次模拟考试数学试题
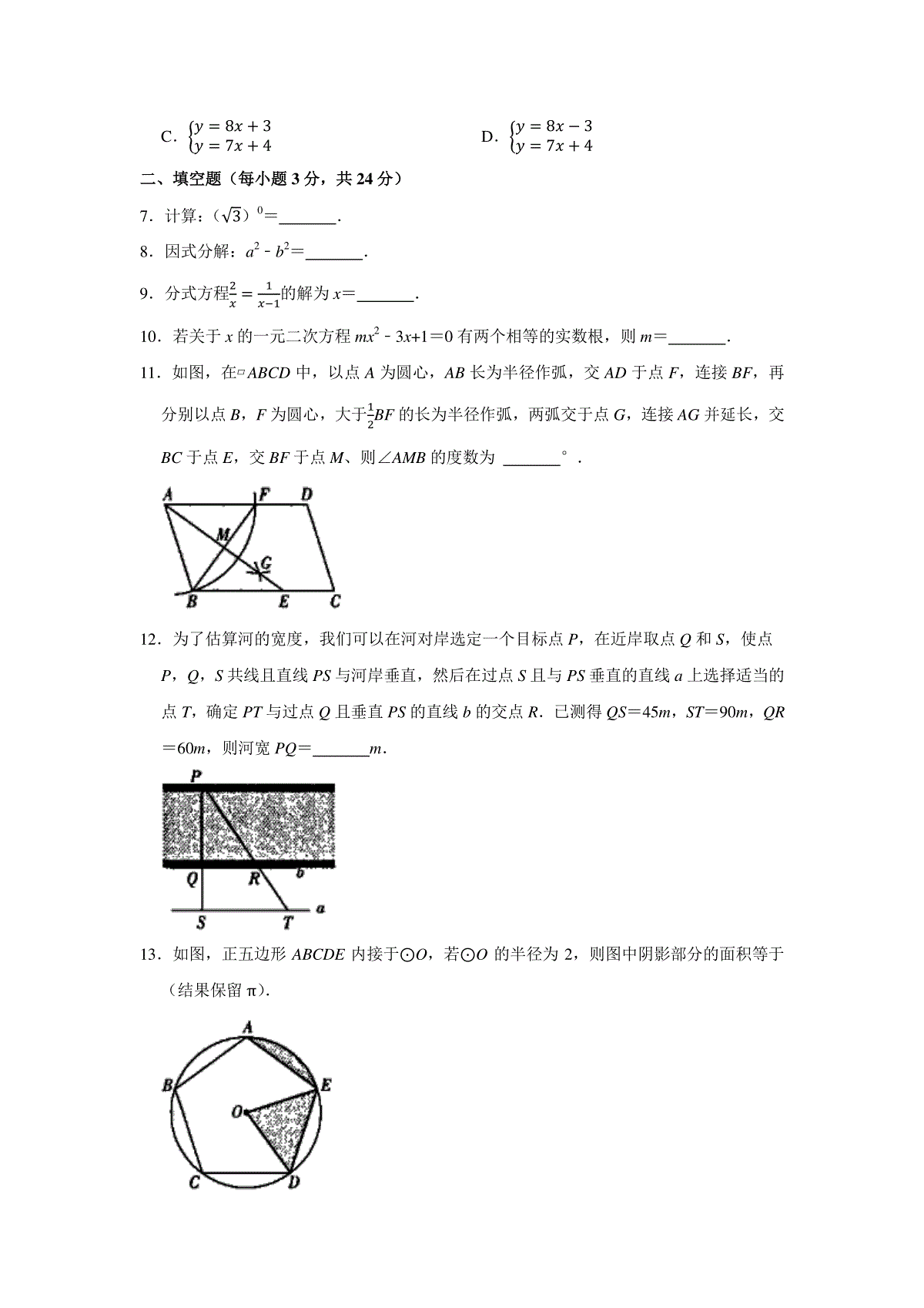
学科网(北京)股份有限公司吉林省白城市通榆县2022年九年级第六次模拟考试数学试题一、单项选择题(每小题2分,共12分)1.实数a在数轴上对应点的位置如图所示,则a的值为()A.1B.0C.﹣1D.﹣22.2022年北京冬奥会共有91个国家参加,运动员共有2880人.数据2880用科学记数法可表示为()A.2.88×104B.28.8×103C.2.88×103D.0.288×1043.不等式2x<x﹣2的解集是()A.x>﹣1B.x>﹣2C.x<﹣1D.x<﹣24.如图,一个几何体由5个大小相同,棱长为1的小正方体搭成,下列说法中正确的是()A.左视图的面积为4B.主视图的面积为4C.俯视图的面积为3D.三种视图的面积都是45.如图,四边形ABCD是圆的内接四边形,∠BAD=108°,E是BC延长线上一点,若CF平分∠DCE,则∠DCF的大小是()A.58°B.56°C.54°D.52°6.《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?“译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱,问人数、物价各多少?”若设人数为x人,物价为y钱,可列方程组为()A.{𝑦=8𝑥+3𝑦=7𝑥−4B.{𝑦=8𝑥−3𝑦=7𝑥−4学科网(北京)股份有限公司C.{𝑦=8𝑥+3𝑦=7𝑥+4D.{𝑦=8𝑥−3𝑦=7𝑥+4二、填空题(每小题3分,共24分)7.计算:(√3)0=.8.因式分解:a2﹣b2=.9.分式方程2𝑥=1𝑥−1的解为x=.10.若关于x的一元二次方程mx2﹣3x+1=0有两个相等的实数根,则m=.11.如图,在▱ABCD中,以点A为圆心,AB长为半径作弧,交AD于点F,连接BF,再分别以点B,F为圆心,大于12BF的长为半径作弧,两弧交于点G,连接AG并延长,交BC于点E,交BF于点M、则∠AMB的度数为°.12.为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S共线且直线PS与河岸垂直,然后在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.已测得QS=45m,ST=90m,QR=60m,则河宽PQ=m.13.如图,正五边形ABCDE内接于⊙O,若⊙O的半径为2,则图中阴影部分的面积等于(结果保留π).学科网(北京)股份有限公司14.如图,在四边形ABCD中,∠ABC=90°,AB=4,BC=3,CD=2.E为AD的中点,连接BE,则BE的最大值为.三、解答题(每小题5分,共20分)15.先化简,再求值:(a+1)2﹣a(a﹣1),其中a=13.16.某商场举办抽奖活动,规则如下:在不透明的袋子中装有1个黑球和2个白球,这些球除颜色外无其他差别,顾客每次摸出1个球,若摸到黑球,则获得1份奖品;若摸到白球,则没有奖品.(1)若小明从袋子中随机摸出1个球,则小明获得奖品的概率为.(2)若小明有两次摸球的机会(摸出后放回),用画树状图或列表的方法,求小明获得2份奖品的概率.17.某校三年共购买计算机140台,去年购买的数量是前年的2倍,今年购买的数量又是去年的2倍.求前年这个学校购买了多少台计算机.18.如图,▱ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.求证:△ABE≌△CDF.四、解答题(每小题7分,共28分)19.如图是4×3的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,△ABC的顶点均在格点上,请用无刻度的直尺按要求作图.(1)在图中,分别取AB,BC的中点D,E,并连接DE.(2)在图中,作△BDE的高线BH.(3)△ABC的边AC上的高线的长度为.学科网(北京)股份有限公司20.由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习的方式:A.网上自测,B.网上阅卷,C.网上答疑,D.网上讨论.为了解学生对这四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查的学生从这四种学习方式中选择自己最喜欢的一种.根据调查结果绘制成如下两幅不完整的统计图;根据统计图提供的信息,解答下列问题.(1)本次共调查了名学生.(2)在扇形统计图中,p的值是,D对应的扇形圆心角的度数是°.(3)请补全条形统计图.(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生的人数.21.如图,▱ABCD中,顶点A的坐标是(0,1),AD∥x轴,一次函数y=x﹣1与反比例函数y=𝑘𝑥的图象都经过B,D两点.(1)求k的值.(2)求▱ABCD的面积.学科网(北京)股份有限公司22.如图,建筑物的高CD为10m.在其楼顶C处测得旗杆底部B的俯角α为45°,旗杆顶部A的仰角β为20°.求旗杆AB的高度.(结果精确到0.1m,参考数据:sin20°=0.34,cos20°=0.94,tan20°=0.36)五、解答题(每小题8分,共16分)23.在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”“猫”距起点的距离y(m)与时间x(min)之间的关系如图所示.(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是m/min.(2)求直线AB的函数解析式.(3)求“猫”从起点出发到返回至起点所用的时间.24.如图,在△ABC中,点P是AB的垂直平分线l上的一点,点D是AB与直线l的交点,PA=PC,AB﹣8,PD=1.学科网(北京)股份有限公司【猜想】如图①,当点C在直线l的左侧,∠APC=90°时,∠B=°,点C到直线l的距离为.【探究】如图②,当点C在直线l的右侧,∠APC=90°时,求BC的长.【拓展】当点C不在直线l上,且△ABC为等腰三角形时,直接写出BC的长.六、解答题(每小题10分。共20分)25.如图,在矩形ABCD中,AB=5cm,BC=3cm.动点P,Q分别从点A,B出发,同时以1cm/s的速度沿折线ADC和BAD分别向终点C,D运动.设运动时间为x(s)(x>0),直线PQ,BQ,PC,BC所围成的图形的面积为y(cm2).(1)当点P与点D重合时,AQ的长为cm.(2)求y关于x的函数解析式,并写出自变量x的取值范围.(3)当△PBQ为直角三角形时,直接写出x的值.26.在平面直角坐标系中,函数y={𝑥2−2𝑥+𝑚(𝑥≥1)12𝑥2+𝑥−𝑚(𝑥<1)(m为常数)的图象记为G.(1)若点(2,1)在图象G上,求m的值.(2)若点(m,﹣1)在图象G上,m的值为.(3)若点P(﹣1,m),点Q(2,m),连接PQ.①当图象G与线段PQ只有两个交点时,求m的取值范围.②将线段PQ绕点P逆时针旋转90°,得到线段PM,并连接QM,当△PQM与图象G有且只有两个交点时,直接写出m的取值范围.学科网(北京)股份有限公司

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 4页
4页
 2页
2页
 3页
3页
 4页
4页
 9页
9页
 8页
8页
 2页
2页
 9页
9页
 8页
8页
 9页
9页
本文标题:吉林省白城市通榆县2022年九年级第六次模拟考试数学试题
链接地址:https://www.777doc.com/doc-12514111 .html