材料力学考研真题十一套

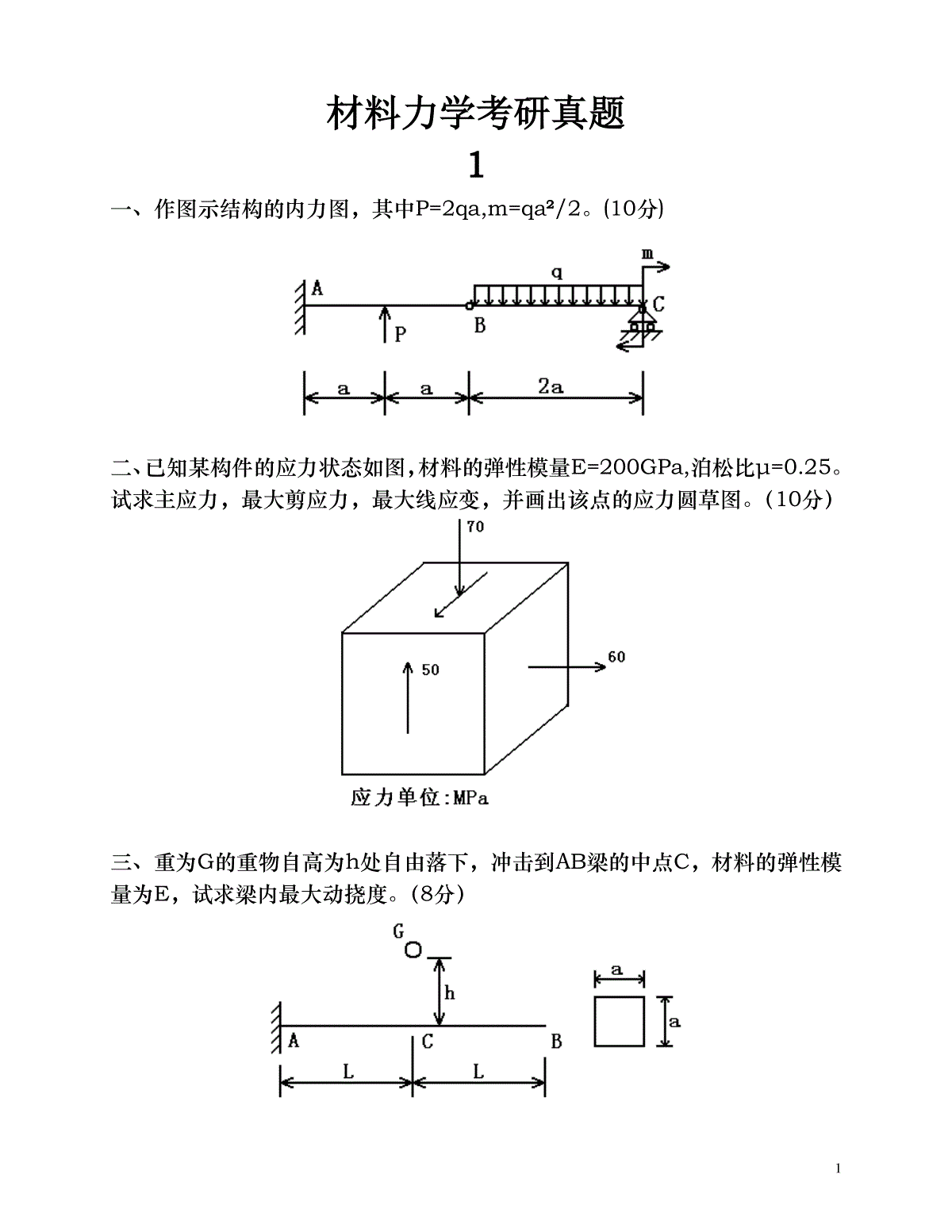
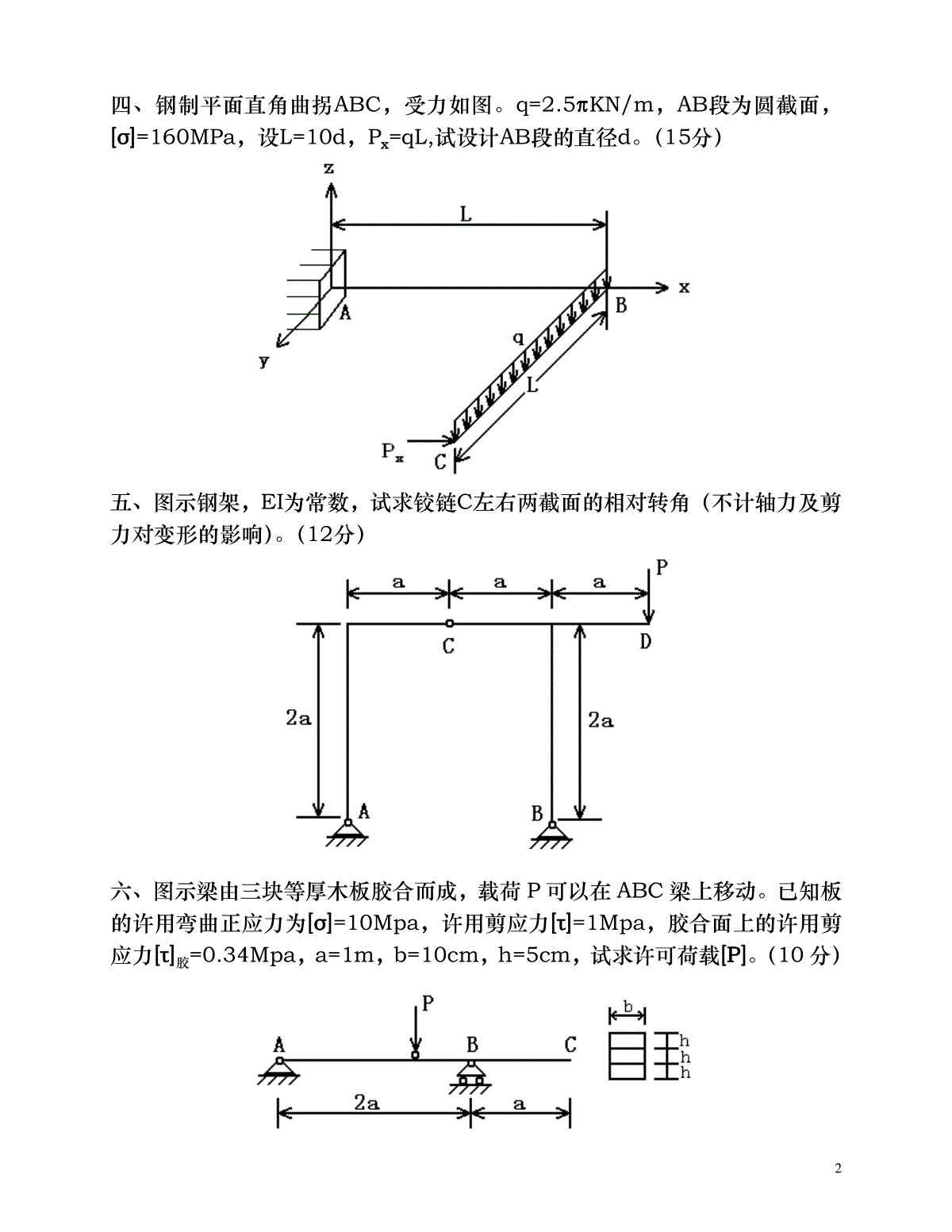
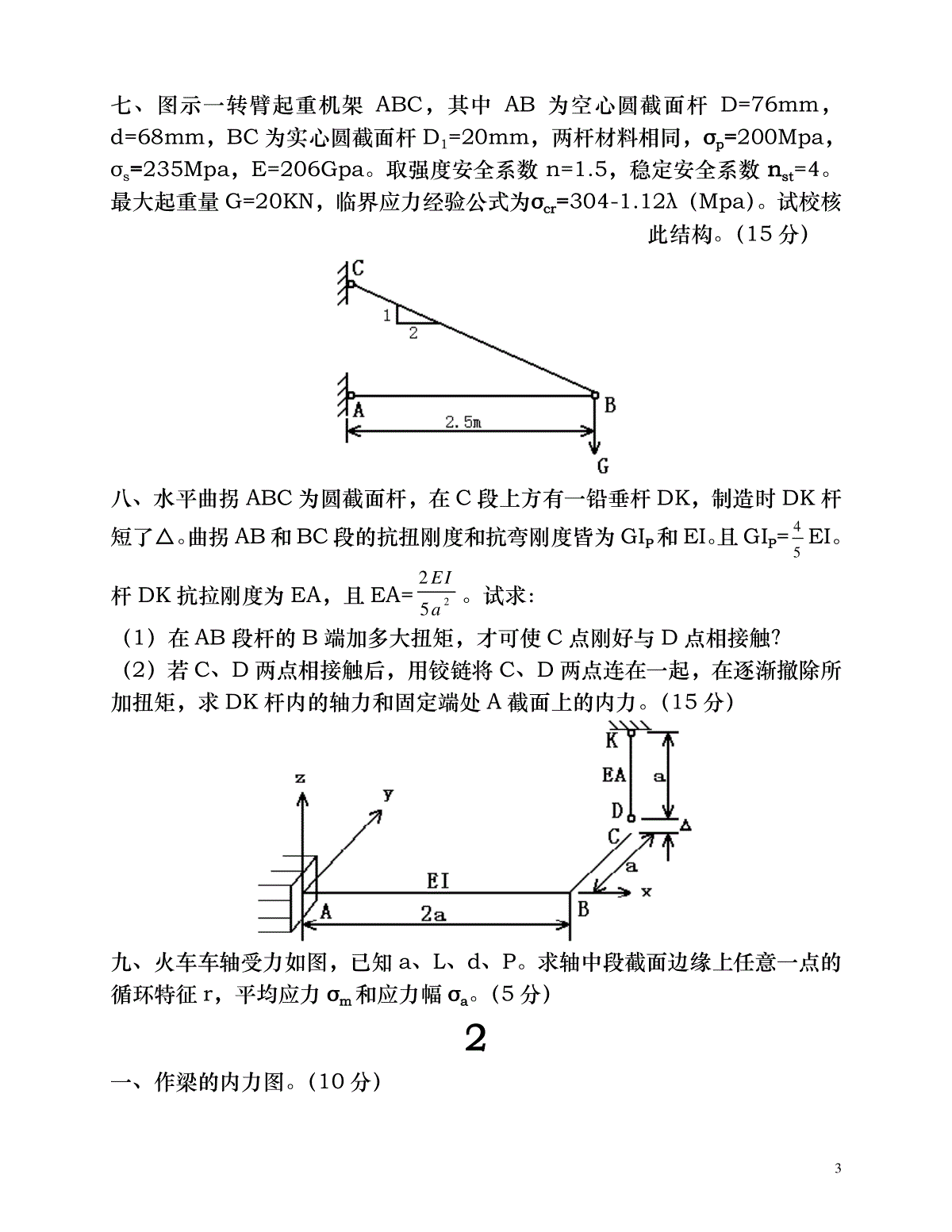
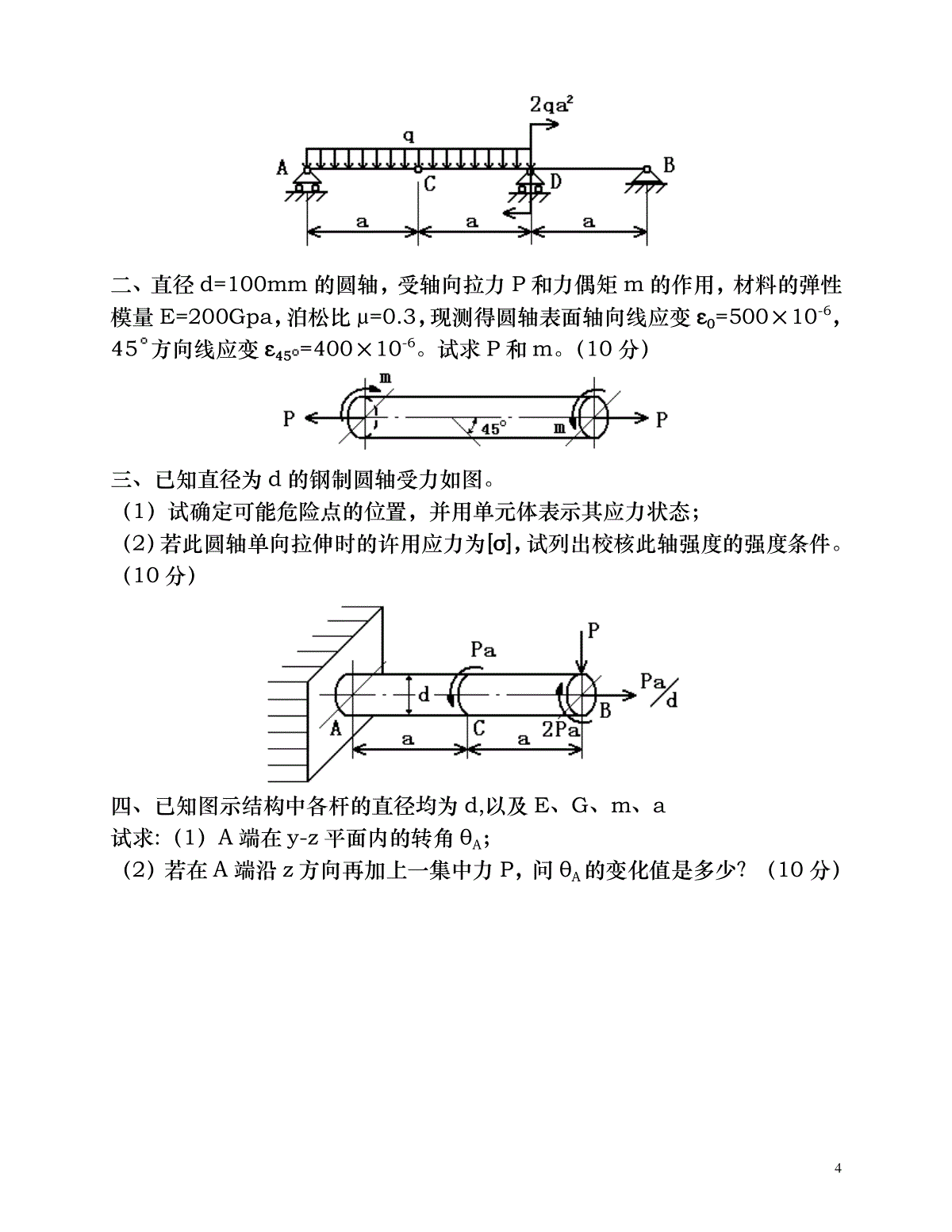
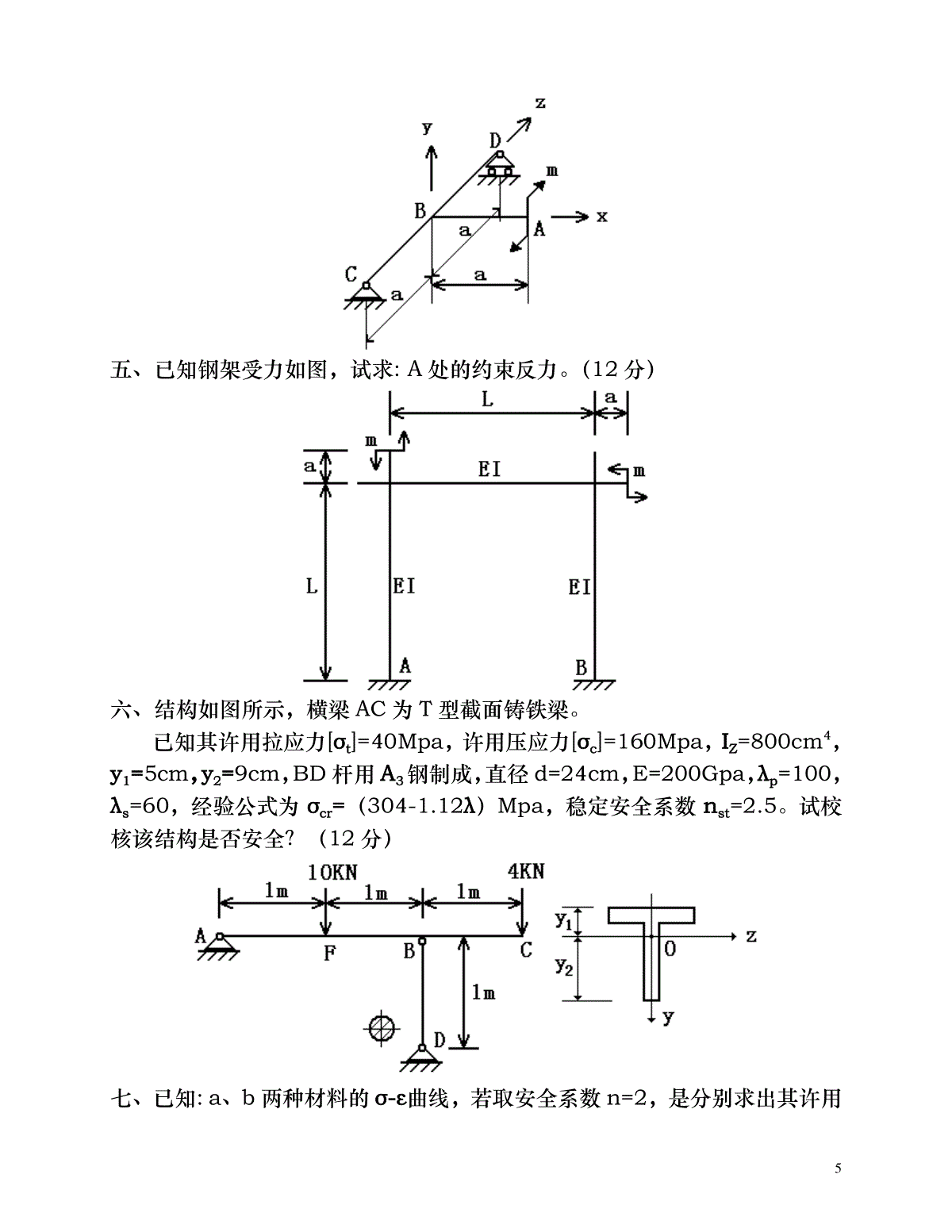
1材料力学考研真题1一、作图示结构的内力图，其中P=2qa,m=qa²/2。(10分)二、已知某构件的应力状态如图，材料的弹性模量E=200GPa,泊松比µ=0.25。试求主应力，最大剪应力，最大线应变，并画出该点的应力圆草图。（10分）三、重为G的重物自高为h处自由落下，冲击到AB梁的中点C，材料的弹性模量为E，试求梁内最大动挠度。（8分）2四、钢制平面直角曲拐ABC，受力如图。q=2.5πKN/m，AB段为圆截面，[σ]=160MPa，设L=10d，Px=qL,试设计AB段的直径d。（15分）五、图示钢架，EI为常数，试求铰链C左右两截面的相对转角（不计轴力及剪力对变形的影响）。（12分）六、图示梁由三块等厚木板胶合而成，载荷P可以在ABC梁上移动。已知板的许用弯曲正应力为[σ]=10Mpa，许用剪应力[τ]=1Mpa，胶合面上的许用剪应力[τ]胶=0.34Mpa，a=1m，b=10cm，h=5cm，试求许可荷载[P]。（10分）3七、图示一转臂起重机架ABC，其中AB为空心圆截面杆D=76mm，d=68mm，BC为实心圆截面杆D1=20mm，两杆材料相同，σp=200Mpa，σs=235Mpa，E=206Gpa。取强度安全系数n=1.5，稳定安全系数nst=4。最大起重量G=20KN，临界应力经验公式为σcr=304-1.12λ（Mpa）。试校核此结构。（15分）八、水平曲拐ABC为圆截面杆，在C段上方有一铅垂杆DK，制造时DK杆短了△。曲拐AB和BC段的抗扭刚度和抗弯刚度皆为GIP和EI。且GIP=45EI。杆DK抗拉刚度为EA，且EA=225EIa。试求：（1）在AB段杆的B端加多大扭矩，才可使C点刚好与D点相接触？（2）若C、D两点相接触后，用铰链将C、D两点连在一起，在逐渐撤除所加扭矩，求DK杆内的轴力和固定端处A截面上的内力。（15分）九、火车车轴受力如图，已知a、L、d、P。求轴中段截面边缘上任意一点的循环特征r，平均应力σm和应力幅σa。（5分）2一、作梁的内力图。（10分）4二、直径d=100mm的圆轴，受轴向拉力P和力偶矩m的作用，材料的弹性模量E=200Gpa，泊松比μ=0.3，现测得圆轴表面轴向线应变ε0=500×10-6，45方向线应变ε45=400×10-6。试求P和m。（10分）三、已知直径为d的钢制圆轴受力如图。（1）试确定可能危险点的位置，并用单元体表示其应力状态；（2）若此圆轴单向拉伸时的许用应力为[σ]，试列出校核此轴强度的强度条件。（10分）四、已知图示结构中各杆的直径均为d,以及E、G、m、a试求:（1）A端在y-z平面内的转角θA；（2）若在A端沿z方向再加上一集中力P，问θA的变化值是多少？（10分）5五、已知钢架受力如图，试求:A处的约束反力。（12分）六、结构如图所示，横梁AC为T型截面铸铁梁。已知其许用拉应力[σt]=40Mpa，许用压应力[σc]=160Mpa，IZ=800cm4，y1=5cm，y2=9cm，BD杆用A3钢制成，直径d=24cm，E=200Gpa，λp=100，λs=60，经验公式为σcr=（304-1.12λ）Mpa，稳定安全系数nst=2.5。试校核该结构是否安全？（12分）七、已知:a、b两种材料的σ-ε曲线，若取安全系数n=2，是分别求出其许用6应力[σ]；并说明何谓冷作硬化现象？（6分）八、已知如图，（1）、试列出求解AB梁弯曲变形所需的挠曲线近似微分方程。（不必积分）（2）、列出确定积分常数所需的全部条件。（6分）九、试指出下面各截面梁在P的作用下，将产生什么变形？（6分）十、求下列结构的弹性变形能。（E、G均为已知）（6分）7十一、已知某材料的σ-1=300Mpa，σb=700Mpa，σ0=450Mpa，用此材料制成的构件的有效应力集中系数Kσ=2.0，尺寸系数εσ=0.8，表面质量系数β=0.9。试作出此构件的持久极限简化折线。（6分）十二、已知如图，一重量为Q的冲击物，以速度v水平冲击杆AB，试根据能量守恒定律，推导水平冲击时的动荷系数。（6分）3一、已知：q、a，试作梁的内力图。（10分）二、图示矩形截面杆，上、下表面的轴向线应变分别为：8εa=1×10-3,εb=0.4×10-3,E=210Gpa1）试求拉力P和偏心距e；2）并画出横截面上的正应力分布图。（10分）三、铸铁梁上作用有可移动的荷载P，已知：y1=52mm，y2=88mm，Iz=763cm4，铸铁拉伸时的σb=120Mpa，压缩时的σb=640Mpa，安全系数n=4。试确定铸铁梁的许可荷载P；并求τmax（10分）四、某低碳钢构件内危险点的应力状态如图，已知：σs=220Mpa，σb=400Mpa，安全系数n=2，E=200Gpa，µ=0.31）试求该点的最大线应变；2）画出该点的应力圆草图；3）并对该点进行强度校核。（10分）五、直径为d的钢制圆轴受力如图。已知：P1=20KN，P2=10KN，m=20KN·m，q=5KN/m，[σ]=160Mpa，试设计AB轴的直径。（10分）9六、已知：q、l、EI试求：等直梁间铰B左右两侧截面的相对转角。（10分）七、圆截面杆AB、BC的直径、材料均相同，已知：p、a，E=2.5G，且CD杆的EA=2EI/5a2，试求：CD杆的内力。（12分）八、已知某合金钢材料的持久极限曲线。试求：1）A、B、C、D各点的循环特征r；2）σ-1和σb；3）G点的σmax和σmin。（8分）10九、图示等截面钢架，受到重量为G=300N的物体冲击，已知：E=200Gpa，试求：钢架内的最大应力。（10分）十、图示正方形桁架，五根杆均为直径d=5cm的圆截面杆，材料为A3钢，E=200Gpa，σp=200Mpa，σs=240Mpa，a=304Mpa，b=1.12Mpa，若取强度安全系数n=2，稳定安全系数nst=3，试确定结构的许可荷载P。（10分）4一、做图示结构中AD段的内力图。（15分）11二、圆轴受弯扭组合变形，m1=m2=150N·m，d=50mm，E=200Gpa，µ=0.3；试画出危险点的应力状态，并求其主应力、最大剪应力、最大线应变值。三、钢制实心圆截面轴AC，[σ]=140Mpa，L=100cm，a=15cm，皮带轮直径D=80cm，重Q=2KN,皮带水平拉力F1=8KN，F2=2KN，试设计AC轴的直径d。（15分）四、矩形截面组合梁，已知材料的弹性模量E、a、b、h，在突加重物Q的作用下，测得中间铰B左、右的相对转角=2，求Q值及梁内横截面上的最大正应力。（15分）五、圆截面平面曲拐OAB与直杆CD直径、材料均相同。已知P、L，且GIp=0.8EI，EA=0.4EI/L2，求O端的约束反力。（20分）12六、矩形截面悬臂梁，已知材料的弹性模量E、L、b、h，在上顶面作用着均布切向荷载q，求轴线上B点的水平位移UB、垂直位移VB、杆件的弹性变形能U。（20分）七、AB为T形截面铸铁梁，已知IZ=4×107mm4，y1=140mm，y2=60mm，许用拉应力[σt]=35Mpa，许用压应力[σc]=140Mpa。CD为圆截面钢杆，直径d=32mm，E=200Gpa，σp=200Mpa，σs=240Mpa，[σ]=120Mpa，nst=3，l=1m，直线经验公式为：σcr=（304-1.12λ）Mpa。当载荷在AB范围内移动时，求此结构的许可荷载[p]。（20分）注：nst为规定的稳定安全系数。八、列出求解AB梁弯曲变形所需的挠曲线近似微分方程（不必积分）；写出确定积分常数所需的全部条件；画出挠曲线的大致形状。已知：q、a、弹簧刚度K，EI为常数。（10分）13九、分别画出低碳钢、铸铁试件在扭转实验中的受力图；将要破坏时横截面上的应力分布图；破环件的断口形式，分析破坏原因。若测得低碳钢破坏时的扭矩为m1，铸铁破坏时的扭矩为m2，写出计算剪切强度极限的表达式（试件直径均为d）。（10分）十、圆轴AB以等角速度ω回转，已知：P、L、d、ω，求危险点的循环特征r；平均应力σm；应力幅σa，画出该点的σ～t曲线。（10分）5一、画图示梁的剪力图和弯矩图。（15分）二、直径为d的钢制圆轴受力如图所示，已知材料的许用应力为[σ]，m=qL2，P=qL，试用第三强度理论设计该圆周的直径d。（15分）三、已知平面曲拐ABC和DF梁的抗弯刚度为EI、抗扭刚度为GIp和CD杆14的抗拉刚度为EA，设EI=4GIP=2EAL2。试求CD杆的内力。（20分）四、结构受力如图所示，横梁AB为T字形截面铸铁梁，已知其许用拉应力为[σt]=40Mpa，许用拉应力为[σc]=160Mpa，Iz=800cm4，y1=50mm，y2=90mm；CD杆用A3钢制成，截面为圆形，d=30mm，E=200Gpa，λp=100，λs=60，经验公式为：σcr=（304-1.12λ）Mpa，稳定安全系数nst=3。试校核该结构是否安全。载荷P可在AB梁上移动。（20分）五、结构受力如图所示，设弹簧刚度为K=5EI/L3，试求C截面的挠度fc。（15分）六、某一钢结构危险点处的应力状态如图所示，已知E=200GPa，μ=0.3，σs=200MPa，σb=400MPa，安全系数n=2。试求：（1）图示单元体的主应力；15（2）最大剪应力；（3）最大线应变；（4）画出相应的三向应力圆草图；（5）对该点进行强度校核。（15分）七、已知某材料的持久极限曲线如图所示，试求（1）A、B、C、D各点的循环特性r；（2）σ-1和σb；（3）G点的σmaz和σmin；（4）画出相应的持久极限曲线的简化折线。（7分）八、结构如图所示，试求结构在静荷载q和动荷载G=qL冲击下D点的挠度fD，设qL4=4hEI，EI为梁的抗弯刚度。（15分）九、圆轴受力如图所示，已知：E=200GPa，μ=0.3，d=100mm，现测得圆轴表面A点沿轴线方向的线应变为ε0°=5×10-4，沿45°方向的线应变为ε45°=4×10-4，试求外荷载P和M。（15分）16十、结构受力如图所示，其中U为结构的弹性变形能，试问的力学意义是什么？十一、一弹性体在广义力P1和P2共同作用下，1、2两点产生的广义位移分别为Δ1和Δ2；设P1单独作用1点时，在1、2两点产生的位移分别为Δ11和Δ21；设P2单独作用2点时，在1、2两点产生的位移分别为Δ12和Δ22。试证明：P1×Δ12=P2×Δ21。（8分）6一、画出图示梁的剪力图和弯矩图。（15分）二、结构受力如图所示，已知平面钢架ABCD的抗弯刚度为EI，EF杆的抗拉刚度为EA，设3EI=EAL2。试求E、F两点的相对位移。（20分）17三、直径为D的钢制圆轴受力如图所示，材料的许用应力为[Σ],已知L、P、M=4PL，试用第三强度理论设计该轴的直径D。（15分）四、已知某钢结构危险点处的应力状态如图所示，E=200GPA，Μ=0.25。试求：（1）图示单元体的主应力；（2）最大剪应力；（3）最大线应变；（4）画出相应的三向应力圆草图。（15分）五、图示为平面直角钢架ABC，受一重物G自高度为H处自由降落在A点处，设EI为钢架的抗弯刚度，试求直角钢架ABC内最大动弯矩MMAX，D。（15分）18六、已知结构某点的交变应力随时间的变化曲线如图所示，试求：（1）循环特性R；（2）平均应力ΣM；（3）应力幅度ΣA；（4）在ΣM—ΣA坐标系中，标出该应力循环对应点，并求出自原点出发且通过该点的射线与水平轴ΣM的夹角Α。（10分）七、一等直杆受轴向拉伸，当应力达到Σ=250MPA时，其应变Ε=2×10-3，已知E=200GPA，L=300MM，试求此杆的塑性应变。（7分）八、图示为一等直杆受偏心拉伸，试确定其任意X截面上的中性轴方程。若设YP=H/6，ZP=B/6，求其中性轴在Y轴和Z轴上的截距（AY=？、AZ=？）各为多少？（8分）197一、画图示梁的剪力图和弯矩图。（15分）二、1、什么是材料的力学性质？2、为什么要研究材料的力学性质？3、今有一新研制的金属（塑性）材