地基承载力计算

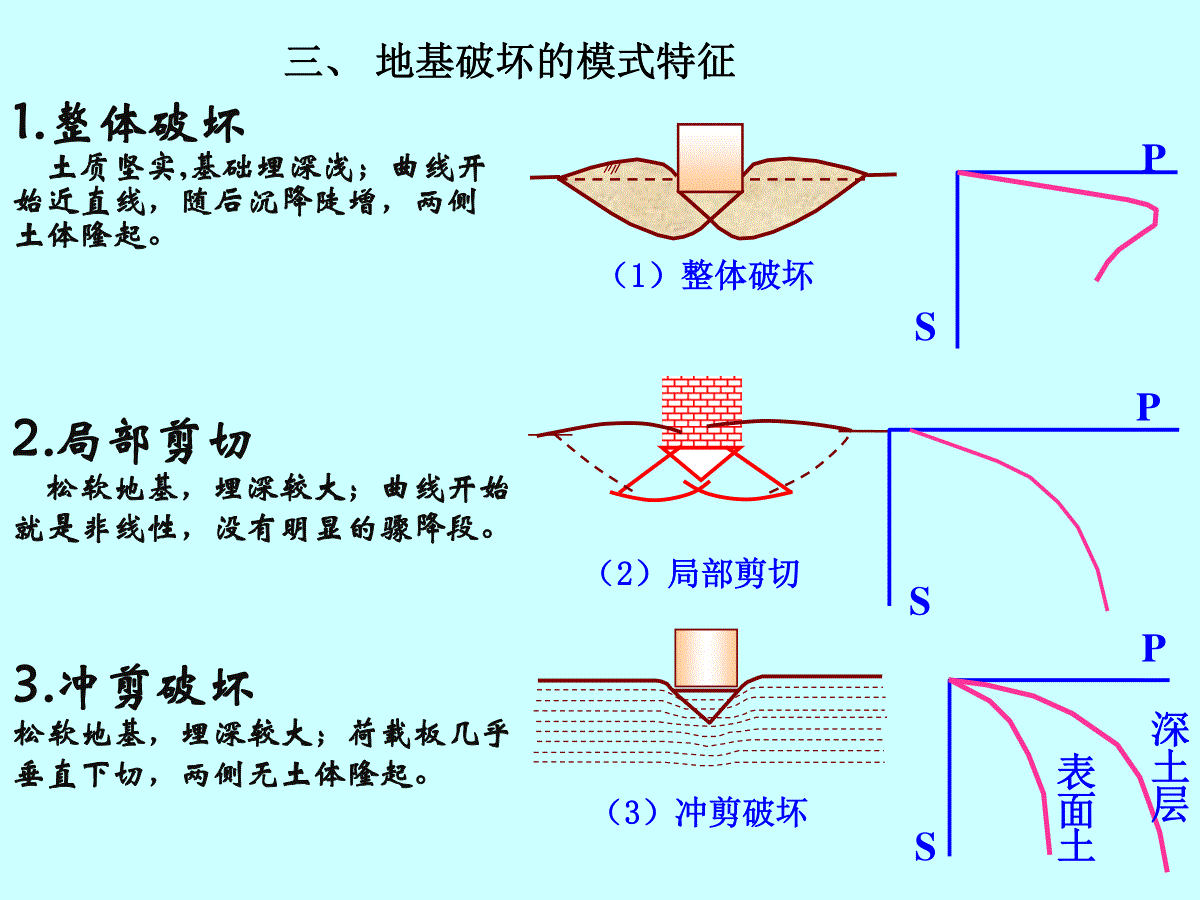
第七章地基承载力计算主要内容：§7.1地基破坏模式§7.2地基的临塑荷载和临界荷载§7.3地基极限承载力的计算§7.4地基承载力公式的适用性一、地基承载力定义•极限承载力承载地基在发生剪切破坏时的荷载强度§7.1地基破坏模式二、地基破坏的模式地基破坏主要是由于基础下持力层抗剪强度不够，土体产生剪切破坏所致，地基的破坏模式可分为：1.整体破坏（密实砂土，坚硬粘土）2.局部剪切破坏（土质较软）3.冲剪破坏（软粘土，深埋）2.局部剪切松软地基，埋深较大；曲线开始就是非线性，没有明显的骤降段。3.冲剪破坏松软地基，埋深较大；荷载板几乎垂直下切，两侧无土体隆起。1.整体破坏土质坚实,基础埋深浅；曲线开始近直线，随后沉降陡增，两侧土体隆起。（1）整体破坏PS（2）局部剪切PS（3）冲剪破坏PS深土层表面土三、地基破坏的模式特征某谷仓的地基整体破坏1940年在软粘土地基上的某水泥仓的倾覆水泥仓地基整体破坏蓝粘土石头和粘土地基土可能的滑动方向岩石办公楼外墙黄粘土在软粘土上的密砂地基的冲剪破坏相邻建筑物施工引起的原有建筑物的局部倾斜（软粘土地基）膨胀土地基上建筑物的开裂（美国—加拿大）潜在性膨胀土的分布限与热带和温带的半干旱地区内。这种条件助长了蒙特石形成。很多国家都发现了膨胀土。印度的黑棉土《膨胀土上的基础》陈孚华TU4431膨胀土对建筑物的危害活动区域一、荷载沉降曲线pcrpupcr~pu临塑荷载连续滑动面和极限荷载塑性区发展和临界荷载pcrpu地基土开始出现剪切破坏s连续滑动面§7.2地基的临塑荷载和临界荷载允许地基中有一定的塑性区，作为设计承载力--考察地基中塑性区的发展•地基土中某一点应力状态：，•极限平衡应力状态（塑性区）sin23131ctgc二、条形荷载塑性区的计算•自重应力：•s1=(d+z)•s3=k0(d+z)•弹性区的附加应力：•合力=1，3•设k0=1.0)2sin2(3,1DpDzM2三、塑性区的计算•弹性区的合力：•极限平衡条件：)()2sin2(3,1zDDpsin23131ctgcDzM2将应力代入极限平衡条件式（2），表示该点既满足弹性区；也满足塑性区—是弹塑像区的边界。在荷载p作用下，得到如下边界方程：z=f()（3）DzM2DctgcDpz)2sin2sin(DctgcDpz)2sin2sin(四、弹塑区边界方程五、塑性区的最大深度zmax塑性区的最大深度Zmax220zDM2DctgcDpz)2sin2sin(•对应Zmax=0—临塑荷载；•Pcr=Nqd+NccNq、Nc承载力系数，可以按照下式进行计算或查表7.1（p161）。NqNcNPcr1+/ctg-/2+)(1-Nq)ctg0各种临界荷载的承载力系数NqNcNPcr1+/ctg-/2+)(1-Nq)ctg01、极限状态结构或结构的一部分超过某一特定状态而不能满足设计规定的某一功能要求时这一特定状态称为结构对于该功能的极限状态2.承载能力极限状态一般是结构的内力超过其承载能力3、正常使用极限状态一般是以结构的变形、裂缝和振动参数超过设计允许的限值为依据根据承载能力极限状态确定地基的承载力§7.3地基极限承载力的计算一、基本概念二、普朗特-瑞斯纳极限承载力公式1、极限平衡理论（1）平衡方程：（2）极限平衡条件（3）假设与边界条件2、普朗特-瑞斯纳承载力公式（1）条形基础地基的滑裂面形状（2）极限承载力puDD3、平面问题的平衡方程xzxzz（1）0zxxzx（2）4、极限平衡条件Sincctg23131（3）zzxxxz5、普朗特(Prandtl)的基本假设1.基础底面是绝对光滑的（，保证竖直荷载是主应力2.无重介质的假设：即在式（1）中=0：根据公式（1）、（2）和（3）以及边界条件，利用塑性力学中的滑移线法可以求解条形基础的地基承载力Pu这一假定下的精确解或解析解.DD6、极限平衡区与滑裂面的形状无重介质地基的滑裂线网BEFBp实际地面DC（1）朗肯主动区：pu为大主应力，与水平方向夹角452（2）过度区：r=r0etg（3）朗肯被动区：水平方向为大主应力，与水平方向夹角45-27、地基中的极限平衡区BEFBp实际地面DCIIIIIIr0r（1）、I区垂直应力pu为大主应力，与水平方向夹角452=pukapuPu（2）III区水平方向为大主应力，与水平方向夹角45-23=D1kpDq=D（3）Ⅲ区：过度区极限平衡第二区：r=r0etgr0r作用在隔离体上的力：pu、D、pa、pp、c、R所有力对A点力矩平衡puR（4）隔离体r0rApppaDcaauaKcKpp2pppKcqKp2r=r0etg=R过顶点Atg=dr/rd=r0etgdtg=r0etgd=tgdRdrdlrd=A+M1：puOA=B/2+M2：paOC=B/2tg(45+/2)-M3:cCE=dl-M4:ppGE=B/2e/2tg-M5:DAG=B/2tg(45+/2)e/2tgpuR隔离体r0rApppaDc8、极限承载力puctgNNtgeNCNDNpqctgqcqu)1()245(2Nq,Nc:承载力系数二、太沙基承载力公式1、基本条件2、假设的滑裂面形状3、极限承载力公式1、基本条件（1）考虑地基土的自重基底土的重量0（2）基底可以是粗糙的0=0(不会超过,为什么?)（3）忽略基底以上部分土本身的阻力,简化为上部均布荷载q=DDmD2、假设的滑裂面形状被动区过渡区刚性核Ep=Ep1+Ep2+Ep3WpuB3、考虑刚性核的平衡(1)当基底绝对粗糙时，夹角为；(2)考虑刚性核的平衡：荷载：pu自重：W粘聚力：C被动土压力EpEp1：土体自重Ep2：滑裂面上粘聚力Ep3：侧向荷载qcuqNcNNBp2232221coscos1cos2pqpcpkNtgkNktgN太沙基公式中的承载力因数N、Nq、Nc查图7.8，以为变量比普朗特-瑞斯纳承载力公式偏大，因为考虑了基底摩擦和土体自重（二）局部剪切破坏（非整体破坏）tg32tgc32c极限承载力pu的组成BN/2cNcDqNq极限承载力的三部分qcqNcNNB2滑动土体自重产生的抗力滑裂面上的粘聚力产生的抗力侧荷载D产生的抗力(1)影响滑裂面形状的大小，承载力因数的大小.滑动土体的体积,q的分布范围,滑裂面的大小.pu(1)的影响pu影响滑裂面形状的大小，承载力因数的大小.滑动土体的体积,q的分布范围,滑裂面的大小.(2)宽度B增加为2B,滑动体体积增加为原来的22倍(提供的抗力),由此增加的承载力增加为原来的2倍.(BN/2线性增加）B增加，q的分布面积线性增加，qNq不变。B增加，滑裂面面积线性增加，cNc不变pupu(3)qNq,与侧面荷载大小，和荷载分布范围有关-滑裂面形状有关。滑裂面形状与有关。Nq,是的函数pupu(4)cNc,与粘聚力，和滑裂面长度有关--滑裂面形状有关。滑裂面形状与有关。Nc,是的涵数pu总结上节课的内容极限承载力理论界和半理论解1Prantl解假设和滑裂面形状2太沙基解，一般解形式3极限承载力的影响因素,c,，D,B,BEFBp实际地面CIIIIIID45o＋/245o－/2qcuqNcNNBp2三、地基的容许承载力1容许承载力f及影响因素fpu/Fs,s[s]特征值fa(设计承载力)2.局部塑性区2地基承受荷载的不同阶段1.弹性阶段-临塑荷载3.极限承载力3、地基承载力设计值f的确定办法：①要求较高：f=Pcr②一般情况下：f=P1/4或P1/3在中国取P1/4或者：③用极限荷载计算：f=Pu/FsFs---安全系数4、确定地基承载力设计值的方法（1）现场试验法：载荷试验、标准贯入试验、静力触探等。要进行修正（2）规范公式计算法，不做宽度深度修正（3）根据经验确定容许承载力，做宽度深度修正5、目前规范中设计承载力的确定（1）静载荷试验fa=fak+b(b-3)+dm(d-0.5)fak:静载荷试验确定的承载力-特征值（标准值）fa：深宽修正后的承载力特征值（设计值）千斤顶荷载板（2）承载力公式法：fa=Mbb+Mdmd+Mcckfa:承载力特征值（设计值）——相当与p1/4=NB/2+Nqd+Ncc但当内摩擦角比较大时，2MbN§7.4地基承载力公式的适用性1、临界荷载和临塑荷载——适用于均布荷载条形基础。2、太沙基承载力公式——适用于基础底面粗糙条形基础且为整体破坏模式。一、各种承载力公式适用条件二、影响极限荷载的因素1、地下水2、地基的破坏模式3、地基土强度指标4、基础设计尺寸5、荷载作用及时间例题分析有一条形基础，宽度b=3m，埋深h=1m，地基土内摩擦角j=30°，黏聚力c=20kPa，天然重度=18kN/m3。试求：（a）地基临塑荷载；（b）当极限平衡区最大深度达到0.3b时的均布荷载数值。解：（a）计算公式：时，有：化简后，得到：p0.3b=333.8kPa（b）临界荷载：