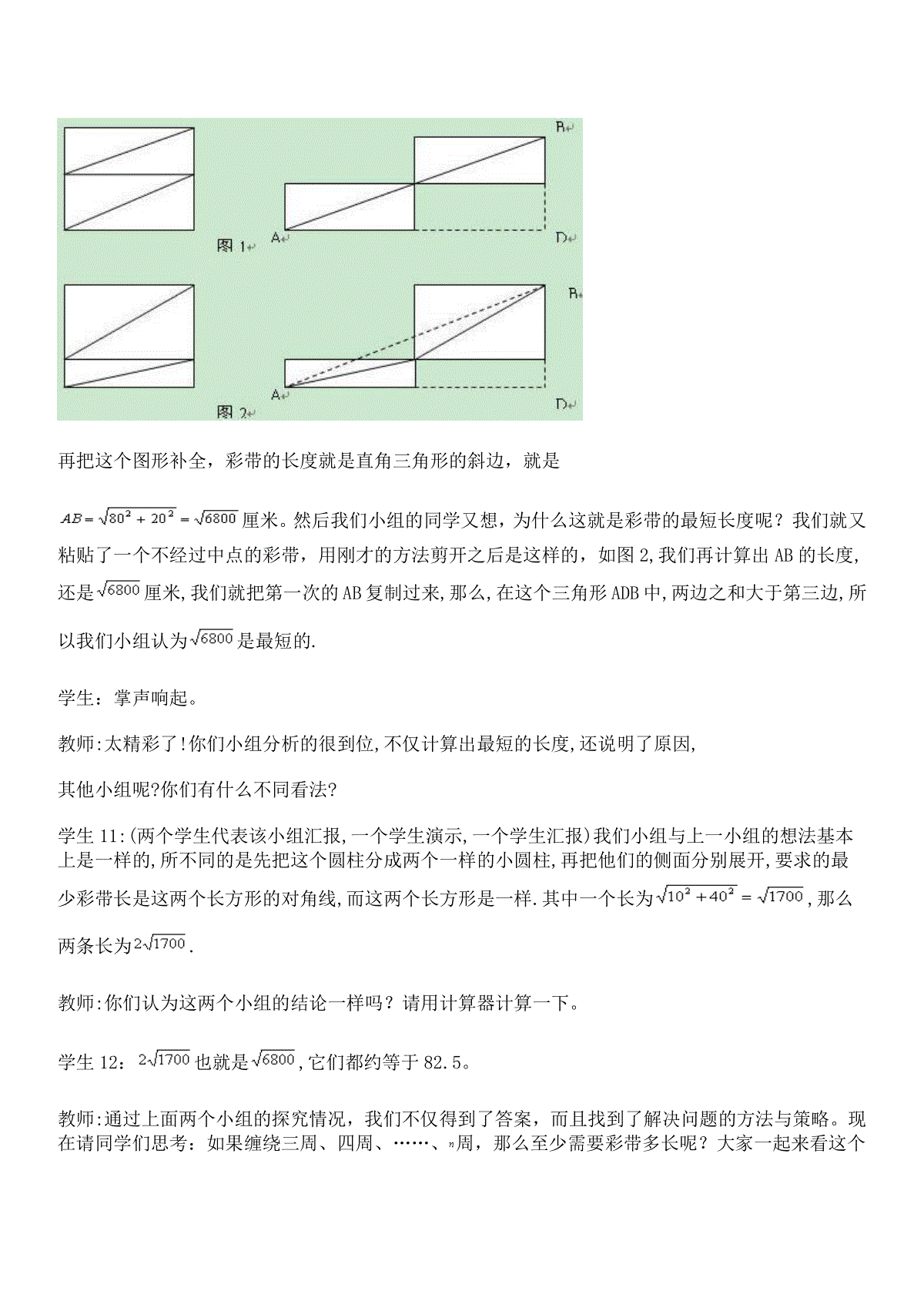
勾股定理应用的探究

《勾股定理应用的探究》教学实录与评析做课教师：大连理工大学附属学校/郑晓玮评课教师：大连教育学院初中教师教育中心数学研训教师/金晔背景情况介绍：第十三届东北三省四城市数学青年教师教学研讨会于10月19日在大连理工附属学校召开，以探究式教学为主题，来自大连、沈阳、长春、哈尔滨四城市的四位青年教师分别做课、研讨、交流。下面是大连选手做的《勾股定理应用的探究》教学实录。教学实录教师：上课！同学们好！学生：老师好！教师：前面我们已经学习了勾股定理，并且利用勾股定理解决了一些简单的实际问题，今天这节课我们将以前面研究过的两道例题为基础进一步探究勾股定理的应用。教师：板书课题《勾股定理的应用》。教师：首先，大家一起来回顾第一个例题，并回忆一下，你是如何求出点A与地面距离的？教师：演示第一个例题：（华师版八上50页例1）如图，将长为5.41米的梯子AC斜靠在竖直的墙上，BC的长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)学生1：这个问题中，我们知道墙面和地面是互相垂直的，根据勾股定理在直角三角形ABC中，，知道梯子AC的长度和BC的长度，，我们就能求出A点距离地面的高度了。教师：很好，勾股定理运用的非常熟练。那么大家能不能利用勾股定理解决今天的新问题呢？教师演示新问题：如图，将长2.5米的梯子AC斜靠在竖直的墙上,梯子底端C与墙的水平距离BC的长为1.5米,若梯子底端点C在水平方向向后移动了0.5米,它的上端点A在竖直方向下滑了多少米?教师：请大家独立思考并完成。学生：学生独立思考并解决问题，学生2板书过程。教师：请学生2把解决这个问题的思路讲给大家听一听。学生2：这个问题是要求AA′的长度，在ABC中，根据勾股定理，可求=2，在中，根据勾股定理，可求，所以。教师：请同学们评价一下。学生3：板书工整，思路清晰！除了单位没写，没有其他问题。教师：得到答案是0.5米的同学请举手？（个别学生没有举手）教师：解决这个问题的关键在于明确墙面与地面始终垂直，梯子的滑动的过程当中长度始终不变，滑动前后分别在两个直角三角形中，利用勾股定理便可将问题解决。请大家注意观察，如果线段CC′等于0.6米，你认为线段AA′的长度是多少呢？部分学生：0.6米。部分学生：不一定。（小部分学生沉默）教师：回答是0.6米的同学，请你说一说，你的依据是什么呢？（学生举手）学生4：我认为梯子下端移动的距离与上端下滑的距离相等。教师：都同意这个结论？请你们猜想并探究你的结论。（3分钟）教师：现在以小组为单位，一起探究，五分钟以后，比一比哪个小组的方法又多又好？教师：请大家坐好，哪个小组先来说说你们讨论的结果？学生5：我们小组的想法是假设AA′和CC′都是0.6米,A′B的长度为(2-0.6)米，,,所以根据勾股定理的逆定理,这就不是一个直角三角形,而我们知道墙与地面始终是互相垂直的,这个三角形一定是直角三角形,所以我们小组认为这两条线段不一定相等.学生6：我们小组先假设米,通过计算米，所以我们也认为这个结论是错误的.学生7：我们小组是假设米，通过计算发现米，所以我们也认为这个结论是不正确的。教师：学生7与学生6方法和上一个小组是一样的，只是假设的数据不同，非常好。学生8：我们小组是设，则。设下端后移了x米，上端下滑了y米，则只有当的时候才能使，所以这两条线段不一定相等。教师：这个小组给大家提供了一种更一般的说明问题的方法,思维很有创新性，实在是太棒了,大家一起给这个非常有创意的方法一些掌声吧!学生：掌声！（情不自禁的）教师:我们刚才用不同的方法说明了这个结论是不正确的。其实要说明一个结论是不正确，只要举出一个反例就可以了！通常也是最简单的方法。教师：到此，我们对例题一的拓展探究告一段落，下面，大家一起回顾一下第二个例题。教师:演示第二个例题：（华师版八上57页例1）一个圆柱体的地面周长为20cm，高AB为4cm，BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，试求出爬行的最短路程。教师：请大家回忆一下，我们是如何求出蚂蚁爬行的最短距离的？学生8：我们是把这个圆柱的侧面展开后，在平面内，利用勾股定理求点A和点C间的线段长，即可得到蚂蚁爬行的最短距离。教师：现在将上面的问题情境变化一下,那么该如何解决下面这个新问题呢？教师：演示活动2内容：有一个圆柱体礼盒，高为20厘米，底面为周长40厘米，准备在礼盒表面粘贴彩带作为装饰，若彩带一端粘在点A处,另一端绕礼盒侧面一周后粘贴在点B处，你认为至少需要彩带多长呢？学生9：与例二的解题思路一样，先把圆柱的侧面展开，然后再平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离。在直角三角形中，一条直角边长等于圆柱的高，另一条直角边长等于底面周长，利用勾股定理，可求得。教师:为什么厘米是最短的?学生齐答:两点之间线段最段.教师:现在用一根彩带在圆柱体礼盒上缠绕两周，那么你认为最少需要彩带多长呢?教师:演示活动三:有一个圆柱体礼盒，高为20厘米，底面为周长40厘米，准备在礼盒表面粘贴彩带作为装饰，彩带一端粘在点A处，另一端绕礼盒侧面两周后粘贴在点B处,你认为至少需要彩带多长呢？教师:请大家先独立思考，再以小组为单位,利用手中的模型,探究活动三中最少需要彩带多长?学生：以小组为单位交流讨论。（5分钟）教师：哪个小组先来汇报你们探究的结果？学生10：（两个学生代表该小组汇报，一个学生演示，一个学生讲解）我们小组最开始直观感觉当彩带经过圆柱高的中点的时候是最短的，按照这种缠绕方法进行粘贴，然后把这个圆柱展开，发现要求的彩带是两个一样的长方形的对角线，于是我们把侧面又裁成两个小长方形，再把其中一个小长方形移到这个如图1位置，再把这个图形补全，彩带的长度就是直角三角形的斜边，就是厘米。然后我们小组的同学又想，为什么这就是彩带的最短长度呢？我们就又粘贴了一个不经过中点的彩带，用刚才的方法剪开之后是这样的，如图2,我们再计算出AB的长度,还是厘米,我们就把第一次的AB复制过来,那么,在这个三角形ADB中,两边之和大于第三边,所以我们小组认为是最短的.学生：掌声响起。教师:太精彩了!你们小组分析的很到位,不仅计算出最短的长度,还说明了原因,其他小组呢?你们有什么不同看法?学生11:(两个学生代表该小组汇报,一个学生演示,一个学生汇报)我们小组与上一小组的想法基本上是一样的,所不同的是先把这个圆柱分成两个一样的小圆柱,再把他们的侧面分别展开,要求的最少彩带长是这两个长方形的对角线,而这两个长方形是一样.其中一个长为,那么两条长为.教师:你们认为这两个小组的结论一样吗？请用计算器计算一下。学生12：也就是,它们都约等于82.5。教师:通过上面两个小组的探究情况，我们不仅得到了答案，而且找到了解决问题的方法与策略。现在请同学们思考：如果缠绕三周、四周、……、周，那么至少需要彩带多长呢？大家一起来看这个思考题。教师:演示思考题内容:“另一端绕礼盒侧面两周后粘在点B处”，改为“另一端绕礼盒侧面三周后粘在点B处”，至少需要多长的彩带？改为绕四周、绕五周、……、绕n周呢？学生:看题并思考.教师:先独立思考，然后小组交流.教师:哪个小组能让我们分享你们的探究成果?学生13:我们小组。按照活动二和活动三解决问题的方法展开圆柱、裁剪、拼接如下图，我们不难发现，绕一周时候水平的直角边长是40厘米,绕两周时候水平的直角边长是80厘米,绕三周时候水平的直角边长是120厘米,绕四周时候水平的直角边长应该是四个圆柱体的底面周长,依次类推,绕n周时候水平的直角边长就应该是n个底面周长,也就是40n厘米,而直角三角形的高始终是20厘米.所以根据勾股定理彩带长就是厘米.学生14:我们小组是这样计算的,把侧面分成n个小长方形,每个宽为厘米,长都是40厘米,根据勾股定理计算出彩带长为教师:这两个小组的方法是以刚才两组的两种方法为基础,探究出结论的,思路都非常清晰.我们现在通过实际操作，探究出了解决这个问题的方法，有了这个方法，无论是把彩带缠绕几周，我们都能够求出圆柱体需要彩带的最短长度。教师：现在大家一起来回顾这节课的内容，想一想你都有哪些收获？学生15：通过梯子下滑的问题，我知道了仅仅看到事物的表面还不能盲目的下结论，需要在实践中验证自己的判断。学生16：我学会了说明一个结论不正确的方法：举反例等。学生17：我会利用勾股定理解决实际生活问题了。学生18：我知道了在解立体图形中的问题时，可以将立体图形问题转化为平面问题。学生19：已知直角三角形的两边，利用勾股定理可求第三边。教师：看来这节课大家收获颇多，我们再回到粘贴彩带的问题中来，想一想，如果要在如图所示的正方体和长方体礼盒上粘贴彩带，把彩带一端粘贴在点A处，另一端粘贴在点B处，你们又如何求解上面的问题呢？教师：演示课后思考：如果要在如图所示的正方体和长方体礼盒上粘贴彩带，把彩带一端粘贴在点A处，另一端粘贴在点B处，如何求出至少需要多长的彩带？教师：请同学们课后探究。教师：这节课就到这，下课，同学们再见！学生：老师再见！对本节课的评析：我个人认为，这节课的特点是设计起点高、探究性强、实施难度大、教学价值高，是一节成功的探究课。具体体现在以下四个方面：第一、这节课较好地体现了新课程理念。从教学设计到教学实施都立足于学生，从学生的生活经验、学习经验及实际情况出发，特别是在内容安排和问题设计上，教师做到了“以生为本”，关注学生学习的起跳点、关注学生学习的需求点、关注学生学习的优势点。这节课学生学习的起跳点就是勾股定理简单的应用，这节课学生的需求点就是学生的探究欲望，这节课学生的优势点就是大连理工附中学生较高的思维水平。从梯子滑动问题与粘贴彩带问题的设计来看，充分体现了教师重视数学知识的应用、重视对学生应用数学意识的培养。从教学实施情况来看，教师注重过程性教学，并将知识、技能、思想、方法、策略全部蕴于教学过程之中。另外，教师根据教学内容恰当地选择了教学方式，做到突出探究式教学，兼顾讲授式教学，教学实施过程比较自然合理。应该说，新课程理念在这节课上得到了较充分的体现。第二、从教学设计上看，具有生成性，体现了教学创新的意识。这节课是在华师大版八年级上册第十三章勾股定理新授课全部结束的基础上设计的一节探究课。对勾股定理这一章来说，从课标要求到教材内容设置起点都比较低----一方面表现在知识点少即仅有勾股定理及勾股定理逆定理两个知识点、另一方面表现在能力要求单一即运用勾股定理解决简单的实际问题。教师在没有现成、固定的教学内容情况下，设计一节探究课确实是一件比较困难的事。年轻的郑老师能知难而上，深入研究课标、反复研读教材，根据学生实际情况，利用教材资源和学生的智慧资源开发出这节课的教学内容，具体来说，活动一和活动二是对教材中例题的继续与延伸，“对梯子两端点滑动距离间关系的探究”和活动三对教材中例题的拓展与深化，做到了依靠教材又超越教材。特别是这两个问题都具有一定的探究价值，有助于学生质疑、发现、解决问题等能力的提高。总之，这节课的内容具有生成性和创造性。第三、从教学实施过程来看，较好地发挥了学生的主体作用，教师的主导作用。这节课的活动模式是：先回顾教材上的原问题----然后对原问题延伸----再生成新问题----探究新问题，以这样一个活动主线展开教学过程。在每个活动环节中，特别是在学生探究解决问题方案的过程中，教师能走进学生，与学生一起讨论、交流，发现并收集学生在活动中所遇到的对问题认识的疑点、处理问题的难点、解决问题的亮点。具体表现在：说明梯子两端点移动距离之间的关系时，学生用了三种方法：第一种是特殊值法，学生分别取梯子上端点向下滑动0.6cm、0.7cm等情况进行探究；第二种是极端值法，假设梯纸上端点向下滑动2cm或0cm时进行探究；第三种是假设比较法，假设梯子两端点移动的距离相等，通过比较与梯子的长进行探究。在教师不仅发挥了一个组织者、引领者的作用，同时发挥了一个参与者与合作者的作用。学生作为活动的主体，由于有充分的独立思考时间，学生的各种思维也被有效激活，为合作交流奠定了有利基础。特