搜索
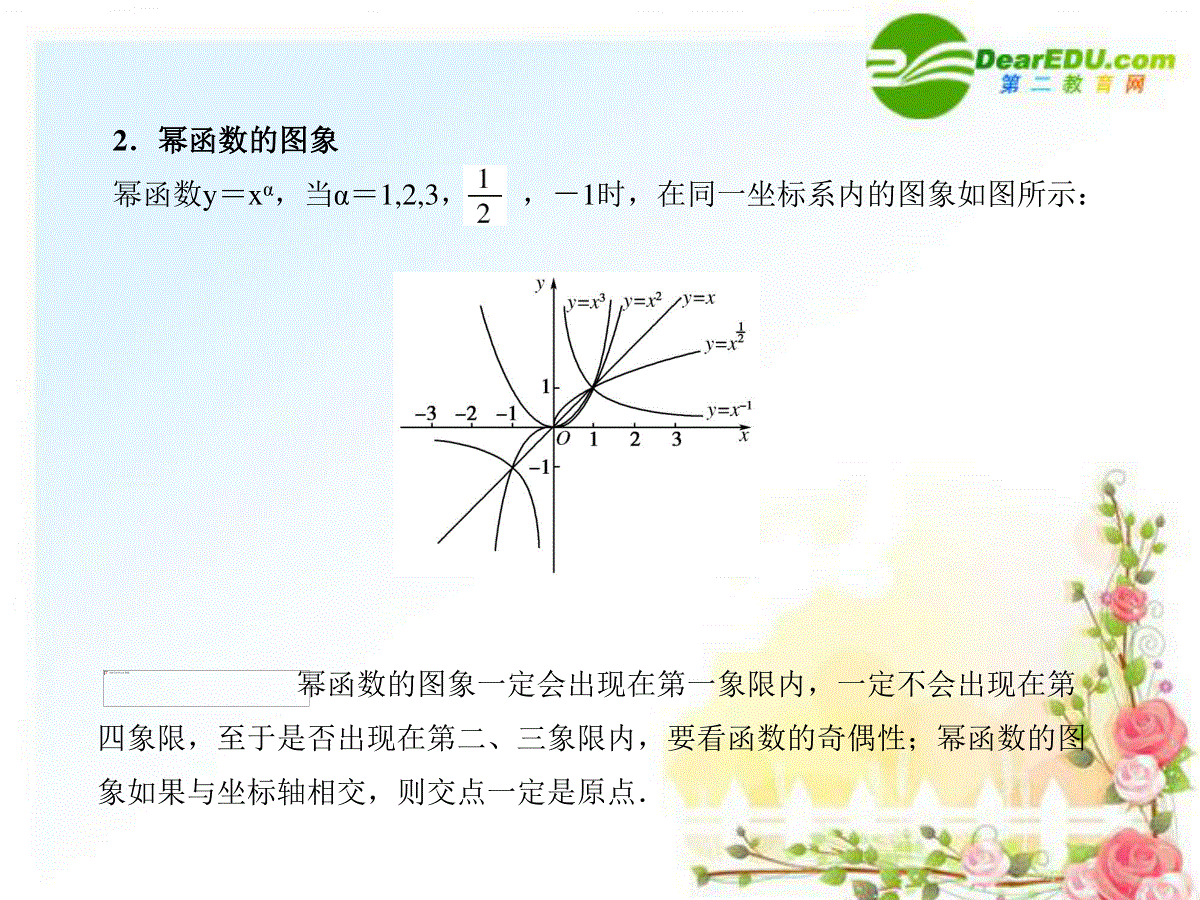
第七节幂函数1．幂函数的定义形如y＝xα(α∈R)的函数称为幂函数，其中x是自变量，α为常数．2．幂函数的图象幂函数y＝xα，当α＝1,2,3，，－1时，在同一坐标系内的图象如图所示：幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象如果与坐标轴相交，则交点一定是原点．3．幂函数的性质(1)在(0,1)上，幂函数中指数越大，函数图象越靠近x轴，在(1，＋∞)上，幂函数中指数越大，函数图象越远离x轴．(2)当α＞0时，幂函数y＝xα在(0，＋∞)上是增函数．当α＜0时，幂函数y＝xα在(0，＋∞)上是减函数．(3)幂函数中既有奇函数，又有偶函数，也有非奇非偶函数．1．下列函数：①y＝；②y＝3x－2；③y＝x4＋x2；④y＝，其中幂函数的个数为()A．1B．2C．3D．4【解析】∵①中y＝x－3；④中y＝适合幂函数定义；而②中y＝3x－2，③中y＝x4＋x2不符合幂函数的定义．【答案】B2．设α∈，则使函数y＝xα的定义域为R且为奇函数的所有α值为()A．1,3B．－1,1C．－1,3D．－1,1,3【解析】∵y＝x－1的定义域为(－∞，0)∪(0，＋∞)，∴α＝－1不合题意．排除B、C、D，故选A.【答案】A－1，1，12，33．已知点M33，33在幂函数f(x)的图象上，则f(x)的表达式为()A．f(x)＝x3B．f(x)＝x－3C．f(x)＝x12D．f(x)＝x－12【解析】设f(x)＝xα，则3＝，所以α＝－3，即f(x)＝x－3.【答案】B【解析】f(f(f(0)))＝f(f(－2))＝f(1)＝1.【答案】15．函数y＝xa，y＝xb，y＝xc的图象如右图，则实数a、b、c的大小关系为.【解析】由图可知三图象的交点为(1,1)，过x＞1的某一点(x0,0)，作直线x=x0，与y=xa，y=xb，y=xc交于三点(x0，x0a)，(x0，x0b)，(x0，x0c)，其中纵坐标大的对应其幂指数值也大，∴a＞b＞c.【答案】a＞b＞c已知函数f(x)＝(m2－m－1)x－5m－3，m为何值时，f(x)：(1)是幂函数；(2)是幂函数，且是(0，＋∞)上的增函数；(3)是正比例函数；【思路点拨】(1)(3)分别利用相应函数的定义确定m的值，(2)中利用幂函数的性质与幂指数之间关系，确定m.【解析】(1)∵f(x)是幂函数，故m2－m－1＝1，即m2－m－2＝0，解得m＝2或m＝－1.(2)若是幂函数且又是(0，＋∞)上的增函数，则－5m－3＞0，即m＜－，∴m＝2(舍去)，故m＝－1.(3)若f(x)是正比例函数，则－5m－3＝1，解得m＝－，此时m2－m－1≠0，故m＝－.比较下列各题中两个值的大小．(1)30.8,30.7；(2)0.213,0.233；(3)212，1.813.【解析】(1)函数y＝3x是增函数，∴30.8＞30.7.(2)函数y＝x3是增函数，∴0.213＜0.233.(3)∵212＞1.812＞1.813，∴212＞1.813.比较两个幂的大小关键是搞清楚是底数相同，还是指数相同，若底数相同，利用指数函数的性质；若指数相同，利用幂函数的性质；若底数、指数皆不相同，考虑用中间值法．【解析】(1)函数y＝x在(0，＋∞)上为减函数，又3＜3.1，∴3＞3.1.已知幂函数f(x)＝x(m2＋m)－1(m∈N)(1)试确定该函数的定义域，并指明该函数在其定义域上的单调性；(2)若该函数还经过点(2，)，试确定m的值，并求满足条件f(2－a)＞f(a－1)的实数a的取值范围．【解析】(1)∵m2＋m＝m(m＋1)，m∈N，而m与m＋1中必有一个为偶数，∴m2＋m为偶数．∴函数f(x)＝x(m2＋m)－1(m∈N)的定义域为[0，＋∞)，并且函数f(x)在其定义域上为增函数．解决此题的突破口在于挖掘出隐含条件m2＋m为偶数．第(2)问求实数a的取值范围时，一定要保证式子f(2－a)和f(a－1)有意义．【解析】设f(x)＝xα，因为点(2，2)在f(x)的图象上，所以(2)α＝2，所以α＝2，即f(x)＝x2；又设g(x)＝xβ，因为点2，12在g(x)的图象上，所以2β＝12，所以β＝－1，即g(x)＝x－1.在同一坐标系下画出函数f(x)和g(x)的图象，如图则有：h(x)＝x－1，x＜0x2，0≤x≤1.x－1，x＞1根据图象可知函数h(x)的最大值等于1，单调递增区间是[0,1]；单调递减区间是(－∞，0)、(1，＋∞)．曾经被削弱地位的幂函数在新课标教材中，又有所加强，幂函数与指数函数有着密不可分的联系，学习幂函数对揭示三次函数和分式函数等的规律也有着重要的作用．高考中，对幂函数的考查多以选择、填空题的形式出现，其难度较低．1．已知幂函数f(x)＝xα的部分对应值如下表：则不等式f(|x|)≤2的解集是()A．{x|－4≤x≤4}B．{x|0≤x≤4}C．{x|－2≤x≤2}D．{x|0＜x≤2}【解析】由表知22＝(12)α，∴α＝12，∴f(x)＝x12.∴(|x|)12≤2，即|x|≤4，故－4≤x≤4.故选A.【答案】A2．下列函数中，既是偶函数又在(0，＋∞)上单调递增的是()A．y＝x3B．y＝cosxC．y＝D．y＝ln|x|【解析】y＝x3是奇函数，排除A选项；y＝cosx在(0，＋∞)不单调，排除B；y＝x－2在(0，＋∞)单调递减，排除C.故选D.【答案】D课时作业点击进入链接