大学课件 高等数学 对面积的曲面积分

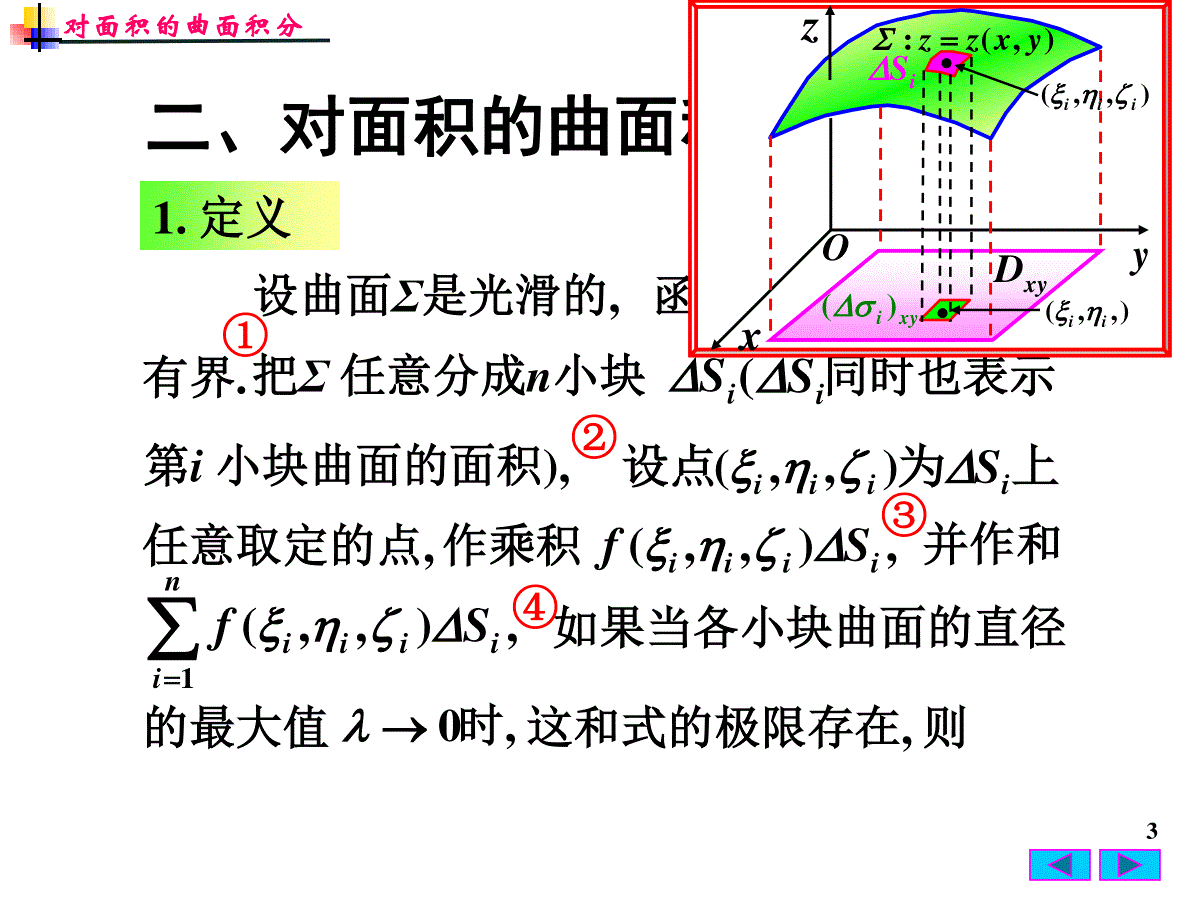
1第四节对面积的曲面积分surfaceintegral第十章曲线积分与曲面积分概念的引入对面积的曲面积分的定义对面积的曲面积分的计算法小结思考题作业2实例解第一步:将Σ分为许多极其微小的子域,以dS为代表,dS的质量为:MMd第二步:求和取极限SzyxMd),,(则Szyxd),,(,d),,(Szyx取所谓曲面光滑即曲面上各点处都有切平面,且当点在曲面上连续移动时,切平面也连续转动.光滑的,是若曲面它的面密度为连续函数),,,(zyx求它的质量.对面积的曲面积分一、概念的引入31.定义iS(上为设点iiiiS),,(,),,(iiiiSf,),,(1iiiniiSf,0时iS函数f(x,y,z)在Σ上任意取定的点,并作和如果当各小块曲面的直径这和式的极限存在,则的最大值①②③④对面积的曲面积分二、对面积的曲面积分的定义第i小块曲面的面积),作乘积设曲面Σ是光滑的,同时也表示有界.把Σ任意分成n小块xyOz),(:yxzz),,(iii),,(iiiSxyDxyi)(4在),,(zyxf或.d),,(Szyxf记为即如曲面是曲面元素被积函数则积分号写成iiiniiSf),,(lim10Szyxfd),,(积分曲面iiiniiSf),,(1称极限为函数上在曲面对面积的曲面积分第一类曲面积分.闭曲面,对面积的曲面积分5则及可分为分片光滑的曲面若,212.存在条件在光滑曲面Σ上今后,假定12(,,)d(,,)dfxyzSfxyzSSzyxfd),,(的曲面积分存在.对面积连续,),,(zyxf当.),,(上连续在zyxf对面积的曲面积分3.对面积的曲面积分的性质6补充设分片光滑的Szyxfd),,(x的奇函数x的偶函数.d),,(21Szyxf.0),(:1zyxx其中,0则曲面Σ关于yOz面对称,为当),,(zyxf为当),,(zyxf对面积的曲面积分74.对面积的曲面积分的几何意义空间曲面Σ的面积:SAd1d122Dyxzz5.对面积的曲面积分的物理意义面密度为连续函数;d),,(SzyxM时，当1),,(zyxf的质量M为:的光滑曲面),,(zyx对面积的曲面积分其质心坐标为:,d),,(1SzyxxMx,d),,(1SzyxyMy.d),,(1SzyxzMz8],,[yxfSzyxfd),,(:若曲面则按照曲面的不同情况分为以下三种：思想是:yxzzSyxdd1d22化为二重积分计算.),(yxzyxzzyxdd122xyD),(yxzz(1)对面积的曲面积分三、对面积的曲面积分的计算法922[,,]1ddxzfxzyyxzSzyxfd),,(则],,[zyfSzyxfd),,(：若曲面则xzDyzD),(zyxzyxxzydd122(2)(3)),(zyxx对面积的曲面积分(,)yxz:(,)yyxz若曲面10确定投影域并写出然后算出曲面面积元素;最后将曲面方程代入被积函数,对面积的曲面积分时,首先应根据化为二曲面Σ选好投影面,曲面Σ的方程,重积分进行计算.对面积的曲面积分11xyzO例解yz5投影域:}25|),{(22yxyxDxy5,d)(zySzyx为平面其中计算2522yx被柱面所截得的部分.:曲面Szyxd)(xyDy52yxdd故)(yxyxzzSyxdd1d22对面积的曲面积分xyDyxxdd)5(22125二重积分的对称性xyDyxdd52对称性2ddxy12解依对称性知成立1422yxz||xyz.为偶函数、关于xy,d||Sxyz计算).10(22zyxz为抛物面其中例面均对称；面、关于yOzxOz抛物面有对面积的曲面积分被积函数1为第一卦限部分曲面.xyzO13yxyxSdd)2()2(1d22Sxyzd41xy4极坐标d41sincosd41022220xyD)(22yxyxyxdd)2()2(122Sxyzd||投影域：}0,0,1|),{(22yxyxyxDxyd41d2sin2210502uuud)41(4125142015125u对面积的曲面积分22:(01)zxyz14例所围成的空间立体的表面.,dSx计算,122yx是圆柱面其中02zxz及平面对面积的曲面积分zxyOzxyOzxyO15解2dSx1231dSxDyxxdd0Dyxxdd1100z2xz122yx投影域1:22yxD对面积的曲面积分例所围成的空间立体的表面.,dSx计算,122yx是圆柱面其中02zxz及平面对称性zxyO16zxyO(左右两片投影相同)zxyySzxdd1d22zxxdd112Sxd1:223yx将投影域选在面上xOz注21xy分成左、右两片3dSxSxd31Sxd32312x2xzDzxxdd112对面积的曲面积分zxxxdd122012x12xzSxd00对称性xzO1117zxyO计算曲面积分SzyxId)(222其中Σ是球面.2222azzyx)0(a解Σ的方程方程是:222yxaaz方程是:投影域222:ayxDxyΣ222yxaaz记上半球面为,1下半球面为,2不是单值的.的值.对面积的曲面积分18对上半球yxzzSyxdd1d22yxyxaadd222得1d)(222Szyx对下半球2d)(222Szyxyxyxayxaaadd)(22222222222:ayxDxyxyDxyDazzyx2222Σ是球面yxyxayxaaadd)(22222222222yxaaz222yxaaz对面积的曲面积分19所以aaa022203dd4极坐标I122223dd4yxayxa48ayxyxayxaaadd)(22222222yxyxayxaaadd)(22222222xyDxyDxyD222:ayxDxy对面积的曲面积分20zxyO计算,d)(23Szyxx其中Σ为球面222yxaz之位于平面曲面Σ的方程Σ在xOy面上的投影域2222:hayxDxyΣ解222yxaz2222:hayxDxy)0(ahhz上方的部分.对面积的曲面积分21zxyOΣ2222:hayxDxy因曲面Σ于是)(22haaSzd00222yxayxyxaadd222x3是x的奇函数，x2y是y的奇函数.Szyxxd)(23222yxazxyD关于yOz面及xOz面对称;对面积的曲面积分22222d1ddddxyaSzzxyxyaxy22例,d2Sx求2222:azyx解积分曲面方程轮换对称Szyxd)(222SzyxSxd)(31d222231提示即三个变量轮换位置方程不变.Sxd22243aa具有轮换对称性,中的变量x、y、z3Sd2a对面积的曲面积分231995年研究生考题,计算,6分xyxyxz22222在柱体为锥面设.d,Sz求曲面积分内的部分解积分曲面22:yxzΣ在xOy面上的投影域xyxDxy2:2222yxz由2222yxyyzd2dS对面积的曲面积分,2222yxxxzzxyO24SzdxyD22yxd2cos2022dd232016162322cosd223339积分曲面,:22yxzd2dSxyxDxy2:22对面积的曲面积分25对面积的曲面积分的计算对面积的曲面积分的概念对面积的曲面积分四、小结四步:分割、取近似、求和、取极限思想:化为二重积分计算;对面积的曲面积分的几何意义与物理意义曲面方程三种形式的计算公式26思考题定积分、二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分可统一表示为是非题niiiΩPfPf10||||)(limd)(.,,)(PPPfii为点函数其中是对面积的曲面积分因为若Ω为直线上的区间[a,b],),()(xfPf则故.)(limd)(d)(10||||niiiΩbaPfxxfPf27思考题定积分、二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分可统一表示为是非题niiiΩPfPf10||||)(limd)(.,,)(PPPfii为点函数其中对面积的曲面积分是若Ω是平面区域G,),,()(yxfPf则故niiiiniiifPf10||||10||||),(lim)(lim.dd),(yxyxfG28思考题定积分、二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分可统一表示为是非题niiiΩPfPf10||||)(limd)(.,,)(PPPfii为点函数其中对面积的曲面积分是若Ω是空间区域,),,,()(zyxfPf则故niiiiiniiifPf10||||10||||),,(lim)(lim.ddd),,(zyxzyxf29思考题定积分、二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分可统一表示为是非题niiiΩPfPf10||||)(limd)(.,,)(PPPfii为点函数其中是若Ω为平面(空间)曲线L,),()(yxfPf则Lsyxfd),(对面积的曲面积分),),,()((zyxfPf或部分和式的极限为曲线积分).),,((),(LzyxLyx或).d),,((Lszyxf或30思考题定积分、二重积分、三重积分、对弧长的曲线积分、对面积的曲面积分可统一表示为是非题niiiΩPfPf10||||)(limd)(.,,)(PPPfii为点函数其中是若Ω为曲面Σ,则上述部分和式的极限就是.d),,(Szyxf对面积的曲面积分曲面积分31作业习题10-4(158页)3.4.(2)5.(1)6.(1)(4)7.8.对面积的曲面积分