24.4圆锥的侧面积和全面积

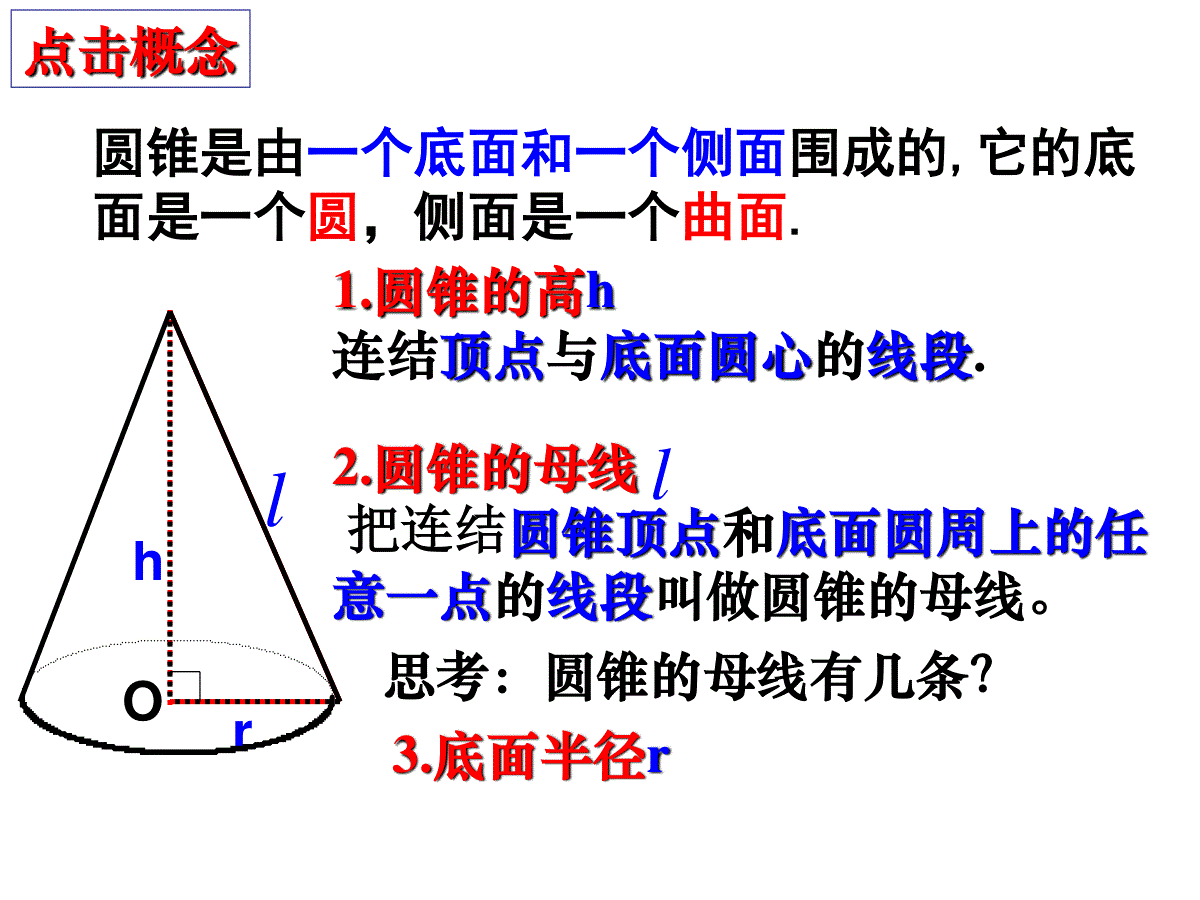
SBAO圆锥的侧面积和全面积一、圆的周长公式二、圆的面积公式C=2πrS=πr21802360rnrnl2360rnslrs21或三、弧长的计算公式四、扇形面积计算公式童心玩具厂欲生产一种圣诞老人的帽子，其帽身是圆锥形(如图)PB=15cm，底面半径r=5cm，生产这种帽身10000个，你能帮玩具厂算一算至少需多少平方米的材料吗（不计接缝用料和余料，π取3.14）？APBOrl.导入新课认识圆锥想一想圆锥知多少2.圆锥的母线把连结圆锥顶点和底面圆周上的任意一点的线段叫做圆锥的母线。1.圆锥的高h连结顶点与底面圆心的线段.点击概念圆锥是由一个底面和一个侧面围成的,它的底面是一个圆，侧面是一个曲面.思考：圆锥的母线有几条？3.底面半径rhrOll探究新知圆锥的底面半径、高线、母线长三者之间的关系:例如：已知一个圆锥的高为6cm，半径为8cm，则这个圆锥的母长为_______10cm222lhrhrOl填空、根据下列条件求值（其中r、h、a分别是圆锥的底面半径、高线、母线长）(1)a=2,r=1则h=_______(2)h=3,r=4则a=_______(3)a=10,h=8则r=_______1.圆柱的侧面展开图是一个矩形.2.圆柱的侧面积是母线与圆柱的底面圆周长围成的矩形面积.3.圆柱的全面积=侧面积+底面积回顾圆柱的侧面积母线底面圆周长1．准备好的圆锥模型沿着母线剪开，观察圆锥的侧面展开图．图23.3.6图23.3.7动动手问题1:1.沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形，这个扇形的弧长与底面的周长有什么关系？图23.3.7探究新知相等母线2.圆锥侧面展开图是扇形，这个扇形的半径与圆锥中的哪一条线段相等？问题2：图23.3.6如图23.3.7，沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形。扇形的弧长=圆锥底面的周长扇形的半径=圆锥的母线的长．圆锥的侧面展开图是一个扇形.２．探究a2лr圆锥的侧面积和全面积如图:设圆锥的母线长为L,底面半径为r.则圆锥的侧面积公式为：全面积公式为：SSS底侧全+==πrl＋πr2rLπ2=OPABrhlraralaS22121侧例1、根据圆锥的下列条件,求它的侧面积和全面积.(1)r=12cm,a=20cm;(2)h=12cm,r=5cm.×24π×2012=240π圆锥侧面积:圆锥全面积:240π+144π=384π×10π×1312=65π圆锥侧面积:圆锥全面积:65π+25π=90π1.填空（1）已知圆锥的底面直径为4，母线长为6，则它的侧面积为_________.12π6πcm210πcm2（2）已知圆锥底面圆的半径为2cm，高为，则这个圆锥的侧面积为_________；全面积为_________．cm525童心玩具厂欲生产一种圣诞老人的帽子，其圆锥形帽身的母线长为15cm，底面半径为5cm，生产这种帽身10000个，你能帮玩具厂算一算至少需多少平方米的材料吗（不计接缝用料和余料，π取3.14）？解:∵a=15cm,r=5cm,235.5×10000=2355000(cm2)答：至少需235.5平方米的材料.∴S侧=πra3.14×15×5=235.5(cm2)ra例2蒙古包可以近似地看成有圆锥和圆柱组成.如果想用毛毡塔建20个底面积为12m2，高为3.2m，外围高为1.8m的蒙古包，至少需要多少平方米的毛毡？（π取3.142，结果取整数）rrh1h2解：如图，是一个蒙古包示意图.根据题意，得：1h下部圆柱的底面积为12m2，高为1.8m；上部圆锥的高==（m)1hSr2∵即：r=S∴圆柱的底面半径为r=≈1.954m.∴圆锥的母线长==_________≈2.404（m)，圆锥侧面积展开扇形的弧长为2π×≈（m)∴圆锥侧S=≈（m2)∴搭建20个这样的蒙古包至少需要毛毡20×（+)≈（m2).8.12.34.1128.1954.12224.1954.1954.128.1228.12404.22176.1210.2228.12738=≈22.10（m2)rrh1h2你会计算展开图中的圆心角的度数吗？lrha180anl1801802rr360alnaanrl2又aln180rha例2、根据下列条件求圆锥侧面积展开图的圆心角（r、h、a分别是圆锥的底面半径、高线、母线长）(1)a=2，r=1(2)h=3,r=43.若圆锥的底面半径r=4cm，高线h=3cm，则它的侧面展开图中扇形的圆心角是——度。4.如图，若圆锥的侧面展开图是半圆，那么这个展开图的圆心角是___度；圆锥底半径r与母线a的比r：a=___.2881801:2lrhSBAO2.如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120度,则该圆锥的侧面积为_____,全面积为_______300π400π例2.如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少?ABC61B’解:设圆锥的侧面展开图为扇形ABB’,∠BAB’=n°∴△ABB’是等边三角形答:蚂蚁爬行的最短路线为6.解得:n=60∵圆锥底面半径为1,连接BB’,即为蚂蚁爬行的最短路线又∵l弧BB’=6nπ180∴2π=∴BB’=AB=66nπ180例3、如图，圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上，问它爬行的最短路线是多少？.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′.323323.3,60.60120360.它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′.323323.3,60.60120360.它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′ABC.323323∴.3,60∠Δ.60∠∴120360∠.⊥它爬行的最短路线是答中在垂足为作过点的中点是则点展开成扇形将圆锥沿解：BDABBAD，ABCRtBADlrBBADAC，BDB，BBC，BABAB：==°=°=°=°×=′′′将圆锥沿AB展开成扇形ABB’3nπ1802π=再见