当前位置:首页 > 建筑/环境 > 工程监理 > 第07讲简单体系――势垒贯穿1
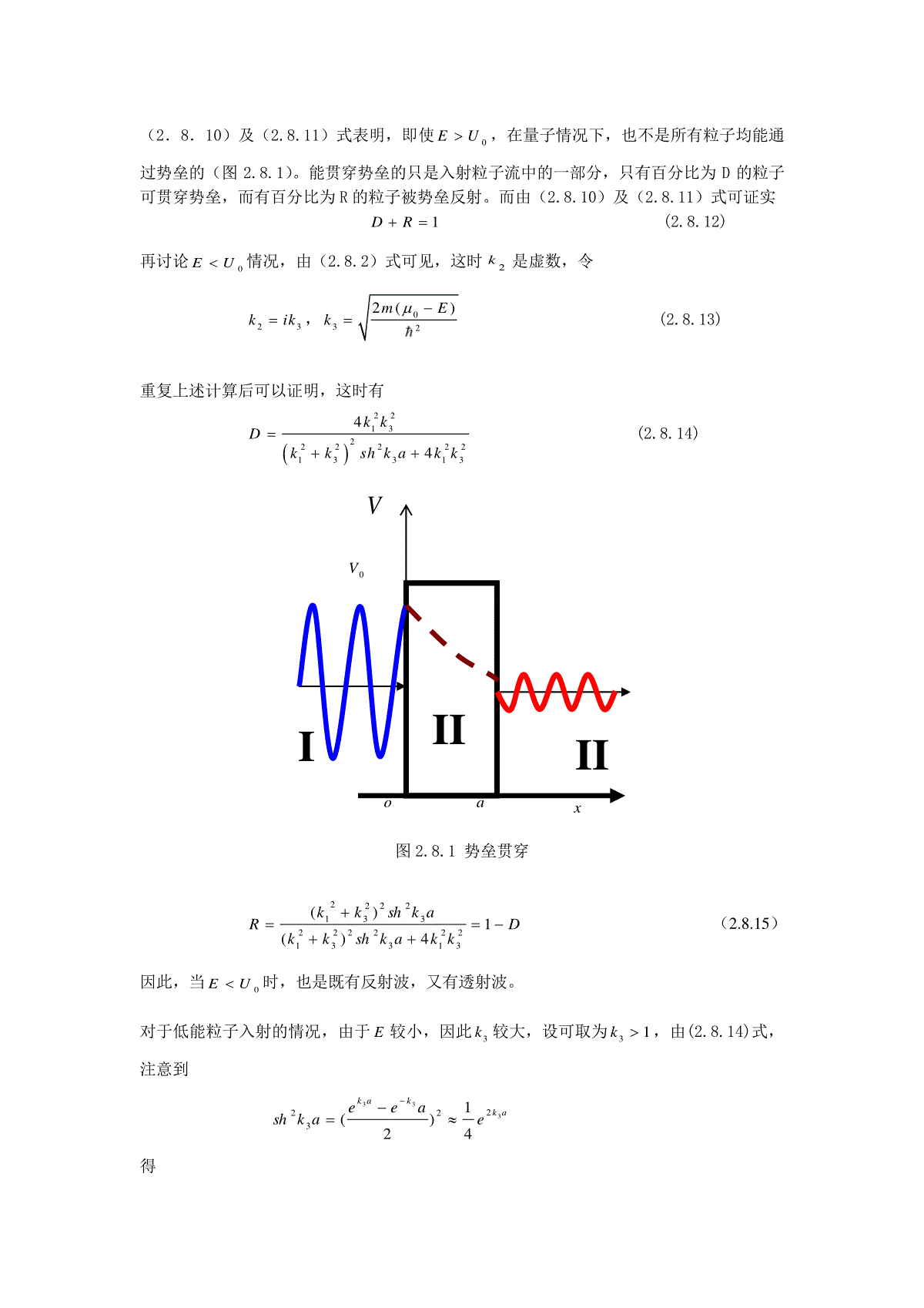
第07讲简单体系――势垒贯穿前面讨论了束缚态.现在开始讨论散射态。首先讨论一维空间中势垒贯穿问题.以方势垒为;例,设势场为0(0)()0(0,)XaUUxxxa(2.8.1)(2.8.1)式中,00U.正在经典力学中,若粒子能量EU。,则粒子可能越过势场,不受势场影响,完全透射。若粒子能量EU。,则粒子完全不可能越过势场,被全部反射.但量子力学的情况却完全不同,我们将证明,无论0EU还是0UE,反射和透射波都会同时存在。先讨论0EU情况。相应于各区的薛定谔方程是),0(2,0212122axxmEdkkxd,02222kxdd)0()(2202axEmUk(2.8.2)在各个不同区域的解是eAexixikkA11'1(x0)eBexixikkB22'2(0xa)(2.8.3)exikC13(xa)其中11xikAe是在x0区中的入射波和反射波和反射波,xkBei2和xkeBi'2是在ax0区中的右行的左行的波,xkCei1是在ax区的透射波。由于在ax区中无反射,因此不出现xkeCi1'项。利用在0x和ax处波函数连续和波函数微商连续条件,得''BBAA1122''kAkAkBkB221'ikaikaikaBeBeCe(2.8.4)221221'ikaikaikakBekBeCke(2.8.4)式中有四个方程式,但有五个未知数''AABBC、、、、,因此利用简单的代数运算,总可将''ABBC、、、表示为A的函数,于是得122122212124ikaikaikakkeCAkkekke(2.8.5)22221222212122()sin'ikaikaikkkaAAkkekke(2.8.6)利用概率流公式(2.3.17)式,可算出相应于入射波1ikinAex的入射概率流密度Jin为Jin=*2*1()2kiddmdxdxmA(2.8.7)相应于透射波exiDkC1的透射概率流密度JD是JD=21kmC(2.8.8)相应于反射波1'ikxRAe的反射概率流密度是AkJmR'21(2.8.9)定义透射系数或称贯穿系数为222122222222122124sin4DinCJkkDJAkkkakk(2.8.10)反射系数为2222122222222212212sin'sin4RinkkkaAJRJAkkkakk(2.8.11)(2.8.10)及(2.8.11)式表明,即使0EU,在量子情况下,也不是所有粒子均能通过势垒的(图2.8.1)。能贯穿势垒的只是入射粒子流中的一部分,只有百分比为D的粒子可贯穿势垒,而有百分比为R的粒子被势垒反射。而由(2.8.10)及(2.8.11)式可证实1DR(2.8.12)再讨论0UE情况,由(2.8.2)式可见,这时2k是虚数,令23kik,0322()mEk(2.8.13)重复上述计算后可以证明,这时有22132222221331344kkDkkshkakk(2.8.14)图2.8.1势垒贯穿DkkakshkkakshkkR14)()(232132223213222321(2.8.15)因此,当0UE时,也是既有反射波,又有透射波。对于低能粒子入射的情况,由于E较小,因此3k较大,设可取为31k,由(2.8.14)式,注意到akkakeaeeaksh333223241)2(得0VVaoxIIIIIIadxEUmhaEUmhakeeeD0003)(22)(222(2.8.16)势垒越高,U。越大,D越小;势垒越宽,a越大,D也越小,因此势垒越高,越宽,越难穿透,若0U,3k,0D,在非相对论量子力学中,粒子不可能穿透无限高的势垒。对于透射波,由于D在x时不为零,它的归一化要另外讨论。如果我们讨论的不是方势垒,而是方势阱,则显然,只是将上面的结果作代换u0-u0,即将2022)(2UEmkk(2.8.17)仍然可由(2.8.10)式给出方势阱的透射系数。现在讨论在何种情况下D=1,粒子完全透射。显然,若u0=0,22kk,R=0,D=1,但这只是个平庸的情况,相当于粒子完全不受势场散射。除此之外,若nak2(n=1,2…)(2.8.18)D也等于1。这时的透射称为共振透射,相应的共振能量022222UmanE(2.8.19)问题1若定义共振宽度为D从1降到1/2时,所对应共振能级的宽度为E,试证明当能量E增加时,E增加问题2设粒子连续穿过两个高度均为u0,宽度均为a的方势垒,求透射系数。例1求势垒的贯穿系数。解:对势垒,势场为xUxU()0U(2.8.20)薛定谔方程是02222UEdxdm(2.8.21)对上述方程两边作积分dx0lim,得)0()0()0(20''2Um(2.8.22)令'(0)()(0)ikxikxikxeAexxCex,22,mEk(2.8.23)代入(2.8.22)式得CUACmik0'2)1(2(2.8.24)由在x=0处的连续条件又可得1+Aˊ=C(2.8.25)联立(2.8.24)式和(2.8.25)式,消去Aˊ,得CkimU211(2.8.26)透射系数是D=c2=1242211khUm=22211EhmU(2.8.27)



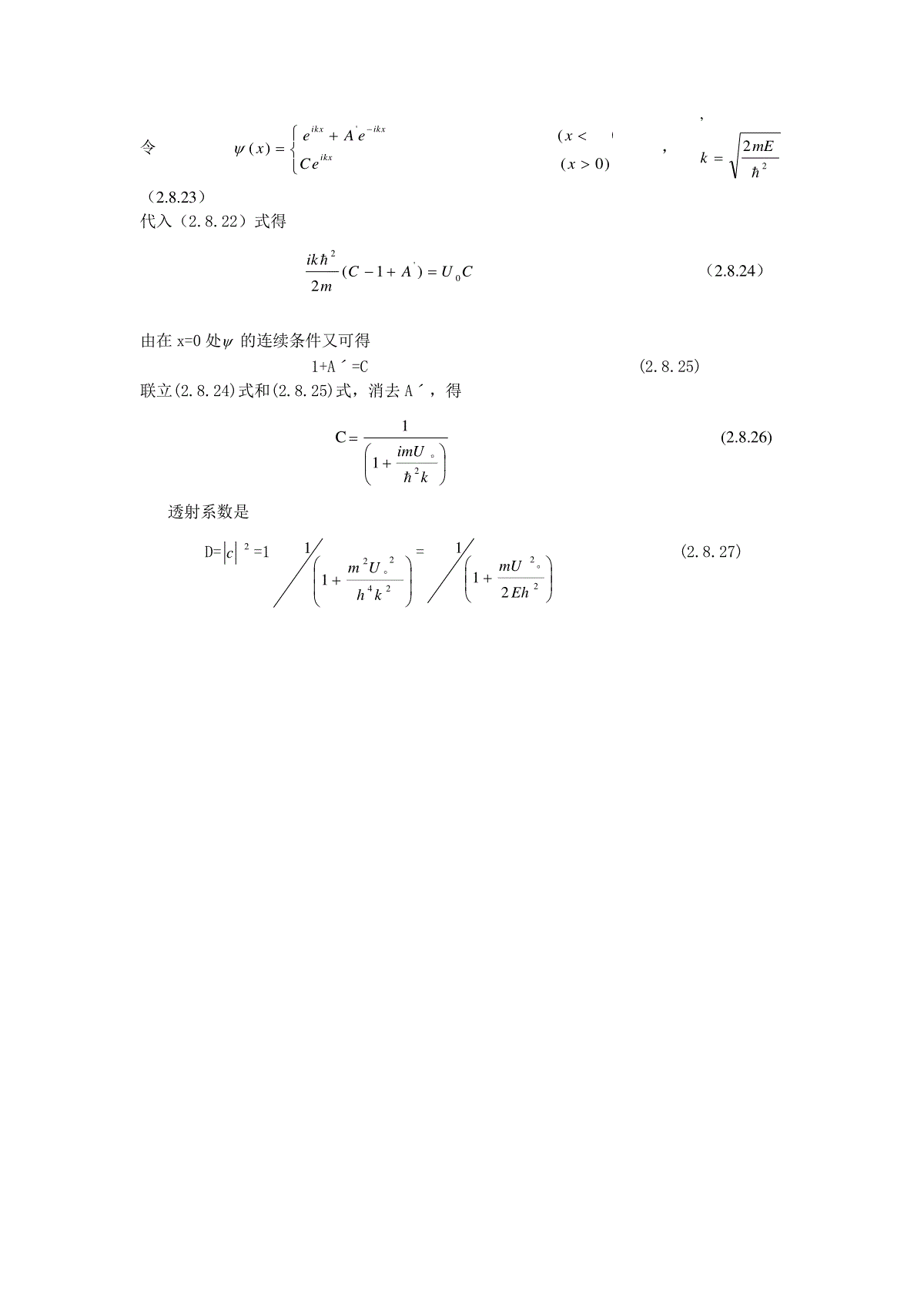
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:第07讲简单体系――势垒贯穿1
链接地址:https://www.777doc.com/doc-2241295 .html