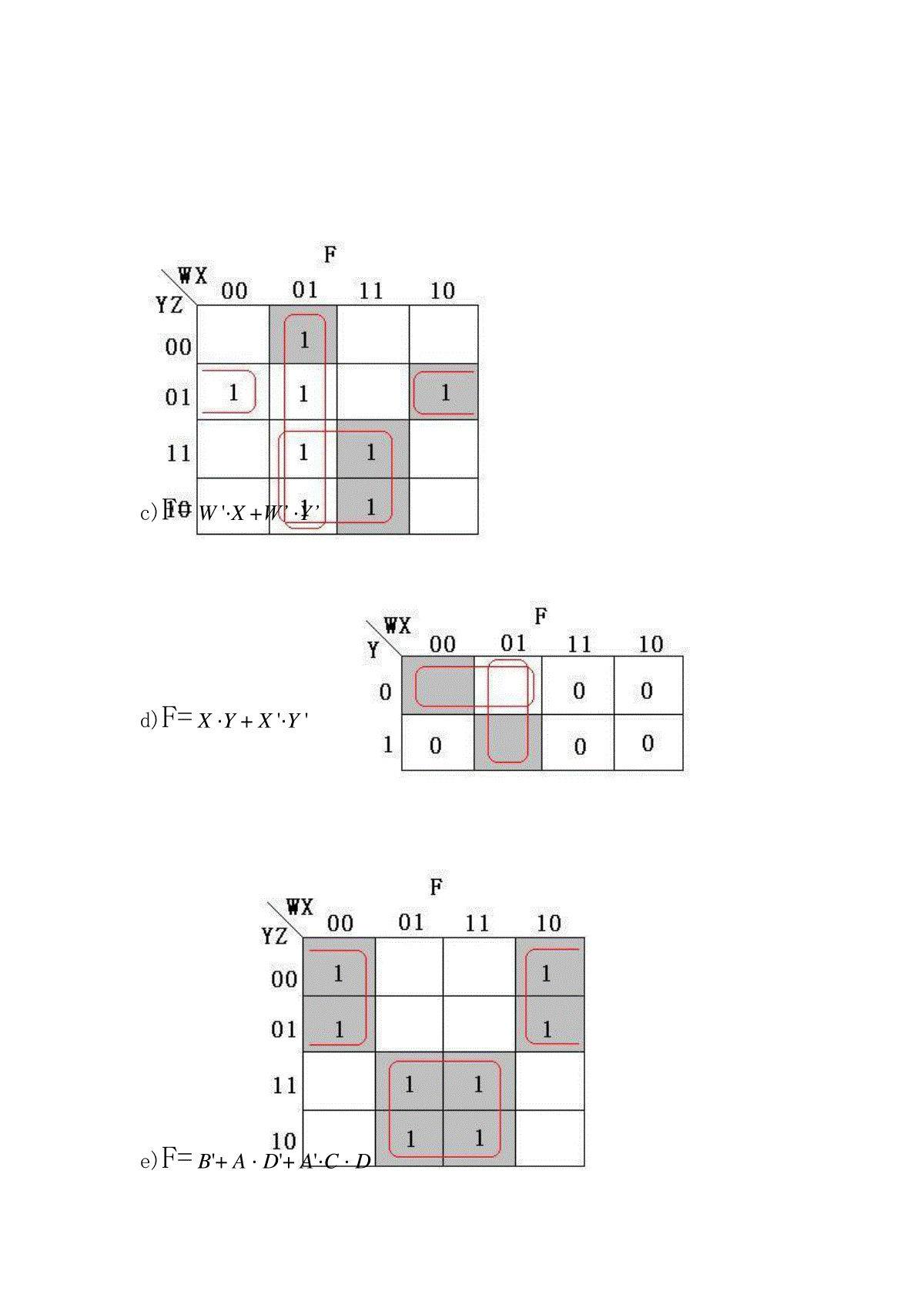
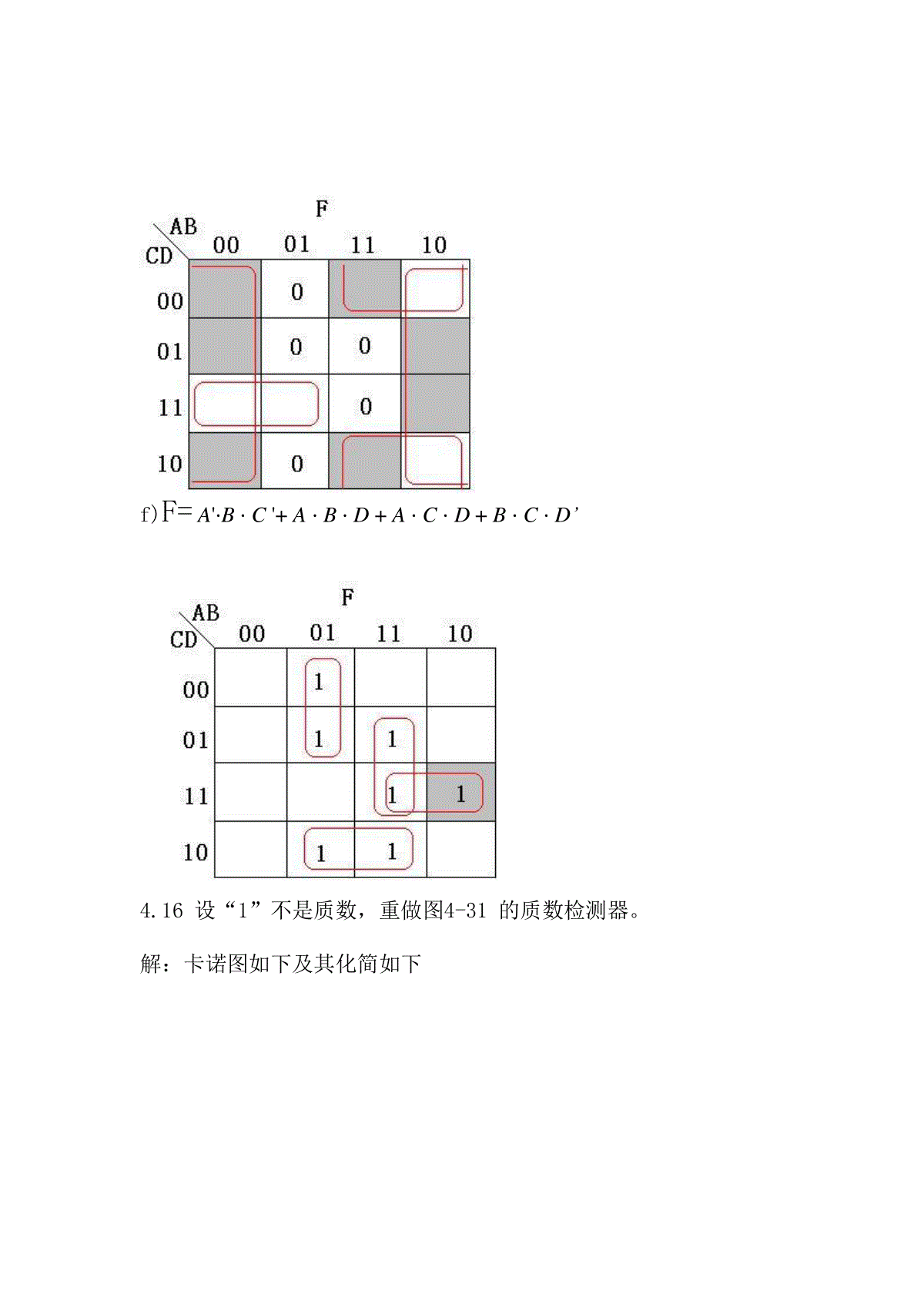
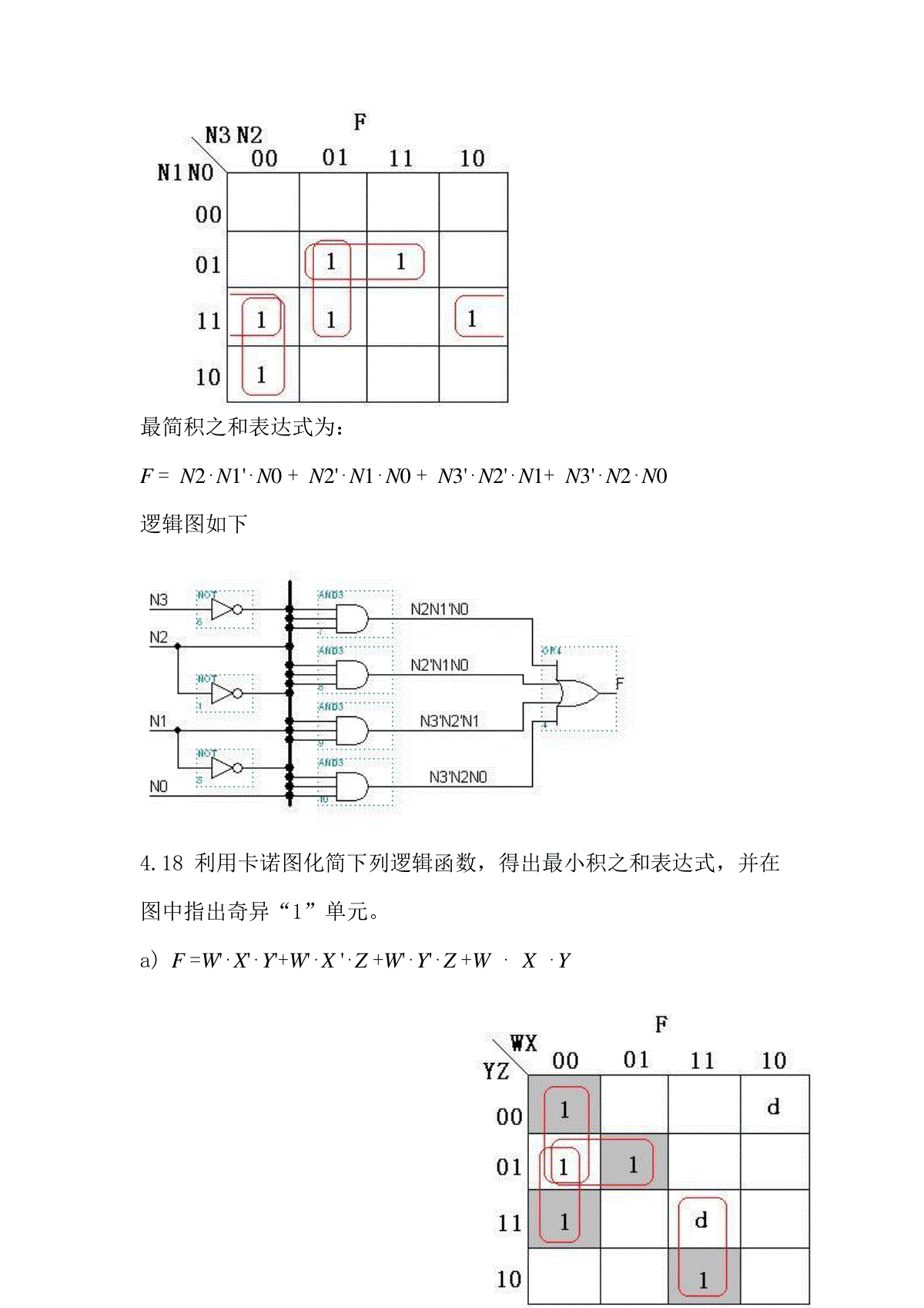
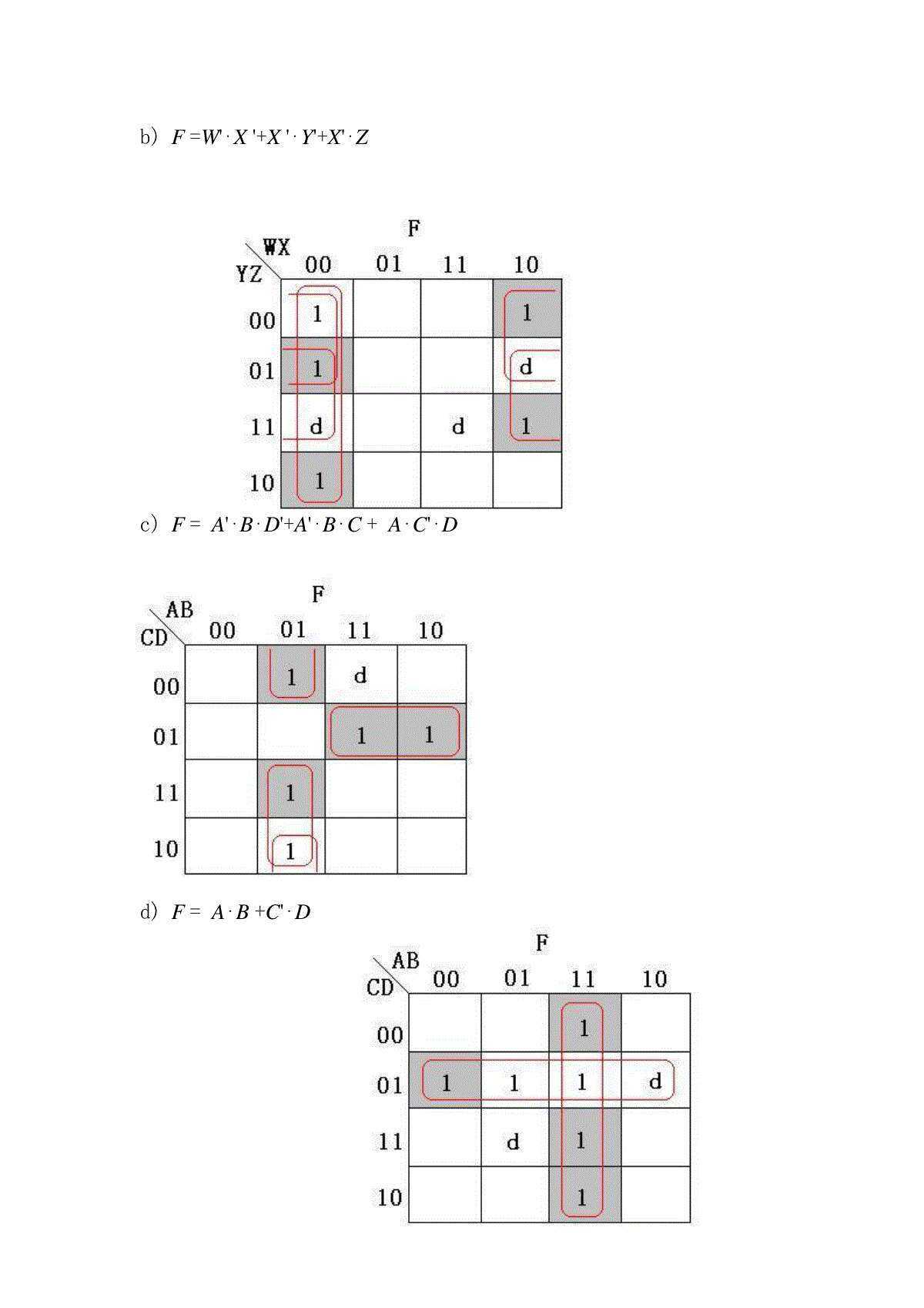
4.5答:在利用定理时,没有考虑到运算先后顺序,“⋅”的优先级高于“+”,正确的补函数应该为:(W⋅X+Y⋅Z)'=(W⋅X)'⋅(Y⋅Z)'=(W'+X')(Y'+Z')当WXYZ=1110时,W⋅X+Y⋅Z=1,(W⋅X+Y⋅Z)'=(W⋅X)'⋅(Y⋅Z)'=04.6(a)F=W⋅X⋅Y⋅Z(W⋅X⋅Y⋅Z′+W⋅X′⋅Y⋅Z+X⋅Y⋅Z⋅W′+W⋅X⋅Y′⋅Z)=W⋅X⋅Y⋅Z⋅W⋅X⋅Y⋅Z′+W⋅X⋅Y⋅Z⋅W⋅X′⋅Y⋅Z+W⋅X⋅Y⋅Z⋅W′⋅X⋅Y⋅Z+W⋅X⋅Y⋅Z⋅W⋅X⋅Y′⋅Z=0(b)F=A⋅B+A′⋅C′⋅E(c)F=M⋅R⋅P+M⋅N+Q⋅O′⋅R′+Q⋅P⋅M⋅O′4.9请写出下面各个逻辑函数的标准和与标准积.a)F=ΣX,Y(1,2)=ΠX,Y(0,3)标准和:F=X⋅Y'+X'⋅Y标准积:F=(X+Y)⋅(X'+Y')b)F=ΠA,B(0,1,2)=ΣA,B(3)标准和:F=A⋅B标准积:F=(A+B)⋅(A+B')⋅(A'+B)c)F=ΣA,B,C(1,2,4,6)=ΠA,B,C(0,3,5,7)标准和:F=A'⋅B'⋅C+A'⋅B⋅C'+A⋅B'⋅C'+A⋅B⋅C'标准积:F=(A+B+C)⋅(A+B'+C')⋅(A'+B+C')⋅(A'+B'+C')d)F=ΠW,X,Y(0,2,3,6,7)=ΣW,X,Y(1,4,5)标准和:F=W'⋅X'⋅Y+W⋅X'⋅Y'+W⋅X'⋅Y标准积:F=(W+X+Y)⋅(W+X'+Y)⋅(W+X'+Y')⋅(W'+X'+Y)⋅(W'+X'+Y')e)F=X'+Y⋅Z=ΣX,Y,Z(0,1,2,3,7)=ΠX,Y,Z(4,5,6)标准和:F=X'⋅Y'⋅Z'+X'⋅Y'⋅Z+X'⋅Y⋅Z'+X'⋅Y⋅Z+X⋅Y⋅Z标准积:F=(X'+Y+Z)⋅(X'+Y+Z')⋅(X'+Y'+Z)f)F=V+(W⋅X')'=ΠV,W,X(2)=ΣV,W,X(0,1,3,4,5,6,7)标准和:F=V'⋅W'⋅X'+V'⋅W'⋅X+V'⋅W⋅X+V⋅W'⋅X'+V⋅W'⋅X+V⋅W⋅X'+V⋅W⋅X标准积:F=V+W'+X4.14利用卡诺图化简下列逻辑函数,得出最小积之和表达式,并在图中指出奇异“1”单元。a)F=ΣX,Y,Z(1,3,5,6,7)=Z+XYb)F=W'⋅X+X⋅Y+X'⋅Y'⋅Zc)F=W'⋅X+W’⋅Y’d)F=X⋅Y+X'⋅Y'e)F=B'+A⋅D'+A'⋅C⋅Df)F=A'⋅B⋅C'+A⋅B⋅D+A⋅C⋅D+B⋅C⋅D’4.16设“1”不是质数,重做图4-31的质数检测器。解:卡诺图如下及其化简如下最简积之和表达式为:F=N2⋅N1'⋅N0+N2'⋅N1⋅N0+N3'⋅N2'⋅N1+N3'⋅N2⋅N0逻辑图如下4.18利用卡诺图化简下列逻辑函数,得出最小积之和表达式,并在图中指出奇异“1”单元。a)F=W'⋅X'⋅Y'+W'⋅X'⋅Z+W'⋅Y'⋅Z+W⋅X⋅Yb)F=W'⋅X'+X'⋅Y'+X'⋅Zc)F=A'⋅B⋅D'+A'⋅B⋅C+A⋅C'⋅Dd)F=A⋅B+C'⋅De)F=X⋅Y'+W⋅Z4.19对下列逻辑表达式,找出对应2级AND-OR或OR-AND的所有静态冒险。设计无冒险的电路实现同样的逻辑。解:先利用表达式写出对应的卡诺图(保存各项对应的圈),找出静态冒险发生的变量组合条件,再针对这些条件进行设计。a)F=W⋅X+W'⋅Y'静态1冒险:X⋅Y'=1无冒险设计:F=W⋅X+W'⋅Y'+X⋅Y'c)F=W⋅Y+W'⋅Z'+X⋅Y'⋅Z静态1冒险:W'⋅X⋅Y'=1W⋅X⋅Z=1X⋅Y⋅Z'=1X'⋅Y⋅Z'=1无冒险设计:F=W⋅Y+W'⋅Z'+X⋅Y'Z+W'⋅X⋅Y'+W⋅X⋅Z+Y⋅Z'e)F=(W'+X+Y')⋅(X'+Z')静态0冒险:W'+Y'+Z'=0无冒险设计:F=(W'+X+Y')⋅(X'+Z')⋅(W'+Y'+Z')g)F=(W+Y+Z')⋅(W+X'+Y+Z)⋅(X'+Y')⋅(X+Z)静态0冒险:W+Y+Z=0W+Y'+Z=0W'+Y'+Z=0W+X'+Z=0W+X'+Z'=0W+Y=0无冒险设计:F=(W+Y)⋅(W+X')⋅(Y'+Z)⋅(X'+Y')⋅(X+Z)4.25解:根据逻辑定理:(x1+x2+x3+x4+x5+...)=((((x1+x2)+x3)+x4)+x5)+...第1次运算实现2个变量的OR,第2次运算实现3个变量的OR,第(n-1)次运算就可以实现n个变量的OR。NOR不能这样做以3个变量为例:利用DeMorgan’s定理((x1+x2)’+x3)’=(x1’+x2’+x3)’≠(x1+x2+x3)’所以不能采用这种方式替换4.36真值表逻辑式:逻辑图:4.38答:只能利用XNOR实现,在逻辑表达式F=A⋅B+A’⋅B’中,令B或A等于0(将该输入端接地),即可实现反相器功能。4.58解:先将所给函数填入卡诺图,再利用卡诺图进行化简(a)F=X'⋅Z+X⋅Y+X⋅Y'⋅ZF=Z+X⋅Y(b)F=A'⋅C'⋅D+B'⋅C⋅D+A⋅C'⋅D+B⋅C⋅DF=D(c)F=W'⋅X+W⋅X⋅Y⋅Z+W'⋅ZF=W'⋅X+X⋅Y⋅Z+W'⋅Z(d)F=(W+Z')(W'+Y'+Z')(X+Y'+Z)F=Y'⋅Z'+X⋅Z'+W⋅Y'(e)F=A'⋅B'⋅C'⋅D'+A'⋅C'⋅D+B⋅C'⋅D'+A⋅B⋅D+A⋅B'⋅C'F=C'+A⋅B⋅D4.56F=X'⋅Y'⋅Z+X⋅ZG=X'⋅Y'⋅Z+X⋅ZH=X'⋅Y'⋅Z+X'⋅Z'+X⋅Z

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:数字逻辑设计第四章
链接地址:https://www.777doc.com/doc-2425709 .html