2013年排列组合概率单元考试试题

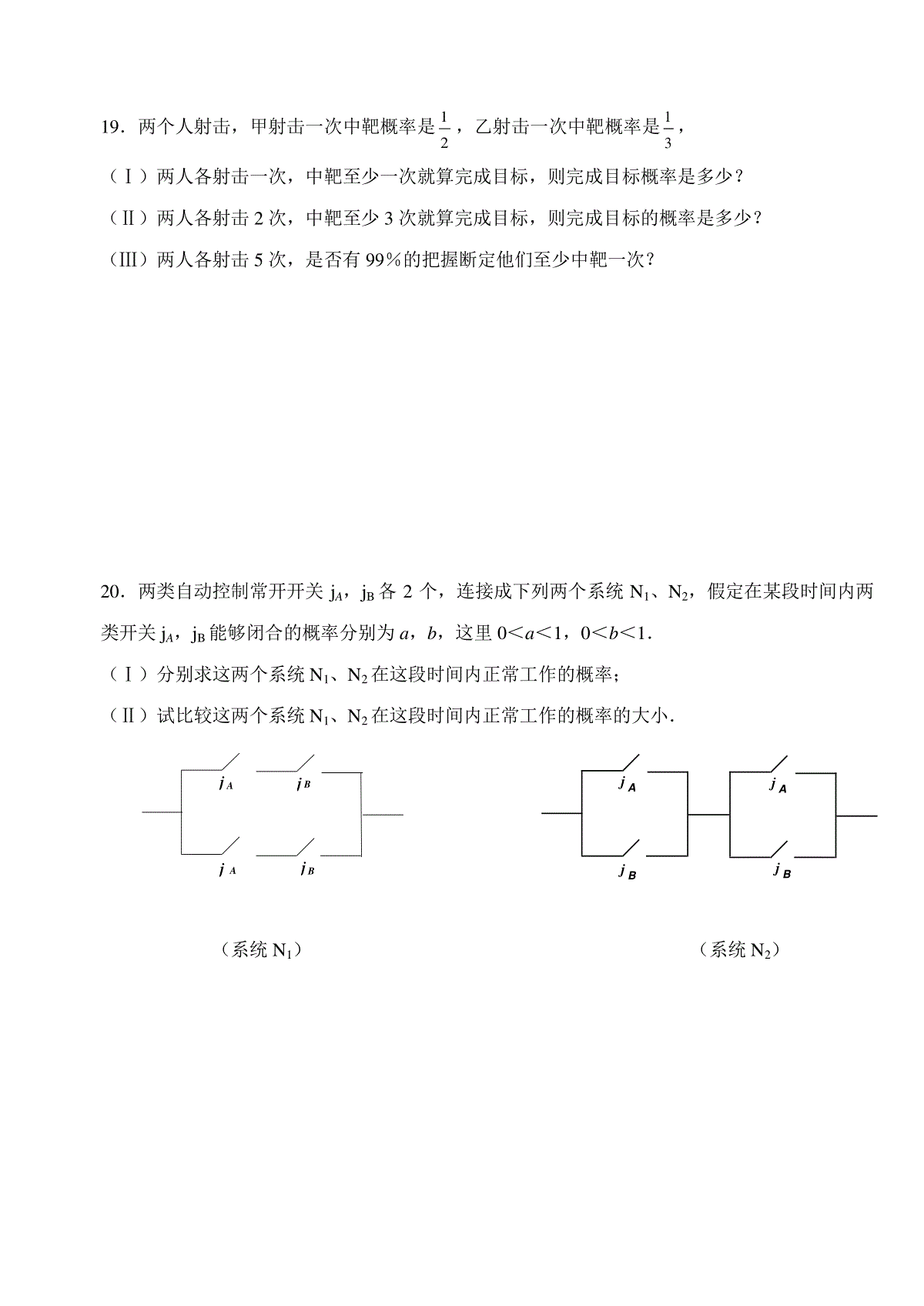
新邵四中高二数学单元考试《排列组合、二项式定理》与《概率》班级_________________姓名____________________一．选择题1．某办公室有8人，现从中选出3人参加A，B，C三项活动，其中甲不得参加A项活动，则不同的选派方法有（）A．35种B．56种C．294种D．336种2．A，B，C，D，E五种不同商品要在货架上排成一排，其中A，B两种商品必须排在一起，而C，D两种商品不能排在一起，则不同的排法共有（）A．12种B．20种C．24种D．48种3．在三张卡片的正反面上分别写有数字0与2，3与4，5与6，且6可以作9用，把这三张卡片拼在一起表示一个三位数，则三位数的个数为（）A．12B．72C．60D．404．若nxx)1(23的展开式中只有第6项的系数最大，则常数项的值为（）A．462B．252C．210D．105．1.056的计算结果精确到0.01的近似值是（）A．1.23B．1.24C．1.34D．1.446．两个同学同时做一道题，他们做对的概率分别为P(A)=0.8,P(B)=0.9，则该题至少被一个同学做对得概率为（）A．1.7B．1C．0.72D．0.987．一个学生通过一种英语听力测试的概率是21，他连续测试两次，那么其中恰有一次通过的概率是（）A.41B.31C.21D.438．已知在6个电子元件中，有2个次品，4个合格品，每次任取一个测试，测试完后不再放回，直到两个次品都找到为止，则经过4次测试恰好将2个次品全部找出的概率（）A.51B.154C.52D.15149．n个人随机进入n个房间，每个人可以进入任何一个房间，且进入各房间是等可能的，则每个房间恰好进入一个人的概率为（）A．n1B．nnn!C．)!1(1nD．nnn)!1(10．某校高二年级举行的一次演讲比赛共有10位同学参赛，其中一班有3位，二班有2位，其他班有5位，若采取抽签的方式确定他们的演讲顺序，则一班的3位同学恰好被排在一起(指演54321讲序号相连)，而二班的2位同学没有被排在一起的概率为()A．101B．201C．401D．1201二．填空题11．6)2||1|(|xx展开式中系数最大的项的系数为_________．12．设二项式nxx)13(3展开式的各项系数的和为P；二项式系数的和为S，且P+S=272，则展开式的常数项为_________．13．如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有种奎屯王新敞新疆14．5个正四面体小木块表面上，分别标有1，2，3，4，如果把这5块小木块全部掷出，则至多有1块小木块标有4的面因贴在桌面上而看不见的概率是.15．将正整数n表示成k个正整数的和（不计较各数的次序），称为将正整数n分成k个部分的一个划分，一个划分中的各加数与另一个划分的各加数不全相同，则称为不同的划分，将正整数n划分成k个部分的不同划分的个数记为P（n，k），则P（10，3）＝______________．三．解答题16．用数字0，1，2，3，4，5组成没有重复数字的数，（1）能组成多少个是25的倍数的四位数；（2）能组成多少个比240135大的数；（3）若把所组成的全部六位数从小到大排列起来，第100个数是多少？17．（甲、乙两题中任选一题）（甲）在二项式nx)221(的展开式中，（1）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；（2）若前三项的二项式系数和等于79，求展开式中系数最大的项．（乙）设m，n∈Z+，m、n≥1，f（x）=（1+x）m+（1+x）n的展开式中，x的系数为19奎屯王新敞新疆（1）求f（x）展开式中x2的系数的最大值、最小值；（2）对于使f（x）中x2的系数取最小值时的m、n的值，求x7的系数奎屯王新敞新疆18．有6个房间安排4个旅游者住宿，每人可以随意进哪一间，而且一个房间也可以住几个人奎屯王新敞新疆求下列事件的概率：（1）事件A：指定的4个房间中各有1人；（2）事件B：恰有4个房间中各有1人；（3）事件C：指定的某个房间中有两人；（4）事件D：第1号房间有1人，第2号房间有3人奎屯王新敞新疆19．两个人射击，甲射击一次中靶概率是21，乙射击一次中靶概率是31，（Ⅰ）两人各射击一次，中靶至少一次就算完成目标，则完成目标概率是多少？（Ⅱ）两人各射击2次，中靶至少3次就算完成目标，则完成目标的概率是多少？（Ⅲ）两人各射击5次，是否有99％的把握断定他们至少中靶一次？20．两类自动控制常开开关jA，jB各2个，连接成下列两个系统N1、N2，假定在某段时间内两类开关jA，jB能够闭合的概率分别为a，b，这里0＜a＜1，0＜b＜1．（Ⅰ）分别求这两个系统N1、N2在这段时间内正常工作的概率；（Ⅱ）试比较这两个系统N1、N2在这段时间内正常工作的概率的大小．（系统N1）（系统N2）jAjBjAjBjAjBjAjB参考答案：一．选择题(每题3分)1．C．294271237ACA；2．C．24232222AAA；3．C．6033131222121312ACCACCC；4．C．5．C．6．D．7．C．8．B．15414613CC；9．B．10．B二．填空题（每题4分）11．612C；12．108．n=4；13、72；14．12881)41()43()43(445555CC；15．8；三．解答题(每题10分)16．（1）21241313ACC；（2）4071234455AA；（3）150342.17．（甲）（1）5642nnnCCC∴n=7或n=14，当n＝7时，展开式中二项式系数最大的项是T4和T5，且44347533437470)2()21(,235)2()21(xxCTxxCT；当n＝14时，展开式中二项式系数最大的项是T8,，且77771483432)2()21(xxCT；（2）79210nnnCCC∴n=12设Tk+1项系数最大，121212)41()21()221(xx∴1112121112124444kkkkkkkkCCCC∴9.4k10.4∴k=10（乙）解：19,1911nmCCnm即奎屯王新敞新疆nm19（1）设x2的系数为T=22nmCC419171)219(17119222nnn奎屯王新敞新疆∵n∈Z+，n≥1，∴当,153,181maxTnn时或当81,109minTn时或奎屯王新敞新疆（2）对于使f（x）中x2的系数取最小值时的m、n的值，即109)1()1()(xxxf从而x7的系数为15671079CC奎屯王新敞新疆18.解：4个人住进6个房间，所有可能的住房结果总数为：（种）（1）指定的4个房间每间1人共有44A种不同住法奎屯王新敞新疆54/16/)(444AAP奎屯王新敞新疆（2）恰有4个房间每间1人共有46A种不同住法奎屯王新敞新疆18/56/)(446ABP（3）指定的某个房间两个人的不同的住法总数为：5524C（种），216/256/5)(4224CCP奎屯王新敞新疆（4）第一号房间1人，第二号房间3人的不同住法总数为：43314CC（种），324/16/4)(4D奎屯王新敞新疆19．（Ⅰ）共三种情况：乙中靶甲不中313221；甲中靶乙不中613121；甲乙全613121。∴概率是32316161。（Ⅱ）两类情况:共击中3次61)31()31()21()21()32()31()21()21(0222111211120222CCCC；共击中4次361)32()31()21()21(02220222CC，36736161概率为．（III）0505551212421()()10.9923243243CC，能断定.20．（Ⅰ）系统N1正常工作的概率为P(N1)=1－(1－ab)2=2ab－a2b2；系统N2正常工作的概率为：P(N2)=[1－(1－a)(1－b)]2=a2+b2+a2b2－2a2b－2ab2+2ab；（Ⅱ）∵P(N2)－P(N1)=(a2+b2+a2b2－2a2b－2ab2+2ab)－(2ab－a2b2)=a2+b2－2a2b－2ab2+2a2b2=a2(b-1)2+b2(a-1)20，(或者≥2ab－2a2b－2ab2+2a2b2=2ab(1－a)(1－b)0)∴在这段时间内系统N2正常工作的概率大于系统N1的概率。