2004年苏州市数学中考试题及答案

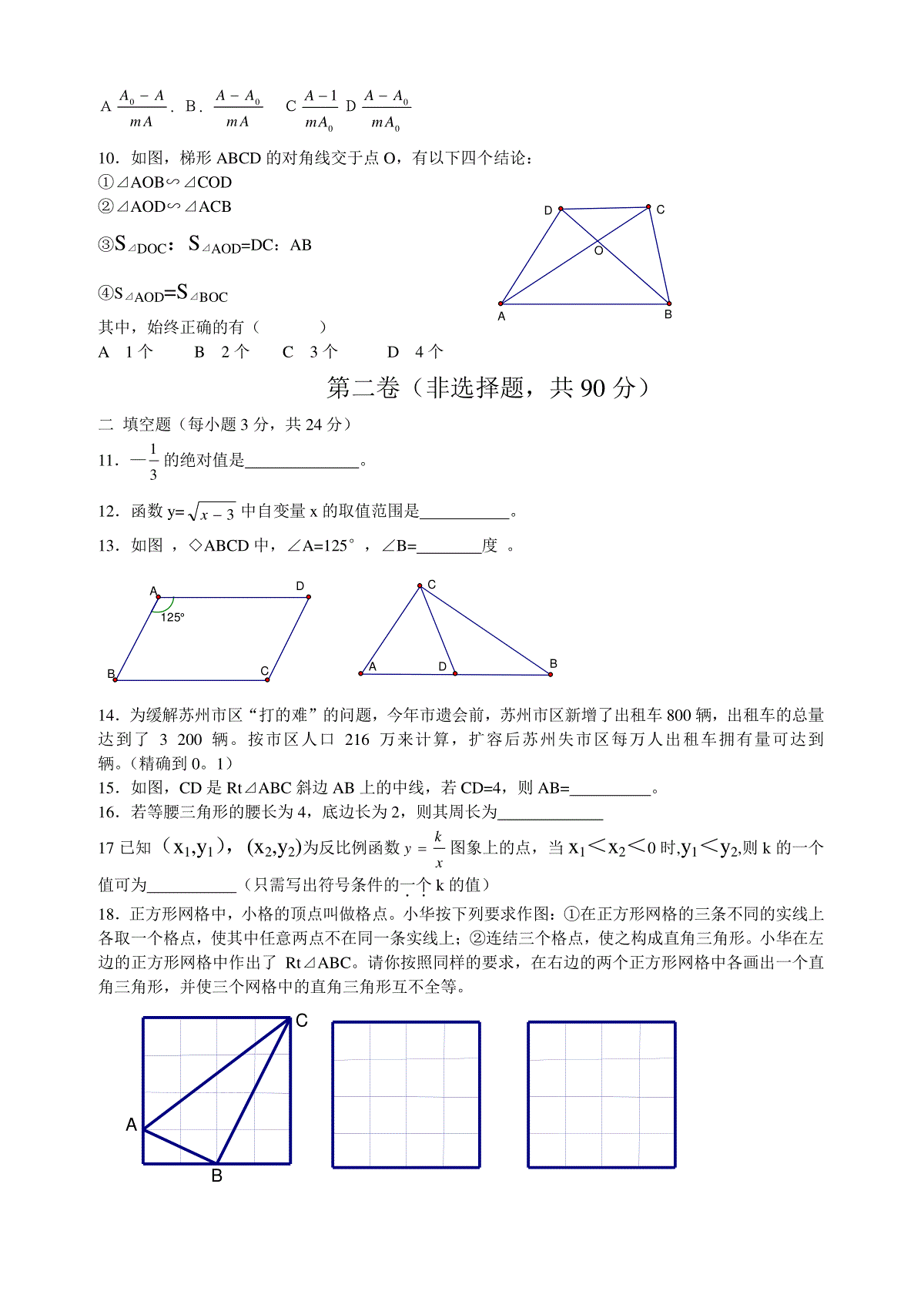
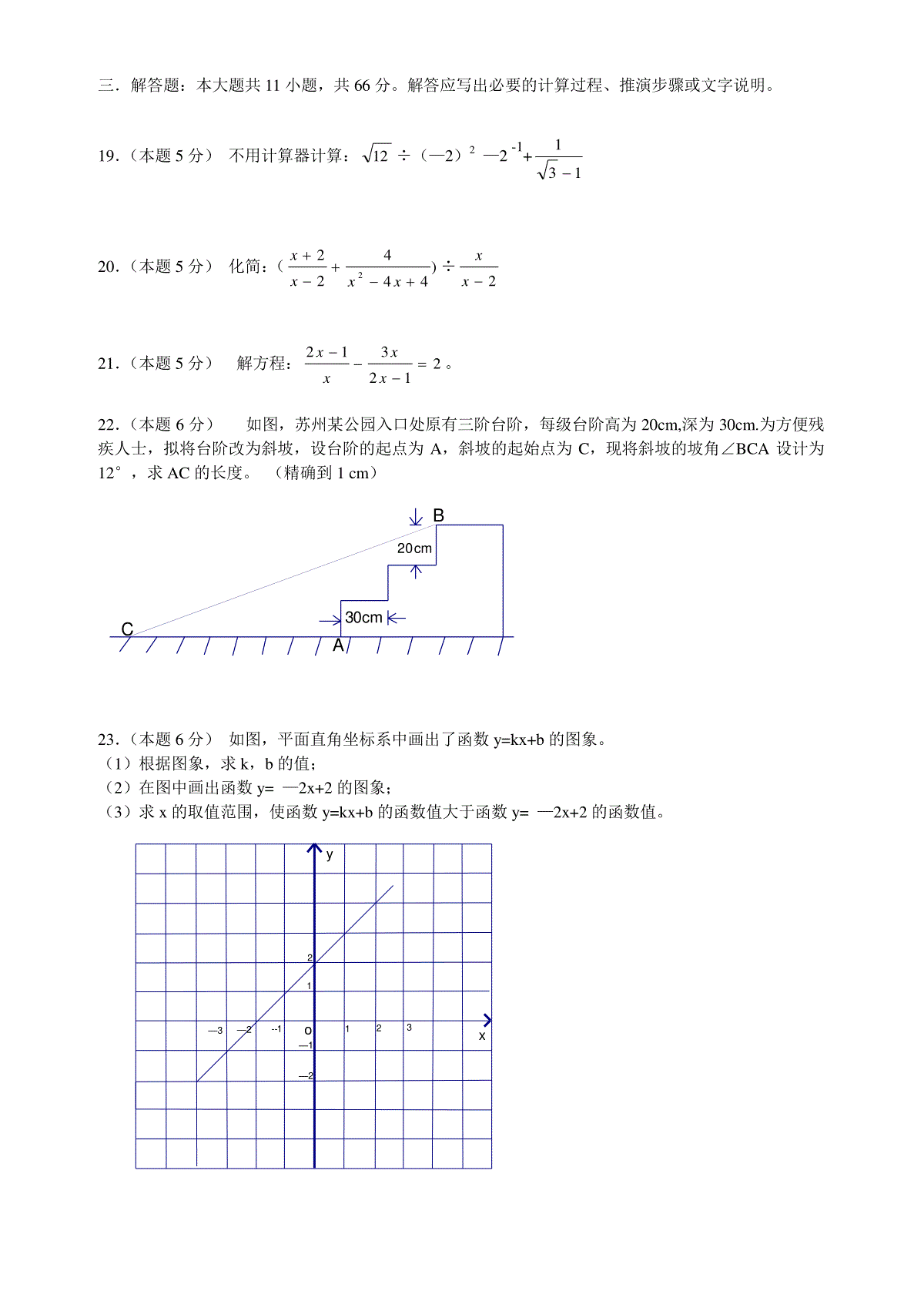
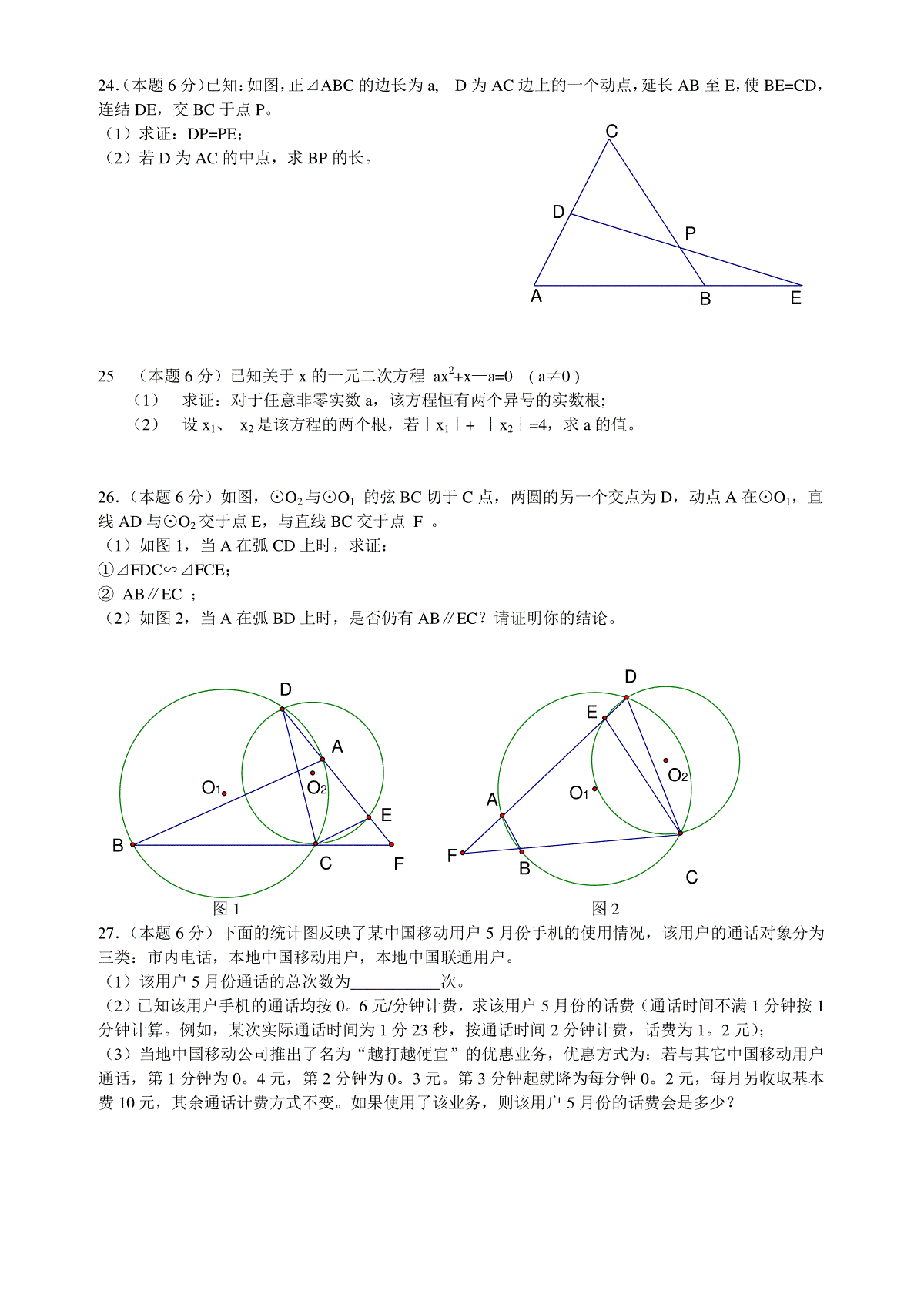
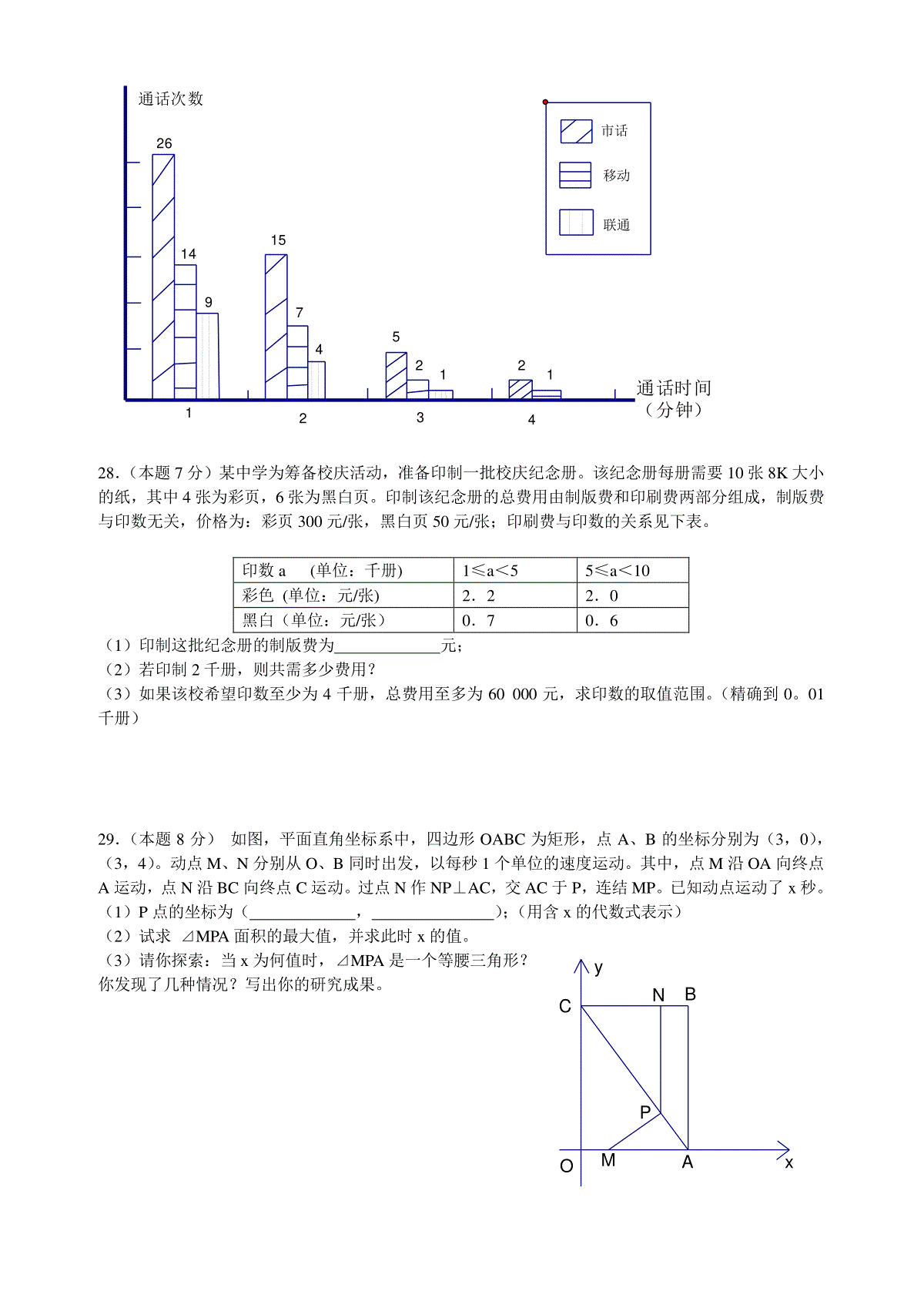
BCDAOABMABCDO2004年苏州市初中毕业暨升学考试试卷数学第一卷（选择题共30分）一选择题：本大题共10小题，每题3分，共30分。每小题给出的四个选项中，只有一个是符合题目要求的。1．下列运算正确的是（）Ａ。a5·a6=a30Ｂ.(a5)6=a30Ｃ.a5+a6=a11Ｄ.a5÷a6=562.观察下列中国传统工艺品的花纹，其中轴对称图形是（）３．如图，⊙Ｏ的半径为５，弦ＡＢ的长为８，Ｍ是弦ＡＢ上的动点，则线段ＯＭ长的最小值为（）Ａ。２Ｂ。３Ｃ。４Ｄ。５４．据有关资料，当前我国的道路交通安全形势十分严峻，去年我国交通事故的死亡人数约为１０。４万人，居世界第一，这个数用科学记数法表示是（）Ａ。1。04×104Ｂ1。04×105Ｃ1。04×106Ｄ10。4×1045．如图，矩形ABCD中，若AD=1，AB=3，则该矩形的两条对角线所成的锐角是（）A30°B45°C60°D75°6．已知正比例函数y=(3k—1)x，若y随x的增大而增大，则的取值范围是（）Ak＜0Bk＞0Ck＜31Dk＞317．西部山区某县响应国家“退耕还林”号召，将该县一部分耕地改还为林地。改还后，林地面积和耕地面积共有180km2,耕地面积是林地面积的25%。设改还后耕地面积为xkm2，林地面积为ykm2,则下列方程组中，正确的是（）Ａx+y=180Ｂ.x+y=180x=25%yy=25%xＣ.x+y=180Ｄ.x+y=180y—x=25%x-y=25%8.如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=Ａ。15°Ｂ。20°Ｃ。30°Ｄ。45°9．已知A=A0（1+mt）(m、A、A0均不为0)，则t=()OABCD125°ABCDCABDCBAＡ0AAmA.Ｂ.0AAmAＣ01AmAＤ00AAmA10．如图，梯形ABCD的对角线交于点O，有以下四个结论：①⊿AOB∽⊿COD②⊿AOD∽⊿ACB③S⊿DOC：S⊿AOD=DC：AB④S⊿AOD=S⊿BOC其中，始终正确的有（）A1个B2个C3个D4个第二卷（非选择题，共90分）二填空题（每小题3分，共24分）11．—31的绝对值是。12．函数y=3x中自变量x的取值范围是。13．如图，◇ABCD中，∠A=125°，∠B=度。14．为缓解苏州市区“打的难”的问题，今年市遗会前，苏州市区新增了出租车800辆，出租车的总量达到了3200辆。按市区人口216万来计算，扩容后苏州失市区每万人出租车拥有量可达到辆。（精确到0。1）15．如图，CD是Rt⊿ABC斜边AB上的中线，若CD=4，则AB=。16．若等腰三角形的腰长为4，底边长为2，则其周长为17已知（x1,y1），(x2,y2)为反比例函数xky图象上的点，当x1＜x2＜0时,y1＜y2,则k的一个值可为（只需写出符号条件的一个．．k的值）18．正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等。CBA20cm30cm—2—121—3—2--1321oyx三．解答题：本大题共11小题，共66分。解答应写出必要的计算过程、推演步骤或文字说明。19．（本题5分）不用计算器计算：12÷（—2）2—2-1+13120．（本题5分）化简：（)444222xxxx÷2xx21．（本题5分）解方程：212312xxxx。22．（本题6分）如图，苏州某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm.为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。（精确到1cm）23．（本题6分）如图，平面直角坐标系中画出了函数y=kx+b的图象。（1）根据图象，求k，b的值；（2）在图中画出函数y=—2x+2的图象；（3）求x的取值范围，使函数y=kx+b的函数值大于函数y=—2x+2的函数值。PEDCBAFEDCBAO1O2O2O1FEDCBA24．（本题6分）已知：如图，正⊿ABC的边长为a,D为AC边上的一个动点，延长AB至E，使BE=CD，连结DE，交BC于点P。（1）求证：DP=PE；（2）若D为AC的中点，求BP的长。25（本题6分）已知关于x的一元二次方程ax2+x—a=0(a≠0)（1）求证：对于任意非零实数a，该方程恒有两个异号的实数根;（2）设x1、x2是该方程的两个根，若∣x1∣+∣x2∣=4，求a的值。26．（本题6分）如图，⊙O2与⊙O1的弦BC切于C点，两圆的另一个交点为D，动点A在⊙O1，直线AD与⊙O2交于点E，与直线BC交于点F。（1）如图1，当A在弧CD上时，求证：①⊿FDC∽⊿FCE；②AB∥EC；（2）如图2，当A在弧BD上时，是否仍有AB∥EC？请证明你的结论。图1图227．（本题6分）下面的统计图反映了某中国移动用户5月份手机的使用情况，该用户的通话对象分为三类：市内电话，本地中国移动用户，本地中国联通用户。（1）该用户5月份通话的总次数为次。（2）已知该用户手机的通话均按0。6元/分钟计费，求该用户5月份的话费（通话时间不满1分钟按1分钟计算。例如，某次实际通话时间为1分23秒，按通话时间2分钟计费，话费为1。2元）；（3）当地中国移动公司推出了名为“越打越便宜”的优惠业务，优惠方式为：若与其它中国移动用户通话，第1分钟为0。4元，第2分钟为0。3元。第3分钟起就降为每分钟0。2元，每月另收取基本费10元，其余通话计费方式不变。如果使用了该业务，则该用户5月份的话费会是多少？PNMCBAOyx联通移动市话121254715914264321通话时间（分钟）通话次数28．（本题7分）某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。印数a(单位：千册)1≤a＜55≤a＜10彩色(单位：元/张)2．22．0黑白（单位：元/张）0．70．6（1）印制这批纪念册的制版费为元；（2）若印制2千册，则共需多少费用？（3）如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围。（精确到0。01千册）29．（本题8分）如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0），（3，4）。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥AC，交AC于P，连结MP。已知动点运动了x秒。（1）P点的坐标为（，）；（用含x的代数式表示）（2）试求⊿MPA面积的最大值，并求此时x的值。（3）请你探索：当x为何值时，⊿MPA是一个等腰三角形？你发现了几种情况？写出你的研究成果。答案：题号12345678910答案BABBCDACDC11）3112）x≥313)5514)14.8（注：精确度不对，扣1分）15)816)1017)答案不唯一，只要符合k＜0即可，如k=—1，或k=—2……。若答出k＜0，扣1分18）可以是：（注：画对一张图得2分，全对得3分）19）320）2xx21）x1=—1,x2=3122)AC的长度为222cm（最终结果中不含单位，扣1分）23）(1)k=1,b=2(2分)(2)图略（取对一点给1分，不列表不扣分。）（3）由题意，得x+2＞—2x+2∴x＞0(2分)24．（1）证明：过点D作DF∥AB，交BC于F（1分）∵⊿ABC为正三角形∴∠CDF=∠A=60°。∴⊿CDF为正三角形∴DF=CD又BE=CD，∴BE=DF（1分）又DF∥AB，∴∠PEB=∠PDF在⊿DFP和⊿EBP中，∠PEB=∠PDF∠BPE=∠FPDBE=FD∴⊿DFP≌⊿EBP。∴DP=PE（1分）（２）由（1）得⊿DFP≌⊿EBP，可得FP=BP（１分）∵Ｄ为ＡＣ中点，ＤＦ∥ＡＢ∴ＢＦ＝21ＢＣ＝21a（１分）∴ＢＰ＝21ＢＦ＝41a（１分）２５。（１）证明：∵⊿＝１＋4a2,∴⊿＞0∴方程恒有两个实数根(1分)设方程的两根为x1,x2,∵a≠0,∴x1·x2=—１＜０∴方程恒有两个异号的实数根（１分）（２）∵x1·x2＜０，∴∣x1∣＋∣x2∣＝∣x1—x2∣＝４（１分）x1＋x2（x1＋x2）2—４x1x2＝１６又∵x1＋x2＝—a1，（１分）∴21a＋４＝１６。∴a=±63(2分)２６。（１）证明：①∵ＢＣ为⊙Ｏ2的切线∴∠D=∠FCE（１分）又∠Ｆ＝∠Ｆ∴⊿ＦＤＣ∽⊿ＦＣＥ。（１分）②在⊙Ｏ1中，∠B＝∠D,(1分)又∠ＦＣＥ＝∠Ｂ。∴AB∥EC（１分）（２）仍有AB∥EC。（１分）∵ＡＢＣＤ是⊙Ｏ1的内接四边形，∴∠ＦＢＡ＝∠ＦＤＣ∵ＢＣ为⊙Ｏ2的切线，∴∠ＦＣＥ＝∠ＦＤＣ∴∠ＦＣＥ＝∠ＦＢＡ，∠∴AB∥EC。（１分）２７。解：（１）８６（次）（２分）（２）通话时间为：（２６＋１４＋９）＋（１５＋７＋４）×２＋（５＋２＋１）×３＋（２＋１）×４＝１３７（分钟）（１分）话费为：１３７×０。６＝８２。２（元）（１分）（３）使用新业务后，中国移动费用：（１４＋７＋２＋１）×０。４＋（７＋２＋１）×０。３＋（２＋１）×０。２＋１×０。２＝１３。４（元）（１分）市话费：（２６×１＋１５×２＋５×３＋２×４）×０。６＝４７。４（元）中国联通费用：（９x１＋４×２＋１×３）×０。６＝１２（元）合计话费为：１０＋１３。４＋４７。４＋１２＝８２。８（元）（１分）答：使用了新业务，则该用户5月份的话费会是８２。８（元）２８。解：（１）１５００（元）（２分）（２）若印制2千册，则印刷费为：（２.2×4+0.7×6）×2000=26000(元)（１分）∴总费用为：26000+1500=27500(元）（１分）(3)设印数为x千册，①若4≤x＜5，由题意，得1000×(2.2×4+0.7×6)x+1500≤60000解得x≤4。5（１分）∴4≤x≤４。5②若x≥５，由题意，得1000×(2.0×4+0.6×6)x+1500≤60000解得x≤5。04（１分）∴5≤x≤5。04综上所述，符合要求的印数x（千册）的取值范围为：4≤x≤４。5或5≤x≤5。04（１分）（如果少考虑等号成立情况，统扣１分）２９。解：（１）（3—x,34x）（１分+１分）(2)设⊿MPA的面积为S，在⊿MPA中，MA=3—x，MA边上的高为34x，其中，0≤x≤3.∴S=21（3—x）×34x（１分）=32(—x2+3x)=—32(x—23)2+23∴S的最大值为23（１分）此时x=23.（１分）(3)延长ＮＰ交x轴于Ｑ，则有ＰＱ⊥ＯＡ①若ＭＰ＝ＰＡ∵ＰＱ⊥ＭＡ∴ＭＱ＝ＱＡ＝x.∴3x=3,∴x=1（１分）②若ＭＰ＝ＭＡ，则ＭＱ＝3—2x，ＰＱ=34x，ＰＭ＝ＭＡ＝３—x在Ｒt⊿ＰＭＱ中，∵ＰＭ2＝ＭＱ2＋ＰＱ2∴(３—x)2=(3—2x)2+(34x)2∴x=4354（１分）③若ＰＡ＝ＡＭ，∵ＰＡ＝35x，ＡＭ＝３—x∴35x=３—x∴x=89（１分）综上所述，x=1，或x=4354，或x=89。（注：如果多解，统扣1分）∵