高中数学_二元一次不等式组表示平面区域课件_周一新人教A版必修5

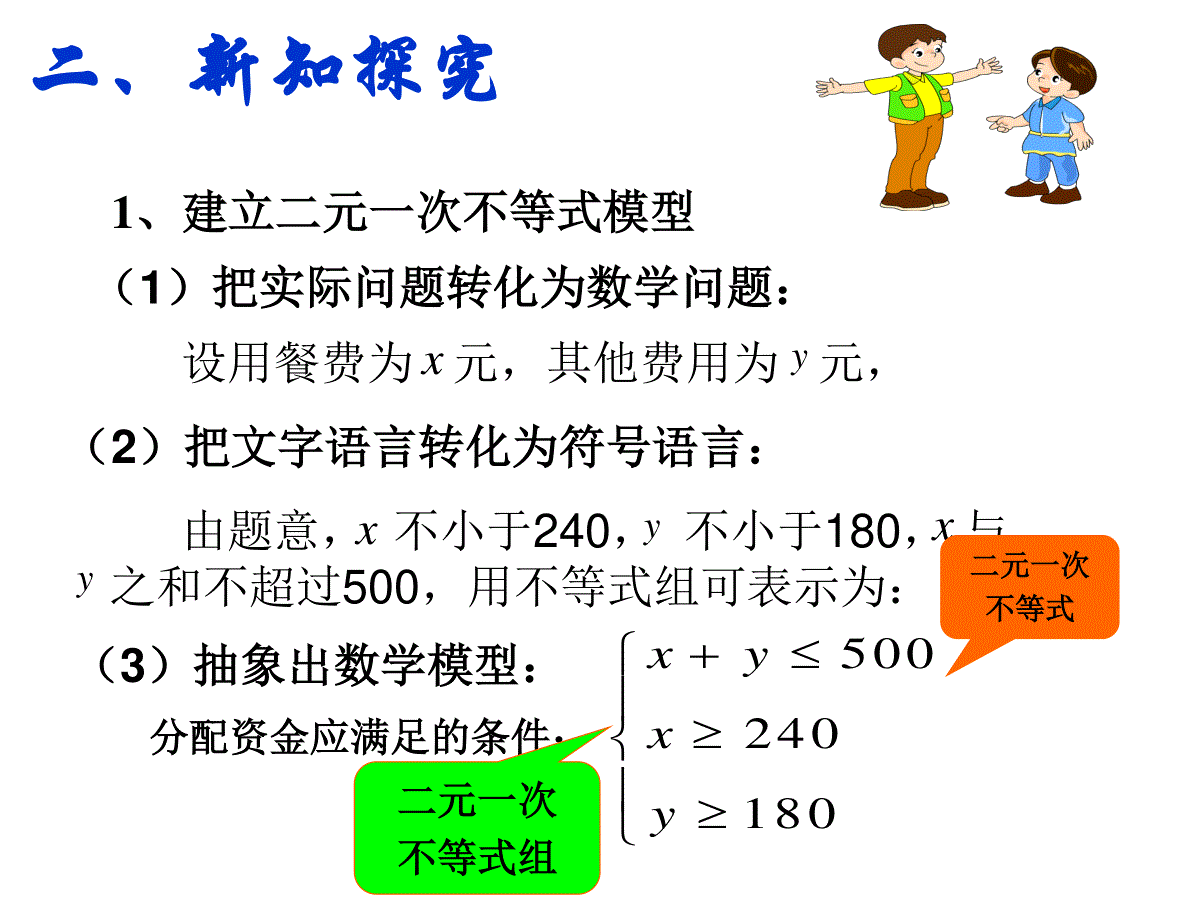
3.3.1二元一次不等式（组）与平面区域学习目标：1了解二元一次不等式的几何意义，会根据二元一次不等式确定它所表示的平面区域。2能用平面区域表示二元一次不等式组，能把若干直线围成的平面区域用二元一次不等式组表示。3能从实际情境中抽象出二元一次不等式组。4.通过画二元一次不等式（组）表示平面区域的过程，理解数形结合思想的应用。重点：理解如何用二元一次不等式（组）表示平面区域，能正确画出表示二元一次不等式（组）的平面区域；数形结合思想的应用。难点：如何确定二元一次不等式表示的平面区域。一、实例引入一名高中学生为自己制定的每月用餐费的最低标准是240元，又知其他费用的最少需支出180元，而每月可用来支配的资金为500元，这名学生可以如何使用这笔钱？问题：这个问题存在一些不等关系，应该用什么不等式模型来刻划它们呢？1、建立二元一次不等式模型二、新知探究（1）把实际问题转化为数学问题：yxyyx设用餐费为元，其他费用为元，（2）把文字语言转化为符号语言：由题意，不小于240，不小于180，与之和不超过500，用不等式组可表示为：x（3）抽象出数学模型：500240180xyxy分配资金应满足的条件：二元一次不等式二元一次不等式组2、定义（1）二元一次不等式：含有两个未知数，并且未知数的最高次数是1的不等式；（2）二元一次不等式组：由几个二元一次不等式组成的不等式组；探究：二元一次不等式（组）的解集满足二元一次不等式（组）的x和y的取值构成的有序实数对（x，y）集合，称为二元一次不等式（组）的解集。注意：二元一次不等式（组）的解集可以看成是直角坐标系内的点构成的集合。3、探究二元一次不等式（组）的解集表示的图形探究1：在直角坐标系内，二元一次不等式（组）的解集表示什么图形？如：不等式组0403xx的解集为数轴上的一个区间（如图）（1）回忆、思考回忆：一元一次不等式（组）的解集所表示的图形是——数轴上的区间。（2）探究Oxyx–y=6左上方区域右下方区域特殊：二元一次不等式x–y6的解集所表示的图形。作出的图像——6yx直线把平面分成三部分：左上方区域、右下方区域和直线上的点组成的图形一条直线不要忘了直线（2）探究验证：设点P（x，y1）是直线x–y=6上的点，选取点A（x，y2），使它的坐标满足不等式x–y6思考：①当点A与点P有相同的横坐标时，它们的纵坐标有什么关系？21yy②直线x–y=6左上方的点的坐标与不等式x–y6有什么关系？③直线x–y=6右下方点的坐标呢？的解！点都是的左上方的平面区域的反之，在直线的左上方的平面区域，都在直线的解为坐标的点：中6y不等式x6yx6yx6yx以二元一次不等式在平面直角坐标反之亦然。的右下方的平面区域，直线：的解为坐标的点都在以二元一次不等式：66yxyx在平面直角坐标系中，二元一次不等式x–y6的解为坐标的点都在直线x–y=6的左上方；反过来，直线x–y=6左上方的点的坐标都满足不等式x–y6。Oxyx–y=6结论思考:不等式呢?6yx结论：不等式x–y6表示直线x–y=6左上方的平面区域；不等式x–y6表示直线x–y=6右下方的平面区域；直线叫做这两个区域的边界。（3）从特殊到一般情况：二元一次不等式Ax+By+C＞0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。（虚线表示区域不包括边界直线）二元一次不等式表示相应直线的某一侧区域OxyAx+By+C=0结论一4．二元一次不等式表示哪个平面区域的判断方法直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同，只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C0表示直线的哪一侧区域，特别的，若C≠0时，常把原点（0，0）作为特殊点直线定界，特殊点定域。结论二例1：画出不等式x+4y4表示的平面区域x+4y-4=0解：(1)直线定界:先画直线x+4y–4=0（画成虚线）所以，原点在x+4y–40表示的平面区域内，不等式x+4y–40表示的区域如图所示。三、例题分析：(2)特殊点定域:取原点（0，0），代入x+4y-4，因为0+4×0–4=-40xyO41课堂练习:4x―3y-12=0x=1(1)画出不等式4x―3y≤12表示的平面区域(2)画出不等式x≥1表示的平面区域xy0xy0y-3x+12x2y的解集。例2、用平面区域表示不等式组0xy3x+y-12=0x-2y=0三、例题示范：练习．画出下列不等式组所表示的平面区域：21010xyxy≥解：（1）在同一个直角坐标系中，作出直线2x－y+1=0(虚线)，x+y－1=0(实线)。（2）分别作出不等式2x－y+10，x+y－1≥0所表示的平面区域，（3）则它们的交集就是已知不等式组所表示的区域。x+y-1=012-1-13212x-y+1=0Oyx（1）（2）232021030xyyx≥≤解：（1）在同一个直角坐标系中，作出直线2x－3y+2=0(虚线)，2y+1=0(实线)，x－3=0(实线)，（2）选点方法，分别作出不等式2x－3y+20，2y+1≥0，x－3≤0所表示的平面区域，（3）则它们的交集就是已知不等式组所表示的区域。2y+1=03x-3=0-212-1-13212x-3y+2=0Oy1．△ABC中，A(3，－1)，B(－1,1)，C(1,3)，写出△ABC区域所表示的二元一次不等式组．故x＋2y－1≥0；直线AC的方程为即2x＋y－5＝0，区域在直线AC的左下方(含边界)，故2x＋y－5≤0；解：直线AB的方程为：，即x＋2y－1＝0.如图，区域在直线AB的右上方(含边界)，直线BC的方程为：即x－y＋2＝0.区域在直线BC的右下方(含边界)，故x－y＋2≥0.所以△ABC的区域表示的二元一次不等式组为画平面区域的步骤：1：画线定界（注意虚实）；2：取点定侧；3：标明交点。（直线与直线的公共点）当堂训练：1、不等式x–2y+60表示的区域在直线x–2y+6=0的（）（A）右上方（B）右下方（C）左上方（D）左下方2、不等式3x+2y–6≤0表示的平面区域是（）BD当堂训练：3、不等式组B02063yxyx表示的平面区域是（）4.(21)(4)5.20,210210xyxyxyxyxy画出不等式0表示的平面区域。由直线和围成的三角形区域（包括边界）用不等式表示为：20210210xyxyxy注意：二元二次不等式常分解成两个二元一次因式乘积形式的不等式，它所表示的图形是两个对顶区域图形四、小结和作业作业：课本P93习题3.3[A组]第1、2题。⑴二元一次不等式表示平面区域：直线某一侧所有点组成的平面区域。⑵判定方法：直线定界，特殊点定域。小结：⑶二元一次不等式组表示平面区域：各个不等式所表示平面区域的公共部分。1知识点：2数学思想：数形结合