当前位置:首页 > 行业资料 > 国内外标准规范 > 2018年四川省凉山州中考数学试题
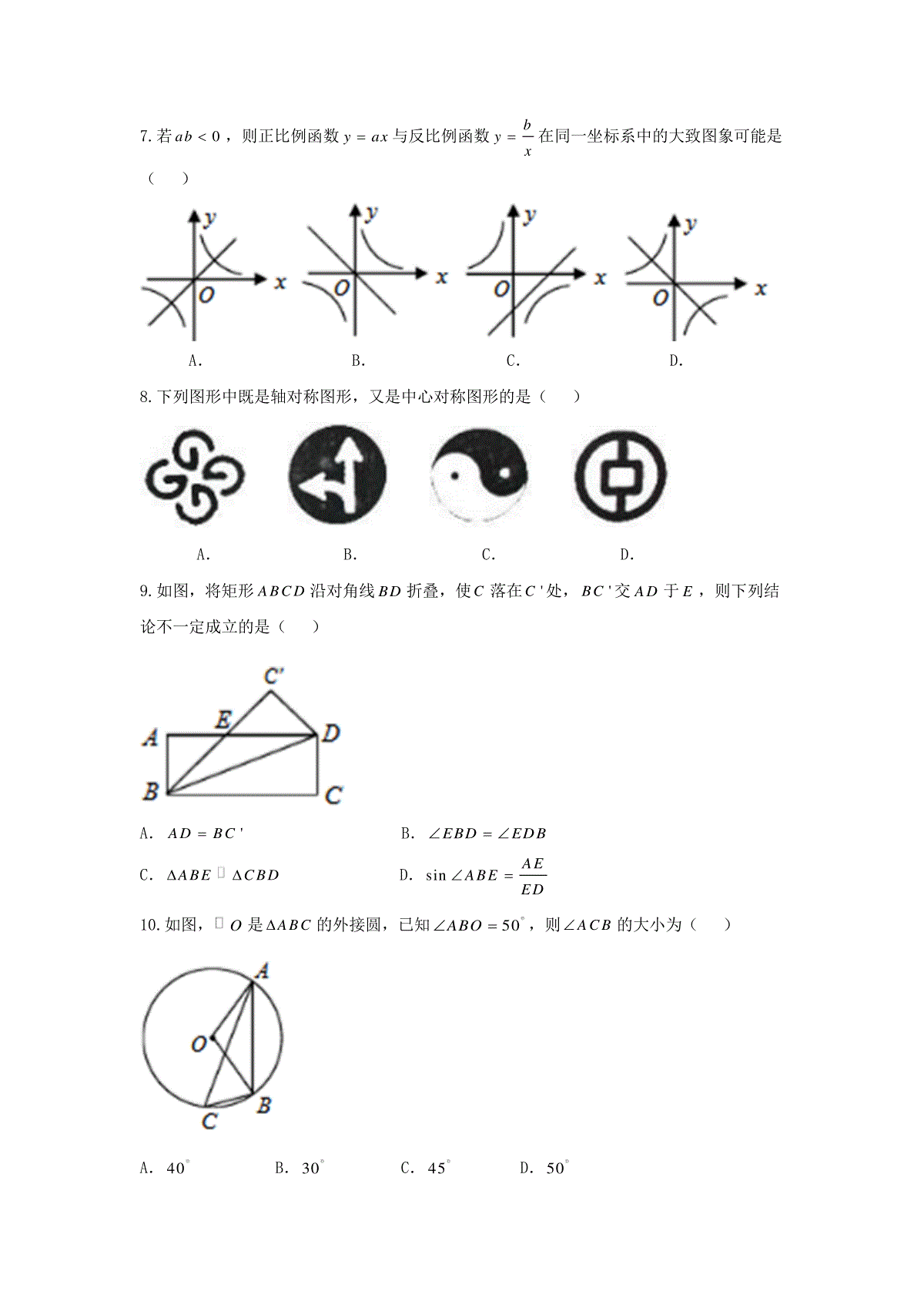
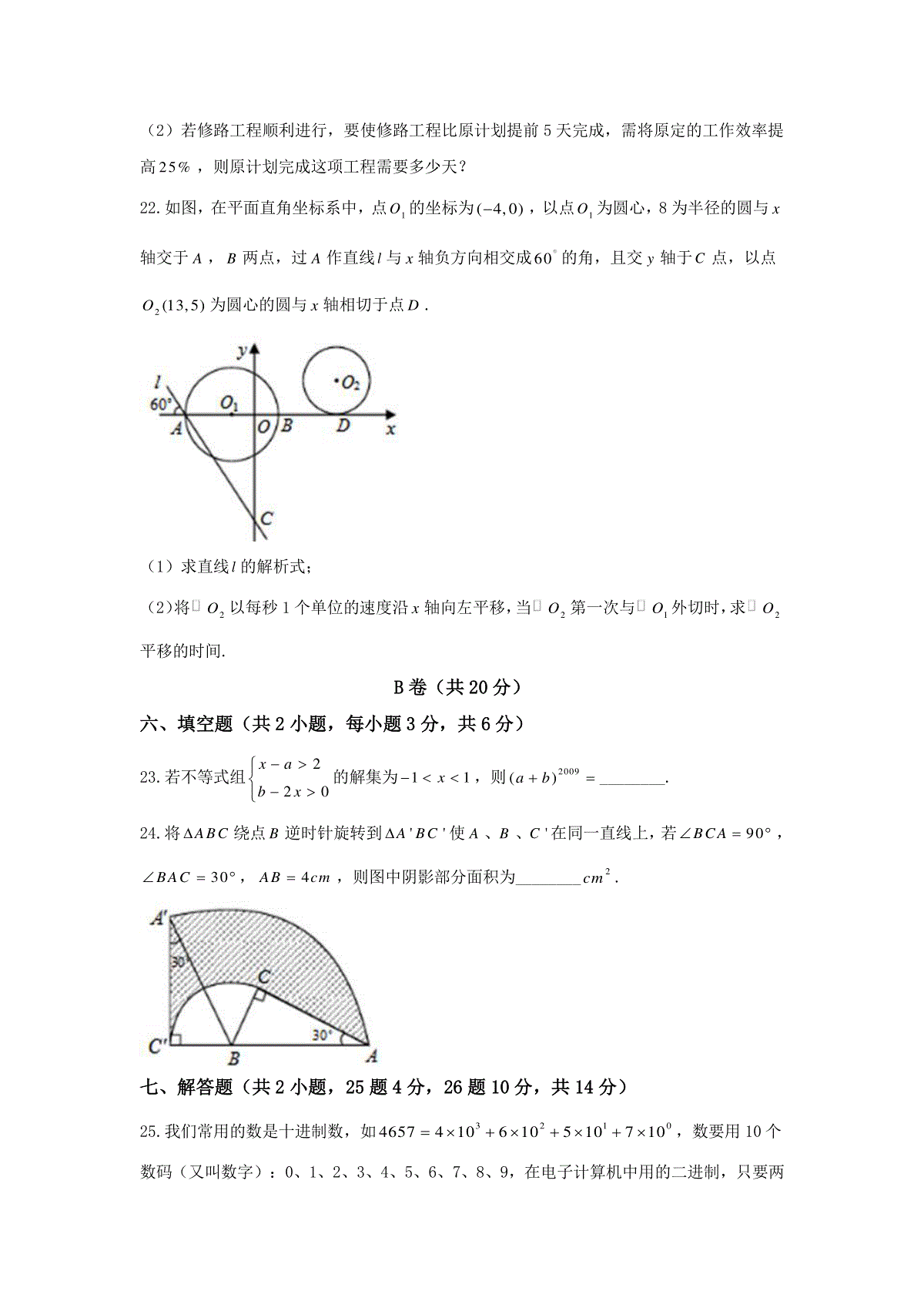
2018年凉山州初中毕业、高中阶段招生统一考试数学试卷A卷(共100分)第Ⅰ卷(选择题共30分)一、选择题(共10个小题,每小题3分,共30分)在每小题给出的四个选项中只有一项是正确的,请把正确选项的字母填涂在答题卡相应的位置.1.比1小2的数是()A.-1B.-2C.-3D.12.下列运算正确的是()A.3412aaaB.632aaaC.23aaaD.22(2)4aa3.长度单位1纳米910米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是()A.625.110米B.40.25110米C.52.5110米D.52.5110米4.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望小学时经过每个路口都是绿灯,但实际这样的机会是()A.12B.18C.38D.1112225.一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是()A.和B.谐C.凉D.山6.一组数据3、2、1、2、2的众数,中位数,方差分别是()A.2,1,0.4B.2,2,0.4C.3,1,2D.2,1,0.27.若0ab,则正比例函数yax与反比例函数byx在同一坐标系中的大致图象可能是()A.B.C.D.8.下列图形中既是轴对称图形,又是中心对称图形的是()A.B.C.D.9.如图,将矩形ABCD沿对角线BD折叠,使C落在'C处,'BC交AD于E,则下列结论不一定成立的是()A.'ADBCB.EBDEDBC.ABECBDD.sinAEABEED10.如图,O是ABC的外接圆,已知50ABO,则ACB的大小为()A.40B.30C.45D.502018年凉山州初中毕业、高中阶段招生统一考试数学试卷第Ⅱ卷(非选择题共70分)二、填空题(共4小题,每小题3分,共12分)11.分解因式39aa________,221218xx.12.已知'''ABCABC且''':1:2ABCABCSS,则:''ABAB.13.有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是.14.已知一个正数的平方根是32x和56x,则这个数是.三、解答题(共4小题,每小题7分,共28分)15.计算:033.143.1412cos45212009(21)(1).16.先化简,再选择一个你喜欢的数(要合适哦!)代入求值:2111xxx.17.观察下列多面体,并把下表补充完整.名称三棱柱四棱柱五棱柱六棱柱图形顶点数a61012棱数b912面数c58观察上表中的结果,你能发现a、b、c之间有什么关系吗?请写出关系式.18.如图,ABC在方格纸中.(1)请在方格纸上建立平面直角坐标系,使(2,3)A,(6,2)C,并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将ABC放大,画出放大后的图形'''ABC;(3)计算'''ABC的面积S.四、解答题(共2小题,每小题7分,共14分)19.我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)20.已知一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.(1)求从中随机抽取出一个黑球的概率是多少?(2)若往口袋中再放入x个白球和y个黑球,从口袋中随机取出一个白球的概率是14,求y与x之间的函数关系式.五、解答题(共2小题,每小题8分,共16分)21.如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45方向上,从A向东走600米到达B处,测得C在点B的北偏西60方向上.(1)MN是否穿过原始森林保护区?为什么?(参数数据:31.732)(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?22.如图,在平面直角坐标系中,点1O的坐标为(4,0),以点1O为圆心,8为半径的圆与x轴交于A,B两点,过A作直线l与x轴负方向相交成60的角,且交y轴于C点,以点2(13,5)O为圆心的圆与x轴相切于点D.(1)求直线l的解析式;(2)将2O以每秒1个单位的速度沿x轴向左平移,当2O第一次与1O外切时,求2O平移的时间.B卷(共20分)六、填空题(共2小题,每小题3分,共6分)23.若不等式组220xabx的解集为11x,则2009()ab________.24.将ABC绕点B逆时针旋转到''ABC使A、B、'C在同一直线上,若90BCA,30BAC,4ABcm,则图中阴影部分面积为________2cm.七、解答题(共2小题,25题4分,26题10分,共14分)25.我们常用的数是十进制数,如32104657410610510710,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中210110121202等于十进制的数6,543110101121202210120212等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?26.如图,已知抛物线2yxbxc经过(1,0)A,(0,2)B两点,顶点为D.(1)求抛物线的解析式;(2)将OAB绕点A顺时针旋转90后,点B落在点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;(3)设(2)中平移后,所得抛物线与y轴的交点为1B,顶点为1D,若点N在平移后的抛物线上,且满足1NBB的面积是1NDD面积的2倍,求点N的坐标.2018年凉山州初中毕业、高中阶段招生统一考试数学参考答案A卷(共100分)一、选择题1-5:ACDBD6-10:BBDCA二、填空题11.(3)(3)aaa22(3)x12.1:213.小林14.494三、解答题15.计算:原式(3.14)3.141212(1)221213.143.1421212211.16.解:2111(1)(1)1xxxxxxxx1(1)(1)xxxxx11x.取2x时,原式1121.17.名称三棱柱四棱柱五棱柱六棱柱顶点数a8棱数b1518面数c672acb.18.(1)画出原点O,x轴、y轴.(2,1)B.(2)画出图形'''ABC.(3)148162S.四、解答题19.解:设至少涨到每股x元时才能卖出.根据题意得1000(50001000)0.5%xx50001000,解这个不等式得1205199x,即6.06x.答:至少涨到每股6.06元时才能卖出.20.解:(1)取出一个黑球的概率44347P.(2)∵取出一个白球的概率37xPxy,∴3174xxy,∴1247xxy,∴y与x的函数关系式为:35yx.五、解答题21.(1)理由如下:如图,过C作CHAB于H,设CHx,由已知有45EAC,60FBC,则45CAH,30CBA,在RtACH中,AHCHx,在RtHBC中,tanCHHBCHB,∴3tan3033CHxHBx,∵AHHBAB,∴3600xx解得60022013x(米)200(米).∴MN不会穿过森林保护区.(2)解:设原计划完成这项工程需要y天,则实际完成工程需要(5)y天.根据题意得:11(125%)5yy,解得:25y,经检验知:25y是原方程的根,答:原计划完成这项工程需要25天.22.(1)解:由题意得4812OA,∴A点坐标为(12,0).∵在RtAOC中,60OAC,tan12tan60123OCOAOAC,∴C点的坐标为(0,123).设直线l的解析式为ykxb,由l过A、C两点,得123012bkb,解得1233bk,∴直线l的解析式为:3123yx.(2)如图,设2O平移t秒后到3O处与1O第一次外切于点P,3O与x轴相切于1D点,连接13OO,31OD.则13138513OOOPPO,∵31ODx轴,∴315OD,在131RtOOD中,222511133113512ODOOOD.∵1141317ODOOOD,∴111117125DDODOD,∴551t(秒),∴2O平移的时间为5秒.B卷(共20分)六、填空题23.-124.4七、解答题25.解:543101011120212210021212320802143.26.解:(1)已知抛物线2yxbxc经过(1,0)A,(0,2)B,∴01200bcc,解得32bc,∴所求抛物线的解析式为232yxx.(2)∵(1,0)A,(0,2)B,∴1OA,2OB,可得旋转后C点的坐标为(3,1).当3x时,由232yxx得2y,可知抛物线232yxx过点(3,2).∴将原抛物线沿y轴向下平移1个单位后过点C.∴平移后的抛物线解析式为:231yxx.(3)∵点N在231yxx上,可设N点坐标为2000(,31)xxx,将231yxx配方得23524yx,∴其对称轴为32x.①当0302x时,如图①,∵112NBBNDDSS,∴00113121222xx,∵01x,此时200311xx,∴N点的坐标为(1,1).②当032x时,如图②,同理可得0011312222xx,∴03x,此时200311xx,∴N点的坐标为(3,1).综上,点N的坐标为(1,1)或(3,1).



 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:2018年四川省凉山州中考数学试题
链接地址:https://www.777doc.com/doc-3728411 .html