2006-2017体育单招真题汇编-立体几何

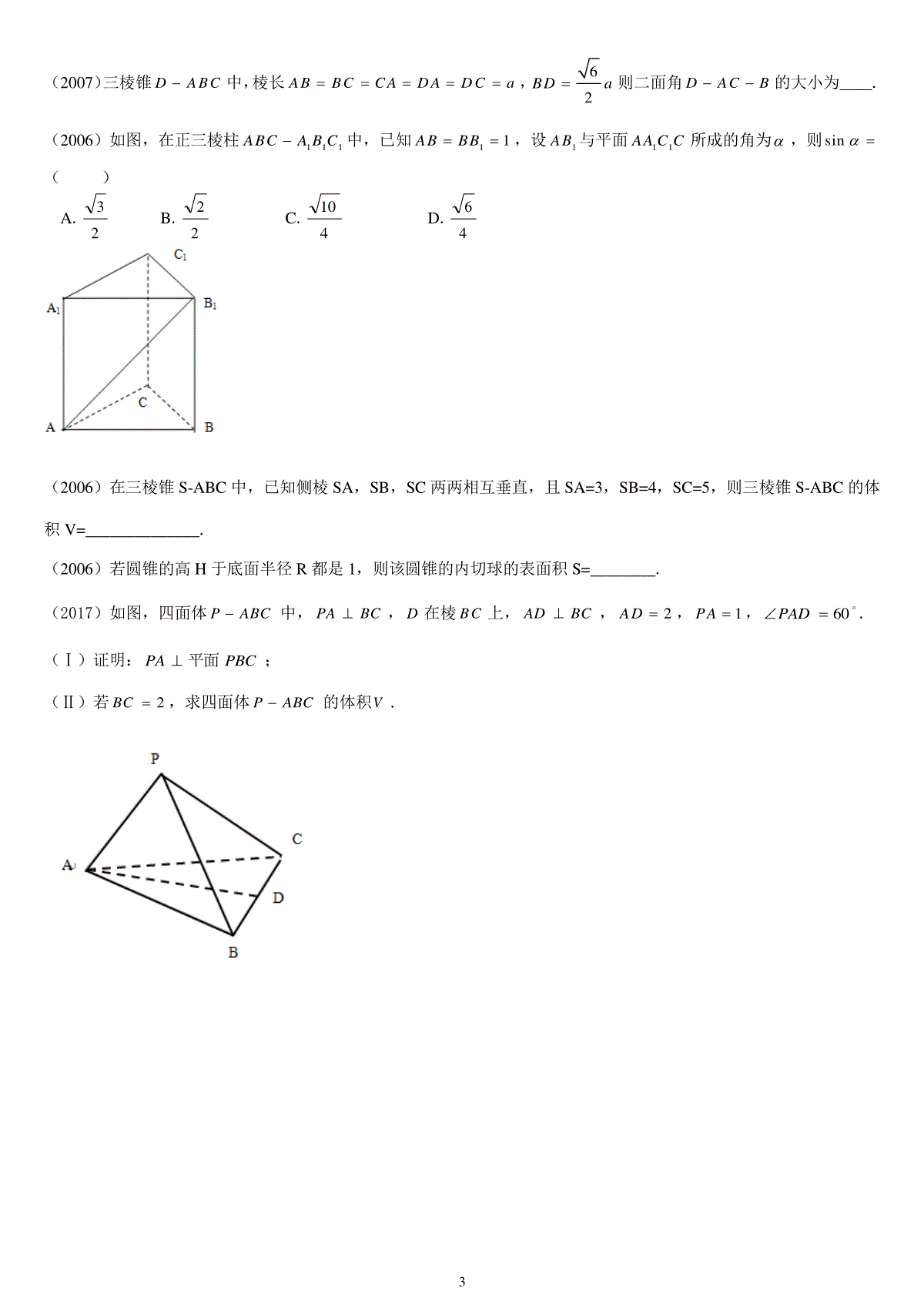
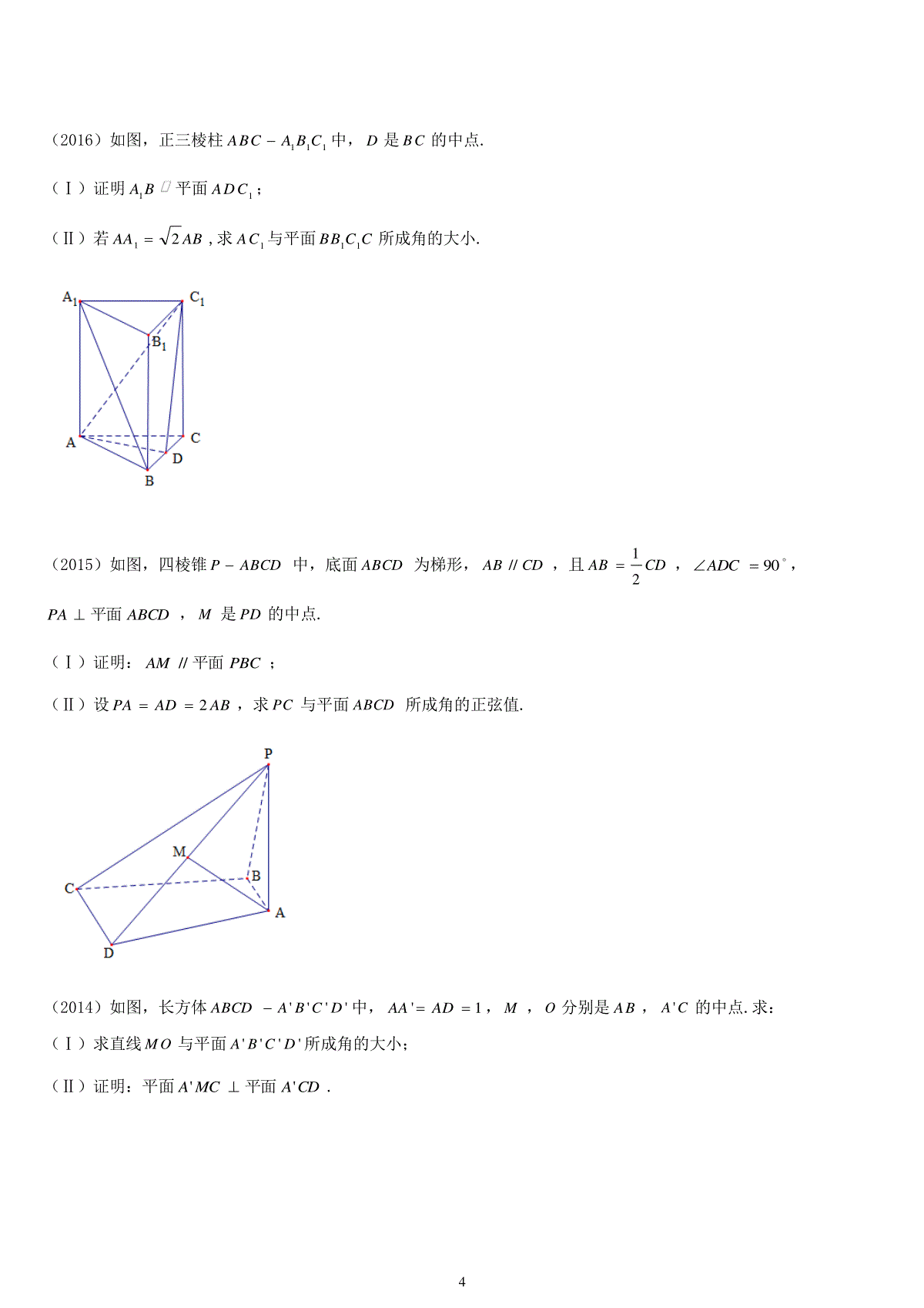
1历年体育单招真题汇编-立体几何（2017）点P在直二面角AB的交线AB上，C，D分别在,内，且4DPACPA，则CPD（）A.6B.4C.3D.2（2017）长方体''''DCBAABCD的长、宽、高分别为4，2，1，由顶点A沿长方体的表面到顶点'C路径长度的最小值为.（2016）两个球的表面积之比为1:4，则它们的体积之比为（）A.1:22B.1:4C.1:42D.1:8（2015）设直线l，m，平面，，有下列4个命题：①若l，m，则ml//②若//l，//m，则ml//③若l，l，则//④若//m，//m，则//其中的真命题是（）A.①③B.②③C.①④D.②④（2014）已知A，B为球O的球面上两点，平面AOB截球面所得圆上的劣弧AB长为10，且OBOA，则球O的半径等于（）A.40B.30C.20D.10（2013）若四面体的棱长都相等且它的体积为39a，则此四面体的棱长为（）A.32aB.2aC.32aD.329a（2013）已知圆锥的母线长为13，底面周长为10，则该圆锥侧面展开图的圆心角的弧度数为.（2012）下面是关于三个不同平面,,的四个命题1:p，∥；2:p∥，∥∥；3:p，；4:p，∥其中的真命题是（）A.12,ppB.34,ppC.13,ppD.24,pp（2012）已知圆锥侧面积是底面积的3倍，高为4cm，则圆锥的体积是cm3.（2011）已知圆锥曲线母线长为5，底面周长为6，则圆锥的体积是（）A.6B.12C.18D.36（2011）正三棱锥的底面边长为1，高为66，则侧面面积是.（2010）下面是关于两条直线m，n和两个平面，（m，n均不在，内）的四个命题：1:pm∥，n∥mn∥；2:pm∥，∥m∥；23:pm∥，n∥，∥mn∥；4:pmn∥，n，m∥其中的假命题是（）A.1p，3pB.1p，4pC.2p，3pD.2p，4p（2010）已知一个圆锥的母线长为13cm，高为12cm，则此圆锥的内切球的表面积Scm2，（轴截面如图所示）（2009）关于空间中的平面和直线m，n，l，有下列四个命题：1p：nmlnlm||,2p：nmnm||||,||3p：mllm,||4p：mlml相交与,其中真命题是（）A.1p，3pB.2p，4pC.3pD.4p（2009）表面积为180的球面上有A、B、C三点.已知AC=6，BC=8，AB=10，则球心到ABC所在平面的距离为___.（2008）正三棱锥的底面边长为2，体积为3，则正三棱锥的高是（）A.2B.3C.4D.6（2008）如图，正三棱柱'''CBAABC中，AB=1，AA'=2，则异面直线AB与A'C夹角的余弦值是.（2008）用平面截球，截得小圆的面积为，若球心到平面的距离为2，则球的表面积是.（2007）三个球的表面积之比为1:2:4，它们的体积依次为1V，2V，3V，则（）A.124VVB.1322VVC.234VVD.2322VV（2007）一个两头密封的圆柱形水桶装了一些水，当水桶水平横放时，桶内的水浸了水桶横截面周长的41.当水桶直立时，水的高度与桶的高度的比值是（）A.41B.4C.141D.21413（2007）三棱锥DABC中，棱长ABBCCADADCa，62BDa则二面角DACB的大小为____.（2006）如图，在正三棱柱111ABCABC中，已知11ABBB，设1AB与平面11AACC所成的角为，则sin（）A.23B.22C.410D.46（2006）在三棱锥S-ABC中，已知侧棱SA，SB，SC两两相互垂直，且SA=3，SB=4，SC=5，则三棱锥S-ABC的体积V=______________.（2006）若圆锥的高H于底面半径R都是1，则该圆锥的内切球的表面积S=________.（2017）如图，四面体ABCP中，BCPA，D在棱BC上，BCAD，2AD，1PA，60PAD.（Ⅰ）证明：PBCPA平面；（Ⅱ）若2BC，求四面体ABCP的体积V.4（2016）如图，正三棱柱111ABCABC中，D是BC的中点.（Ⅰ）证明1AB平面1ADC；（Ⅱ）若ABAA21,求1AC与平面11BBCC所成角的大小.（2015）如图，四棱锥ABCDP中，底面ABCD为梯形，CDAB//，且CDAB21，90ADC，ABCDPA平面，M是PD的中点.（Ⅰ）证明：PBCAM平面//；（Ⅱ）设ABADPA2，求PC与平面ABCD所成角的正弦值.（2014）如图，长方体''''DCBAABCD中，1'ADAA，M，O分别是AB，CA'的中点.求：（Ⅰ）求直线MO与平面''''DCBA所成角的大小；（Ⅱ）证明：平面CDAMCA''平面.5（2013）如图，已知长方体1111ABCDABCD中，6AB，4BC，13AA，M为AB的中点.求：（Ⅰ）二面角111MBCA的大小；（Ⅱ）点1D到平面11MBC的距离.（2012）如图，已知正方形1111ABCDABCD的棱长为1，M是11BD的中点.（Ⅰ）证明BMAC；（Ⅱ）求异面直线BM与1CD的夹角；（Ⅲ）求点B到平面1ABM的距离.6（2011）如图正方体''''DCBAABCD中，P是线段AB上的点，1AP，3PB.（Ⅰ）求异面直线PB'与BD的夹角的余弦值；（Ⅱ）求二面角BPCB'的大小；（Ⅲ）求点B到平面PCB'的距离.（2010）如图，长方体1111ABCDABCD中，E为11AC中点，已知2ABBC，二面角1ABDC的大小为4π3.（Ⅰ）求1AA的长；（Ⅱ）证明：AE平面ABD；（Ⅲ）求异面直线AE与BC所成角的大小.7（2009）正三棱柱111ABCABC，已知1AB，D为11CA的中点.（Ⅰ）证明：BA1||平面CDB1；（Ⅱ）当231AA时，求点1B到平面11BCA的距离；（Ⅲ）1AA取什么值时，二面角BCAB111的大小为6.（2008）如图，直三棱柱ABCA'B'C'中，2AC，1BCBB'，ABC是直角，M是BB'的中点.（Ⅰ）求平面AMC'与平面A'B'C'所成二面角的平面角的大小；（Ⅱ）求点B'到平面AMC'的距离.8（2007）已知ABCA'B'C'为正三棱柱，D是BC中点.（Ⅰ）证明A'B平面ADC'；（Ⅱ）若AA'AB，求A'B与平面AA'C'C所成角的大小；（Ⅲ）若ABa，当A'A等于何值时A'BAC'？证明你的结论.（2006）如图，在长方体1111ABCDABCD中，已知2ABBC，13AA，点O是正方形1111ABCD的中心，点P在棱1CC上，且1CP.（Ⅰ）求直线AP与平面11BCCB所成角的正弦值；（Ⅱ）求点P到平面11ABCD的距离；（Ⅲ）设点O在平面1APD上的投影是H，证明1APDH.专注体育特长生辅导12年，微信：gxhua2004