2014届高三数学(文)一轮总复习平面向量基本定理及其坐标表示

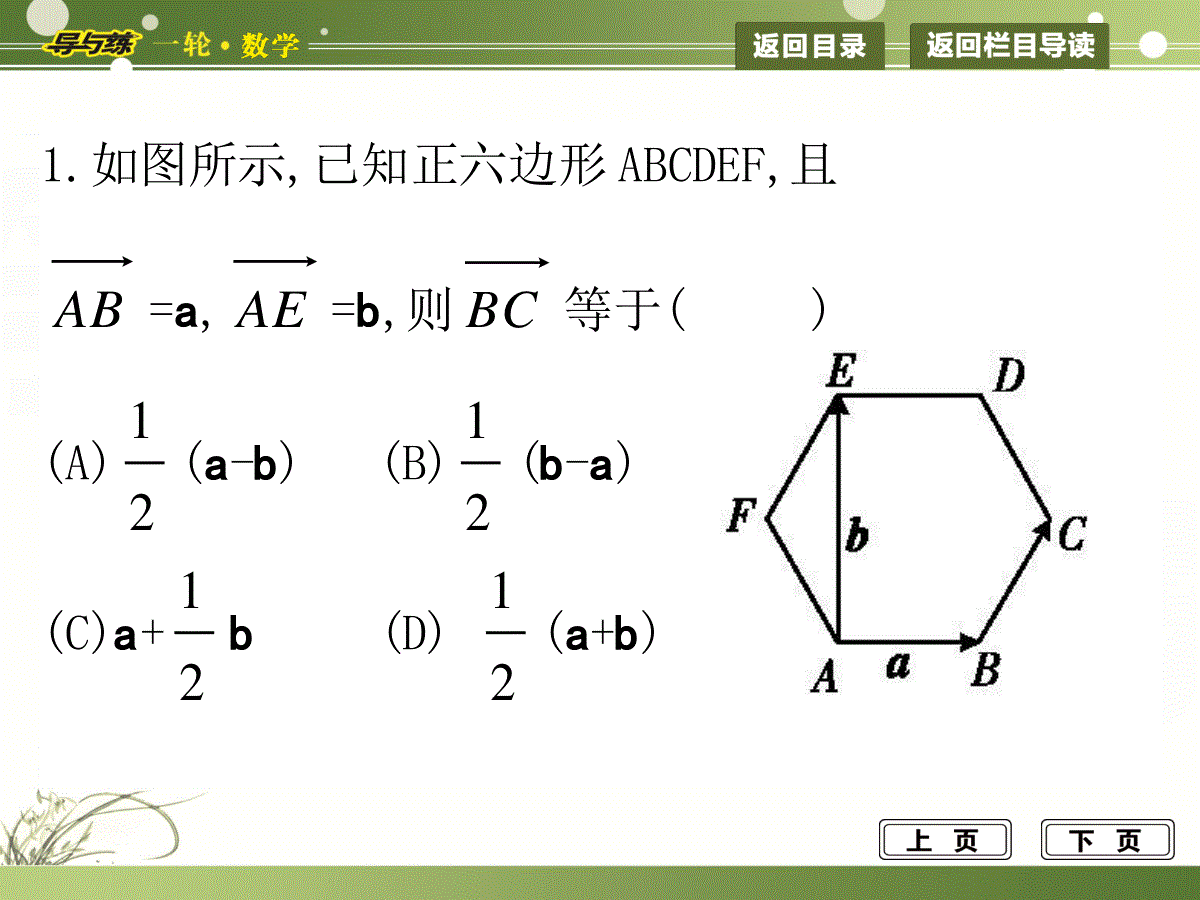
基础自主梳理考向互动探究第节平面向量基本定理及其坐标表示最新考纲1.了解平面向量的基本定理.2.掌握平面向量的正交分解及其坐标表示.3.会用坐标表示平面向量的加法、减法与数乘运算.4.理解用坐标表示的平面向量共线的条件.1.如图所示,已知正六边形ABCDEF,且AB=a,AE=b,则BC等于(D)(A)21(a-b)(B)21(b-a)(C)a+21b(D)21(a+b)解析:∵AB+AE=a+b=AD,由题意知BC=21AD,∴BC=21(a+b),故选D.2.(2012年高考广东卷)若向量AB=(1,2),BC=(3,4),则AC等于(A)(A)(4,6)(B)(-4,-6)(C)(-2,-2)(D)(2,2)解析:AC=AB+BC=(1,2)+(3,4)=(4,6),故选A.3.若向量a=(1,1),b=(-1,1),c=(4,2),则c等于(用a,b表示).解析:设c=ma+nb,则(4,2)=m(1,1)+n(-1,1)得，nm，nm24解得，n，m13所以c=3a-b.答案:3a-b4.已知a=(1,2),b=(x,1),且a+2b与2a-b平行,则x等于.解析:∵a=(1,2),b=(x,1),∴a+2b=(1,2)+2×(x,1)=(2x+1,4),2a-b=2×(1,2)-(x,1)=(2-x,3).∵a+2b与2a-b平行,∴(2x+1)×3-4×(2-x)=0,解之,得x=21.答案:211.平面向量基本定理(1)条件:e1,e2是同一平面内的两个不共线向量.结论:对于这一平面内任意向量a,有且只有一对实数λ1、λ2,使a=λ1e1+λ2e2.(2)关于平面向量基本定理的几点说明:①e1、e2均为非零向量,且不共线,它们是这一平面内所有向量的一组基底.②基底不唯一,当基底给定时,分解形式唯一:λ1、λ2是被a、e1、e2唯一确定的数量.③由定理可将任一向量a在给出基底e1、e2的条件下进行分解;同一平面内任一向量都可以表示为两个不共线向量的线性组合.④λ2=0时,a与e1共线;λ1=0时,a与e2共线;λ1=λ2=0时,a=0.质疑探究1:已知两个不共线的向量e1,e2为平面内所有向量的一组基底,可以表示出平面向量a,b,那么一定能用a,b作为平面内所有向量的一组基底吗?为什么?提示:不一定,用不共线向量e1,e2表示的向量a,b可能共线,也可能不共线,当a与b共线时不能,如a=e1+23e2,b=2e1+3e2.2.平面向量的正交分解与坐标表示(1)平面向量的正交分解把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.(2)平面向量的坐标表示在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得a=xi+yj,这样,平面内的任一向量a都可由x、y唯一确定,因此把(x,y)叫做向量a的坐标,记作a=(x,y),其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.3.平面向量的坐标运算(1)若a=(x1,y1),b=(x2,y2),则a±b=(x1±x2,y1±y2);(2)若A(x1,y1),B(x2,y2),则AB=(x2-x1,y2-y1);(3)若a=(x,y),则λa=(λx,λy);(4)若a=(x1,y1),b=(x2,y2),则a=b⇔；2121yy，xx(5)若a=(x1,y1),b=(x2,y2),则a∥b⇔x1y2-x2y1=0.质疑探究2:相等向量的坐标一定相同吗?相等向量起点和终点坐标可以不同吗?提示:一定相同.可以不同.例如A(3,5),B(6,8),AB=(3,3);C(-5,3),D(-2,6),CD=(3,3),显然AB=CD,但A、B、C、D四点坐标各不相同.平面向量基本定理及其应用【例1】(2012南京质检)如图所示,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若AM=λAB+μAC,则λ+μ=.思维导引:由于B、H、C三点共线,可用AB、AC来表示AH,从而求得AM与AB、AC的关系.解析:由B、H、C三点共线,可设BH=xHC(x0),∴AH-AB=x(AC-AH),AH=xx1AC+x11AB,又由M为AH的中点知AM=21AH=）1（2xxAC+）1（21xAB,又∵AM=λAB+μAC,∴λ+μ=）1（21x+）1（2xx=21.答案:21平面向量基本定理表明,平面内任意一个向量都可以用一组基底唯一表示,也就是利用已知向量表示未知向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算.具体问题中可结合图形进行思考、分析转化..变式训练1-1:设e1,e2是两个不共线的向量,且a=e1+λe2与b=-31e2-e1共线,则实数λ等于()(A)-1(B)3(C)-31(D)31解析:因为a=e1+λe2与b=-31e2-e1共线,所以存在实数t,使得b=ta,即-31e2-e1=t(e1+λe2),-31e2-e1=te1+tλe2,所以t=-1,tλ=-31,即λ=31.故选D.平面向量的坐标运算【例2】已知A(2,3)、B(5,4)、C(7,10).(1)求AB;(2)若AB=mAC+nBC,求m、n.解:(1)由题意A(2,3)、B(5,4),所以AB=(3,1).(2)由于AB=(3,1),AC=(5,7),BC=(2,6),所以(3,1)=m(5,7)+n(2,6),得,167,325nmnm解得,1,1nm两向量a=(x1,y1),b=(x2,y2)相等的充要条件是它们的对应坐标分别相等,即，，2121yyxx利用向量相等可列出方程组,求其中的未知量,从而解决求字母取值、求点的坐标及向量的坐标等问题.变式训练2-1:设两个向量a=(λ+2,λ2-cos2α)和b=(m,2m+sinα),其中λ、m、α为实数,若a=2b,则m的取值范围是()(A)[-6,1](B)[4,8](C)(-6,1](D)[-1,6]解析:根据已知条件得2b=(2m,m+2sinα),又a=2b,所以λ+2=2m,λ2-cos2α=m+2sinα,于是2λ2-2cos2α=λ+2+4sinα,即2λ2-λ=-2sin2α+4sinα+4=-2(sinα-1)2+6,故-2≤2λ2-λ≤6,即622222解得-23≤λ≤2,故m=12=2-24∈[-6,1],故选A.平面向量共线的坐标表示【例3】平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).(1)求满足a=mb+nc的实数m、n;(2)若(a+kc)∥(2b-a),求实数k.解:(1)由题意得(3,2)=m(-1,2)+n(4,1),所以,22,34nmnm得,98,95nm(2)a+kc=(3+4k,2+k),2b-a=(-5,2),由题意得2×(3+4k)-(-5)×(2+k)=0.∴k=-1316.如果已知两向量共线,求某些参数的取值时,则利用“若a=(x1,y1),b=(x2,y2),则a∥b的充要条件是x1y2=x2y1”解题比较方便.变式训练31:已知平面向量a=(1,-m),b=(m2,m),则向量a+b()(A)平行于x轴(B)平行于第一、三象限的角平分线(C)平行于y轴(D)平行于第二、四象限的角平分线解析:a+b=(1,-m)+(m2,m)=(1+m2,0),其横坐标恒大于零,纵坐标为零,向量a+b平行于x轴,故选A.变式训练32:(2012盐城质检)△ABC中,内角A、B、C所对的边分别为a、b、c,若p=(a+c,b),q=(b-a,c-a),且p∥q,则角C=.解析:因为p∥q,则(a+c)(c-a)-b(b-a)=0,所以a2+b2-c2=ab,所以abcba2222=21,结合余弦定理知,cosC=21,又0°C180°,∴C=60°.答案:60°【例1】在△ABC中,B、C点的坐标分别为B(-1,2),C(3,4),且AB-2BC=(-1,3),则A点的坐标为()(A)(0,0)(B)(-4,5)(C)(-3,-6)(D)(-8,-5)解析:设A点的坐标为A(x,y),由已知B(-1,2),C(3,4),且AB-2BC=(-1,3),所以(-1-x,2-y)-2(3+1,4-2)=(-1,3),即(-1-x,2-y)=(7,7),所以x=-8,y=-5.故选D.【例2】(2012镇江模拟)已知点O为坐标原点,A(0,2),B(4,6),OM=t1OA+t2AB.(1)求点M在第二或第三象限的充要条件;(2)求证:当t1=1时,不论t2为何实数,A、B、M三点都共线;(3)若t1=a2,求当OMAB且△ABM的面积为12时a的值.(1)解:OM=t1OA+t2AB=t1(0,2)+t2(4,4)=(4t2,2t1+4t2).当点M在第二或第三象限时,有,042,04212ttt故所求的充要条件为t20且t1+2t2≠0.(2)证明:当t1=1时,由(1)知OM=(4t2,4t2+2).∵AB=OB-OA=(4,4),AM=OM-OA=(4t2,4t2)=t2(4,4)=t2AB,∴当t1=1时,不论t2为何实数,A、B、M三点都共线.(3)解:当t1=a2时,OM=(4t2,4t2+2a2).又AB=(4,4),OMAB,∴4t2×4+(4t2+2a2)×4=0,∴t2=-41a2,故OM=(-a2,a2).又|AB|=42,点M到直线AB:x-y+2=0的距离d=2|2|22aa=2|a2-1|.∵S△ABN=12,∴21|AB|·d=21×42×2|a2-1|=12,解得a=±2,故所求a的值为±2.点击进入限时训练