定点线与抛物线相交问题引发的探究与思考

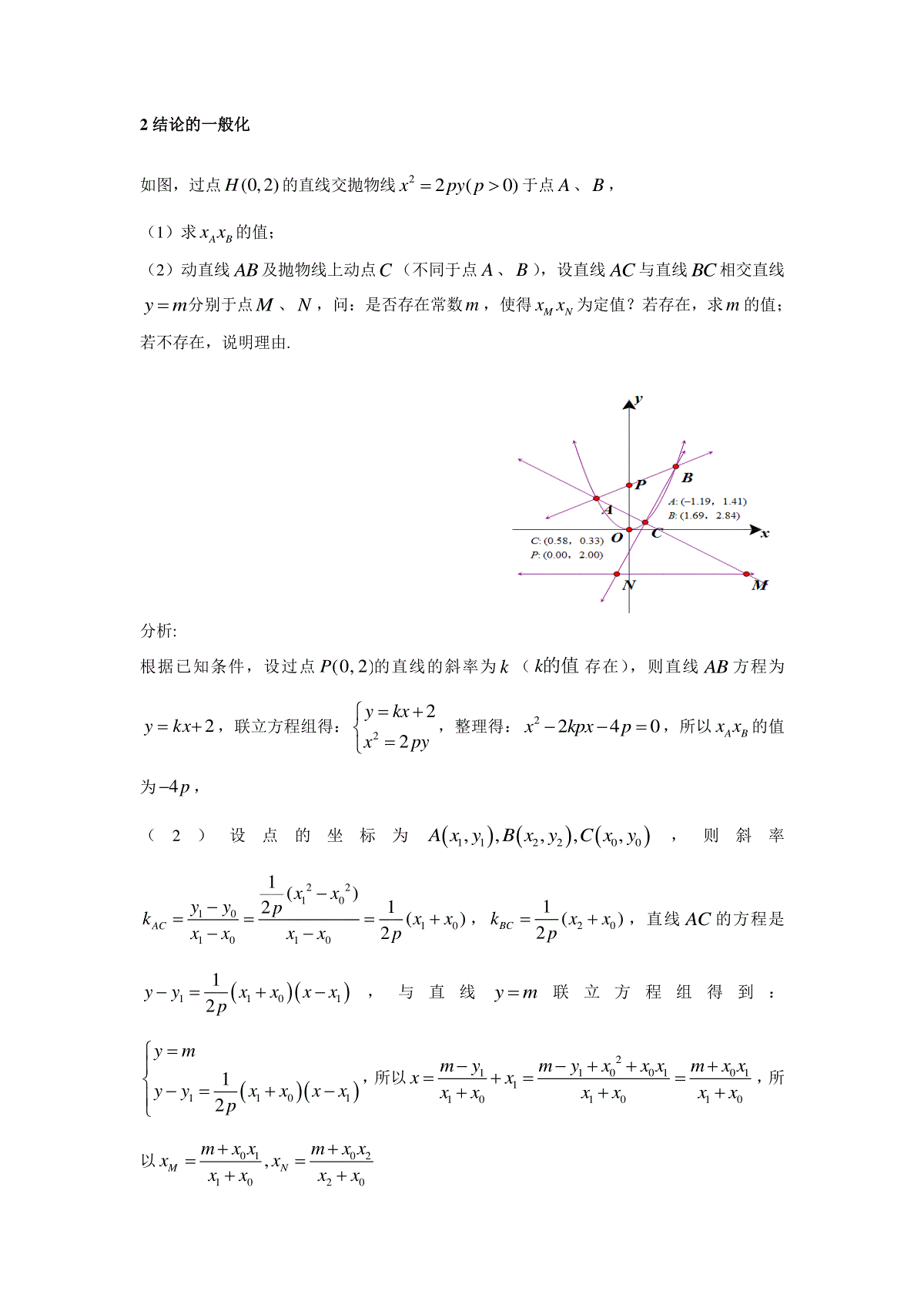
定点线与抛物线相交问题引发的探究与思考浙江省永嘉中学(325100)赵万双【背景】2013年浙江省学业水平考试已结束，数学试卷第41题留给我们的思考却远未停止，研究该题可以指导我们今后的复习工作。考后本人对两个班级的学生成绩作了统计，该题得分率只有0.45，针对原题结论结合学生解题情况，本文从不同视角、一般化归、类比推导、原因分析、引申拓展等几个方面对该题进行探究，得出了定点线与圆锥曲线相交时的定值结论。1原题呈现如图，过点(0,2)P的直线交抛物线2yx于点A、B，（1）求ABxx的值；（2）动直线AB及抛物线上动点C（不同于点A、B），设直线AC与直线BC相交直线ym分别于点M、N，问：是否存在常数m，使得MNxx为定值？若存在，求m的值；若不存在，说明理由.（1）分析：根据已知条件，设过点(0,2)P的直线的斜率为k（k的值存在），则直线AB方程为2ykx，联立方程组得：22ykxyx，整理得：220xkx，所以ABxx的值为2，视角1：设点的坐标为112200,,,,,AxyBxyCxy，则斜率221010101010ACyyxxkxxxxxx，20BCkxx，直线AC的方程是1101yyxxxx，与直线ym联立方程组得到：1101ymyyxxxx，x所以210010111101010myxxxmxxmyxxxxxxxx，所以01021020,MNmxxmxxxxxxxx所以01020102MNmxxmxxxxxxxx=220120122012012mmxxxxxxxxxxxx=220020022mmkxxxkx，当224mm，得到2m时，使得2MNxx.视角2：向量法设点的坐标为,,,MNMxmNxm，mxmxONOMNM,,=2mxxNM，由方法1可知：01021020,MNmxxmxxxxxxxx，所以0102220102MNmxxmxxxxmmxxxx=220120122012012mmxxxxxxxxxxxx+2m=220020022mmkxxxkx+2m=2)(2020202220kxxmxmkkmxm，当22222mmmm时，解得2m，使得2MNxx.视角3：共线法设点的坐标为1100,,,AxyCxy，mxMM,，点MCA,,共线，所以AMACkk，221010101010ACyyxxkxxxxxx，020xxxmkMAM，020xxxmM=01xx，01020xxxxxmM=101200xxxxxxxMM，01021020,MNmxxmxxxxxxxx，所以01020102MNmxxmxxxxxxxx=220120122012012mmxxxxxxxxxxxx=220020022mmkxxxkx，当224mm，得到2m时，使得2MNxx.思考:在不同视角下为何只存在一个值2m,使得2MNxx.m的取值是否与点P的坐标0,2有关系呢?2结论的一般化如图，过点(0,2)H的直线交抛物线22(0)xpyp于点A、B，（1）求ABxx的值；（2）动直线AB及抛物线上动点C（不同于点A、B），设直线AC与直线BC相交直线ym分别于点M、N，问：是否存在常数m，使得MNxx为定值？若存在，求m的值；若不存在，说明理由.分析:根据已知条件，设过点(0,2)P的直线的斜率为k（k的值存在），则直线AB方程为2ykx，联立方程组得：222ykxxpy，整理得：2240xkpxp，所以ABxx的值为4p，（2）设点的坐标为112200,,,,,AxyBxyCxy，则斜率2210101010101()12()2ACxxyypkxxxxxxp，201()2BCkxxp，直线AC的方程是110112yyxxxxp，与直线ym联立方程组得到：110112ymyyxxxxp，所以210010111101010myxxxmxxmyxxxxxxxx，所以01021020,MNmxxmxxxxxxxx所以01020102MNmxxmxxxxxxxx=220120122012012mmxxxxxxxxxxxx=220020022mmkxxxkx，当224mm，得到2m时，使得2MNxx.点评:本题主要考查抛物线的标准方程及几何性质、直线与抛物线的位置关系等,旨在考查考生综合应用知识的能力.结论中为什么存在常数2m（与p的取值无关），与定点0,2有一定关系，m的取值与定点0,a中a的值有着怎么样的关系呢？,为了得出科学的结论,大胆做出更一般化推导3类比推导如图，过点(,0)a0a的直线交抛物线22(0)ypxp于点A、B，（1）求AByy的值；（2）动直线AB及抛物线上动点C（不同于点A、B），设直线AC与直线BC相交直线xm分别于点M、N，问：是否存在常数m，使得MNyy为定值？若存在，求m的值；若不存在，说明理由.分析:根据已知条件，设过点(,0)a的直线的斜率为k（k的值存在），则直线AB方程为()ykxa0k，联立方程组得：2()2ykxaypx，整理得：220yypak，所以2220pyypak，AByy的值为2pa（定值）108642246551015F:(–1.00,0.00)FNMOABC（2）设点的坐标为112200,,,,,AxyBxyCxy，则斜率10102210101021()2ACyyyypkxxyyyy，202BCpkyy，直线AC的方程是11102pyyxxyy，与直线xm联立方程组得到：11102xmpyyxxyy，所以11102()Mpymxyyy211011022pmypxyyyy01102pmyyyy，所以02202Npmyyyyy所以0102010222MNpmyypmyyyyyyyy222012012201201242pmpmyyyyyyyyyyyy22220020044222ppmmypaykpyypak，当2222pmpama，得到ma时，存在直线xa（仅与定点有关），使得2MNyypa.结论：常数ma的值与p离心率的取值无关，为什么仅与定点P的坐标有关系呢？把结论更一般化分析。4定值原因分析如图，过点(0,)a的直线交抛物线22(0)xpyp于点A、B，（1）求ABxx的值；（2）动直线AB及抛物线上动点C（不同于点A、B），设直线AC与直线BC相交直线ym分别于点M、N，问：是否存在常数m，使得MNxx为定值？若存在，求m的值；若不存在，说明理由.分析：1、设点1122,,,AxyBxy，抛物线的顶点的坐标是0,0O，连接直线,OAOB，则斜率之积OAOBkk1212yyxx12214xxp，经过定点(0,)a的直线交抛物线22(0)xpyp于点A、B，点A、B在抛物线上任意移动及抛物线上任意动点C（不同于点A、B），斜率之积OAOBkk始终是一个定值.所以才有ABxx的值是一个定值.存在一个ma,存在直线ya（仅与定点有关），使得2MNxxpa.2、点N关于原点对称点是S，点M关于原点对称点是T，所以MNSTxxxx，BATSxxxx，2ABxxpa，PSy轴，根据已知条件，设过点(,0)a的直线的斜率为k（k的值存在），则直线AB方程为0ykxak，PSI与PRB相似，RBSIPRPS，mxSN,，akxxB22,，makxxR22,，所以22xxmakxmakxNN，02xxmaN，只需am，存在直线ya（仅与定点有关），使得2MNxxpa.5原题引申在椭圆22221(0)xyabab中,点,AB是它的左右顶点,点C(不同于点,AB)是椭圆上的任意一点,连接直线,CACB,不难发现斜率之积CACBkk22ba(定值),如果直线,CACB与直线xm分别相交于点M,N,是否存在常数m的值，使得MNyy为定值？若存在，求m的值；若不存在，说明理由.分析：设点00,0,,0,,AaBaCxy,(0xa),所以00CAykxa，00CBykxa，直线AC的方程是00()yyaxaxa，与直线xm联立方程组得：00()xmyyxaxa，化简得：010()yamyxa，同理020()ymayxa，所以222012220()ymayyxa，又点C在椭圆上，所以有2200221xyab，2222002axayb，所以222122()bmayya，显然有2amc时，24222()MNbayyaac222(1)abc42bc（定值）6结论拓展在双曲线22221(0,0)xyabab中,点,AB是它的左右顶点,点C(不同于点,AB)是双曲线上的任意一点,连接直线,CACB,不难发现斜率之积CACBkk22ba(定值),如果直线,CACB与直线xm分别相交于点M,N,显然有2amc时，2421222()bayyaac42bc（定值）.这里不再熬诉.7统一结论结论1:过点(0,)a0a的直线交抛物线22(0)xpyp于点A、B，动直线AB及抛物线上动点C（不同于点A、B），设直线AC与直线BC相交直线ym分别于点M、N，存在一个ma,存在直线ya（仅与定点有关），使得2MNxxpa.结论2:在圆锥曲线(,)0fxy中,点,AB是它的左右顶点,点C(不同于点,AB)是圆锥曲线上的任意一点,连接直线,CACB,不难发现斜率之积CACBkk为定值,如果直线,CACB与直线xm分别相交于点M,N,存在2amc时，使得12yy42bc（定值）.8思考1、在全国各高校放开自主招生和三位一体招生的背景下，数学学业水平考试越来越受重视，数学老师重视对学科水平考试的试题尤其是定点线与圆锥曲线相交的有关问题的研究具有极大的现实意义。2、用类似科学研究的方法去解决问题的方式，提出结论，并进一步推理、论证解决问题，通过过定点直线与圆锥曲线相交结论相关性的分析，得出圆锥曲线中的统一结论。通过这种积极探究的方式，教师可以获得数学发现和创造的成功体验。3、对定点线与抛物线相交问题进一步探究，通过观察、类比、归纳，体现了数学的思考是自然的过程，对几个新的结论的推理、论证，有利于激发一线教师的教学热情，在“一题多解，一题多变，多题归一”的探究过程中领悟数学思想方法，把握数学本质。参考文献：1、马洪炎.运用焦半径公式速解焦点弦问题J.中学教研（数学）2013.72、蔡小雄,陈发志.云来山更佳云去山如画J.中学教研（数学）2013.103、朱贤良.莫让浮云遮望眼,除尽繁华识真颜----对一类高考试题本质的追溯J.中学数学教学参考:上旬,2013(6):1-3.4、林庆望.当偶然邂逅必然-----圆锥曲线的一个优美性质J.中学教研（数