3.1.2用二分法求方程的近似解2011.11.15

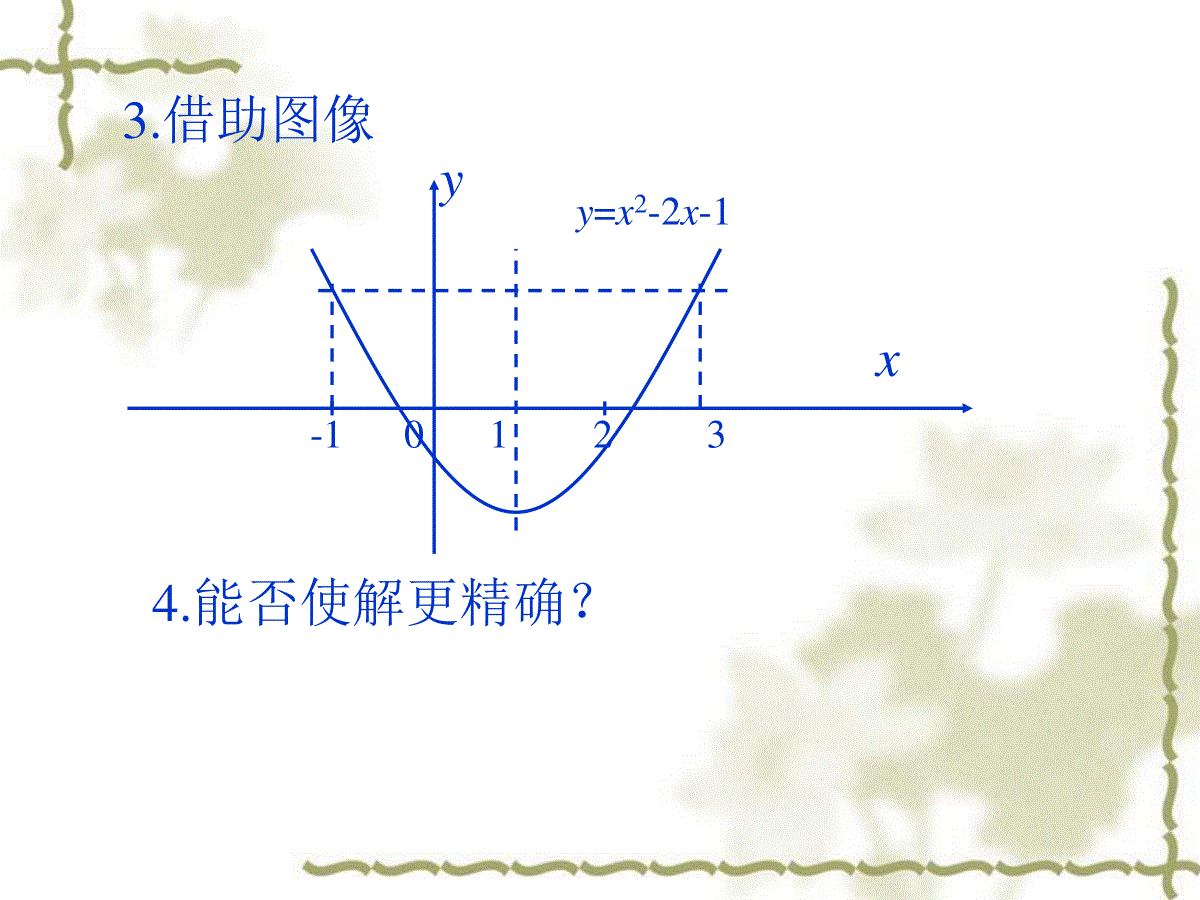
2020年4月22日星期三新疆王新敞特级教师源头学子小屋@[e-mail]源头学子小屋特级教师王新敞新疆；有六个乒乓球,已知其中五个球质量相同,只有一个球的质量偏重,而手边只有一架没有砝码的托盘天平.你能利用这架天平找出这个质量偏重的球吗?问题情境问题1:最少要称重几次才能找到这个质量偏重的乒乓球?答案:最少两次CCTV2“幸运52”片段：主持人李咏说道:猜一猜这架家用型数码相机的价格.观众甲:2000!李咏:高了!观众乙:1000!李咏:低了!观众丙:1500!李咏:还是低了!········问题2:你知道这件商品的价格在什么范围内吗?问题3:若接下来让你猜的话,你会猜多少价格比较合理呢?答案:1500至2000之间问题情境1.如何求方程的解：x2-2x-1=0提出问题：2.若不用求根公式能否求出近似解？12X=（x=2.4142或-0.4142）3.借助图像4.能否使解更精确？xyy=x2-2x-11203-123xy0y=x2-2x-12.52.3752.252.4375“取区间中点”区间[a，b]中点c=2ba分析：如何求方程x2-2x-1=0的一个正的近似解.（精确度0.05）方法探究-+23f(2)0，f(3)02x13-+22.53f(2)0，f(2.5)02x12.5-+22.252.53f(2.25)0，f(2.5)02.25x12.5-+22.3752.53f(2.375)0，f(2.5)02.375x12.5-+22.3752.43753f(2.375)0，f(2.4375)02.375x12.4375-+22.406252.43753f(2.40625)0，f(2.4375)02.40625x12.437540625.21xX=|2.4375-2.40625|=0.031250.05精确度ε:|a-b|εx1ε二分法定义：对于区间[a,b]上连续不断、且f(a)·f(b)0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法。2.用二分法求一元方程f(x)=0的近似解的基本步骤:1()2cab第一步确定初始区间[a,b]，验证f(a)f(b)0第二步求区间[a,b]两端点的平均值第三步计算f(c)并判断：(1)如果f(c)=0，则c就是f(x)的零点，计算终止;(2)如果f(a)f(c)0，则零点，否则零点。第四步重复步骤2～3,直至所得区间的两端点差的绝对值小于要求的精确值，则零点的近似值为所得区间内的任一数。),(cax),(bcx二分法的基本步骤一般取其中点为近似值。自行探究：例2.求函数f(x)=㏑x+2x-6的零点.(精确度为0.01）x12345f(x)-4-1.30691.09863.38635.6094yx123-0.10.10.2-0.20列表：（a，b)中点x1f(a)f(b)f(x1)求函数在区间（2，3）内的零点.(精确度0.01）()ln26fxxx2.531252.53906250.001781250.01ab2.53125所以函数的零点的近似值为：(2,3)-+2.5-0.084(2.5,3)-+2.750.512(2.5,2.75)-+0.215(2.5,2.625)-+2.6252.56250.066(2.5,2.5625)-+2.53125-0.009(2.53125,2.5625)-+2.5468750.029(2.53125,2.546875)-+2.53906250.010(2.53125,2.5390625)-+练习：1.下列函数图像与x轴均有交点，但不宜用二分法求交点横坐标的是()ABCDB练习2.函数f(x)=x3-2x2+3x-6在区间[-2,4]上的零点必定在()内其中f(1.75)0(A)[-2,1](B)[2.5,4](C)[1,1.75](D)[1.75,2.5]D例3.从上海到旧金山的海底电缆有15个接点，现在某接点发生故障，需及时修理，为了尽快断定故障发生点，一般至多需要检查接点的个数为几个？答：至多检查3个接点.二分法的应用练习1.用二分法求函数的零点,函数的零点总位于区间[an,bn]上,当时函数的近似零点与真正零点的误差不超过()A.mB.m/2C.2mD.m/4mbannBm取中点为近似零点真正的零点二分法的应用练习2.在一个风雨交加的夜里，从某水库闸房到防洪指挥部的电话线路发生了故障，这一条10km长的线路，如何迅速查出故障所在？要把故障可能发生的范围缩小到50～100m左右，即一两根电线杆附近，要检查多少次？算一算：答：7次答：用二分法第2次：10000÷22=2500第1次：10000÷2=5000第3次：10000÷23=1250第4次：10000÷24=625第5次：10000÷25=312.5第6次：10000÷26=156.25第7次：10000÷27=78.125二分法的应用小结1.二分法是求函数零点近似解的一种计算方法.2.用二分法求函数零点的一般步骤：（1）零点存在性定理,求出初始区间；（2）进行计算,确定下一区间（3）循环进行,达到精确要求⒊二分法渗透了极限和算法的思想.