当前位置:首页 > 中学教育 > 初中教育 > 分式及分式方程题型汇总
1分式单元复习(一)、分式定义及有关题型一、分式的概念:例:下列各式中,是分式的是①1+x1②)(21yx③3x④xm2⑤3xx⑥1394yx⑦x2、下列各式中,是分式的是①x1②)(21yx③3x④xm2⑤3xx⑥1394yx⑦y53、下列各式:xxxxyxxx2225,1,2,34,151其中分式共有()个。A、2B、3C、4D、5二、分式有意义的条件:分母不等于零例:当x时,分式22xx有意义;当x时,22x有意义。练习:1、当x时,分式6532xxx无意义。2.使分式||1xx无意义,x的取值是()A.0B.1C.1D.13、分式55xx,当______x时有意义。4、当a时,分式321aa有意义.5、当x时,分式22xx有意义。6、当x时,22x有意义。7、当x时,分式435xx的值为1;8.(辨析题)下列各式中,无论x取何值,分式都有意义的是()A.121xB.21xxC.231xxD.2221xx9当x为任意实数时,下列分式一定有意义的是()2A.23xB.212xC.1xD.211x三、分式的值为零说明:①分式的分子的值等于零;②分母不等于零例1:若分式242xx的值为0,那么x。例2.要使分式9632xxx的值为0,只须().(A)3x(B)3x(C)3x(D)以上答案都不对练习:1、当x时,分式6)2)(2(2xxxx的值为零。2、若分式242xx的值为0,那么x。3、如果分式2||55xxx的值为0,那么x的值是()4.分式12122aaa有意义的条件是,分式的值等于零的条件是。5.已知当2x时,分式axbx无意义,4x时,此分式的值为0,则ab的值等于()A.-6B.-2C.6D.26.使分式x312的值为正的条件是7.若分式9322aa的值为正数,求a的取值范围8、当x时,分式xx23的值为负数.9、若关于x的方程ax=3x-5有负数解,则a的取值范围是(二)分式的基本性质及有关题型分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变。1.填空:abyaxy;zyzyzyx2)(3)(6;3)0(1053aaxyxya1422aa222yxyx=yx.23xx=23xx;2:若A、B表示不等于0的整式,则下列各式成立的是().(A)MBMABA(M为整式)(B)MBMABA(M为整式)(C)22BABA(D))1()1(22xBxABA3、下列各式中,正确的是()A.amabmbB.abab=0C.1111abbaccD.221xyxyxy题型一:化分数系数、小数系数为整数系数【例1】不改变分式的值,把分子、分母的系数化为整数.(1)yxyx41313221(2)baba04.003.02.0练习:1.不改变分式的值,把下列分式的分子、分母的系数化为整数.(1)yxyx5.008.02.003.0(2)baba10141534.0题型二:分式的符号变化:【例2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.(1)yxyx(2)baa(3)ba1、不改变分式的值,使下列分式的分子与分母的最高次项的系数是正数。①13232aaaa=②32211xxxx=③1123aaa=2.(探究题)下列等式:①()ababcc;②xyxyxx;③ababcc;④mnmnmm中,成立的是()A.①②B.③④C.①③D.②④题型三:分式的倍数变化:41、如果把分式yxx232中的x,y都扩大3倍,那么分式的值2、.如果把分式63xxy中的x,y都扩大10倍,那么分式的值3、把分式22xyxy中的x,y都扩大2倍,则分式的值()A.不变B.扩大2倍C.扩大4倍D.缩小2倍4、把分式2aba中的a、b都扩大2倍,则分式的值(C).(A)扩大2倍(B)扩大4倍(C)缩小2倍(D)不变.7、若把分式xyyx2中的x和y都扩大3倍,那么分式的值()A、扩大3倍B、不变C、缩小3倍D、缩小6倍2、若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是()A、yx23B、223yxC、yx232D、2323yx(三)分式的运算一、分式的约分:1、约分(1)2912xxy(2)abba22(3)96922xxx(4)ababa2222.计算:)3(3234422aaaaaa3.计算:2222223223yxyxyxyxyxyx.4、化简2293mmm的结果是()A、3mmB、3mmC、3mmD、mm355.分式434yxa,2411xx,22xxyyxy,2222aababb中是最简分式的有()A.1个B.2个C.3个D.4个6、下列公式中是最简分式的是()A.21227baB.22()abbaC.22xyxyD.22xyxy二、最简公分母1.在解分式方程:412xx+2=xx212的过程中,去分母时,需方程两边都乘以最简公分母是___________________.2、分式,21xxyy51,212的最简公分母为。3.计算:1123xxxx.三.分式的计算:1、xyyyxx2222、112aaa3计算:(1)42232)()()(abcabccba;(2)22233)()()3(xyxyyxyxa;(3)mnmnmnmnnm22;(4)112aaa;4化简分式(﹣)÷,并从﹣1≤x≤3中选一个你认为合适的整数x代入求值.5、222222yxyxyyxyxyx,其中0|3|)2(2yx66、baaba27、)1(111112xxx8、111122aaaaaa9、225262xxxx10、4222xxxxxx四.求待定字母的值1.若111312xNxMxx,试求NM,的值.2.若已知132112xxxBxA(其中A、B为常数),则A=__________,B=__________;3.已知:21xx,求221xx的值.4.若0)32(|1|2xyx,求yx241的值.5.已知411ba,求分式babababa222的值。6.已知13xy,求5352xxyyxxyy的值.77、已知a2-3a+1=0,则221aa=____________8、已知bbaaNbaMab11,1111,1,则M与N的关系为()A.MNB.M=NC.MND.不能确定.9、若4x=5y,则222yyx的值等于()A41B51C169D25910、已知nmnm111,则nmmn。(一)分式方程题型分析题型一:用常规方法解分式方程【例1】解下列分式方程(1)xx311;(2)0132xx;(2)(3)114112xxx;(4)xxxx4535题型二:求待定字母的值1.若关于x的分式方程3132xmx有增根,求m的值.2.若分式方程122xax的解是正数,求a的取值范围.3.已知关于x的方程322xmx的解是正数,则m的取值范围为.4.若1044mxxx无解,则m的值是()8A.—2B.2C.3D.—35.在一段坡路,小明骑自行车上坡的速度为每小时v1千米,下坡时的速度为每小时v2千米,则他在这段路上、下坡的平均速度是每小时()A.千米B.千米C.千米D.无法确定6.一辆汽车往返于相距akm的甲、乙两地,去时每小时行mkm,返回时每小时行nkm,则往返一次所用的时间是_____________.7.甲打字员打9000个字所用的时间与乙打字员打7200个字所用的时间相同,已知甲、乙两人每小时共打5400个字,问甲、乙两个打字员每小时各打多少个字?8.一名同学计划步行30千米参观博物馆,因情况变化改骑自行车,且骑车的速度是步行速度的1.5倍,才能按要求提前2小时到达,求这位同学骑自行车的速度。9.从甲地到乙地的路程是15千米,A骑自行车从甲地到乙地先走,40分钟后,B乘车从甲地出发,结果同时到达。已知B乘车速度是A骑车速度的3倍,求两车的速度。10.小张和小王同时从学校出发去距离15千米的一书店买书,小张比小王每小时多走1千米,结果比小王早到半小时,设小王每小时走x千米,则可列出的的方程是()A、2115115xxB、2111515xxC、2115115xxD、2111515xx11、赵强同学借了一本书,共280页,要在两周借期内读完,当他读了一半时,发现平时9每天要多读21页才能在借期内读完.他读了前一半时,平均每天读多少页?如果设读前一半时,平均每天读x页,则下列方程中,正确的是()A、1421140140xxB、1421280280xxB、1211010xxD、1421140140xx12、某校师生到距学校20千米的公路旁植树,甲班师生骑自行车先走45分钟后,乙班的师生乘汽车出发,结果两班师生同时到达.已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?13、怀化市某乡积极响应党中央提出的“建设社会主义新农村”的号召,在本乡建起了农民文化活动室,现要将其装修.若甲、乙两个装修公司合做需8天完成,需工钱8000元;若甲公司单独做6天后,剩下的由乙公司来做,还需12天完成,共需工钱7500元.若只选一个公司单独完成.从节约开始角度考虑,该乡是选甲公司还是选乙公司?请你说明理由.14、在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成.(1)求乙工程队单独完成这项工程所需的天数;(2)求两队合做完成这项工程所需的天数.
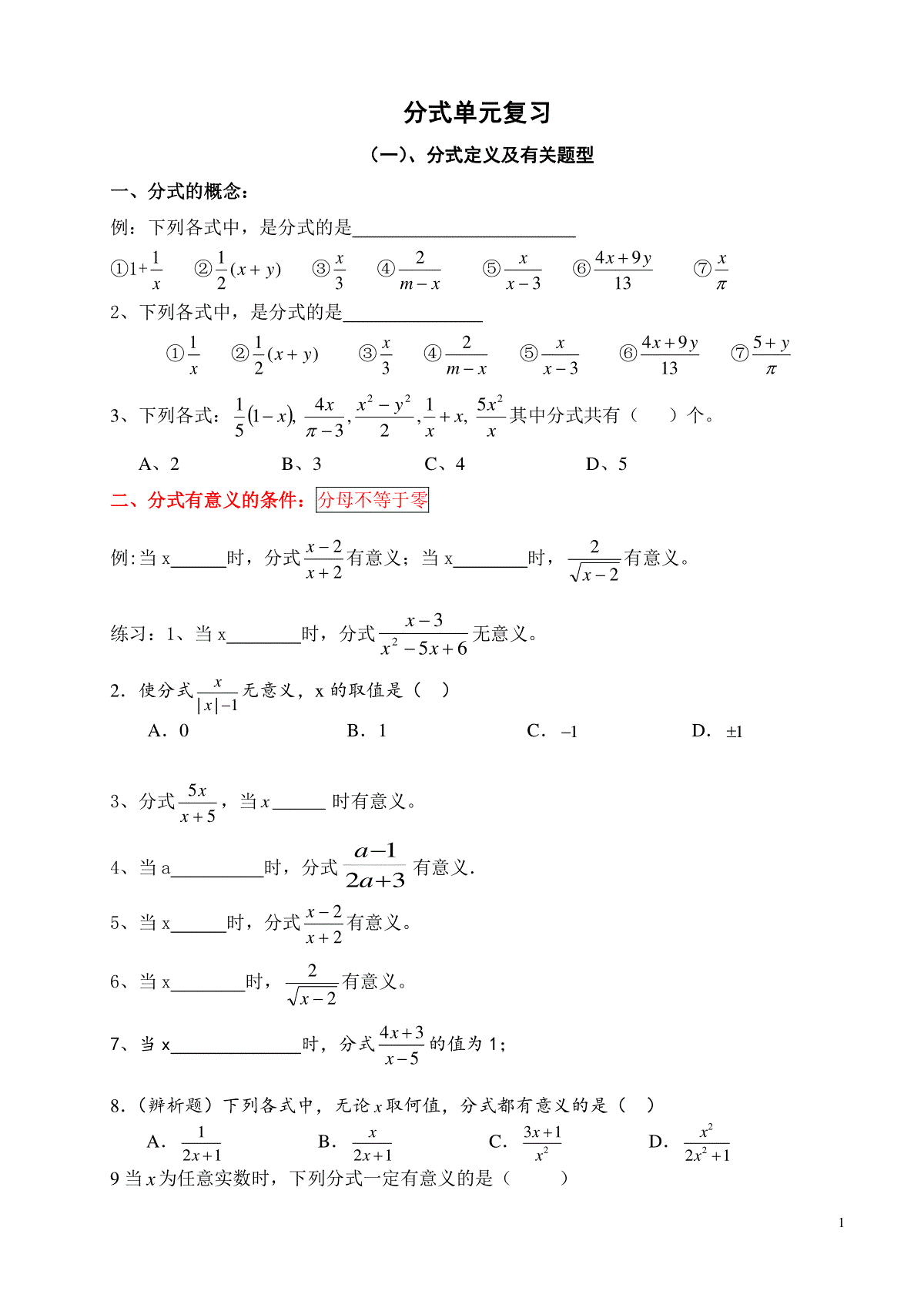



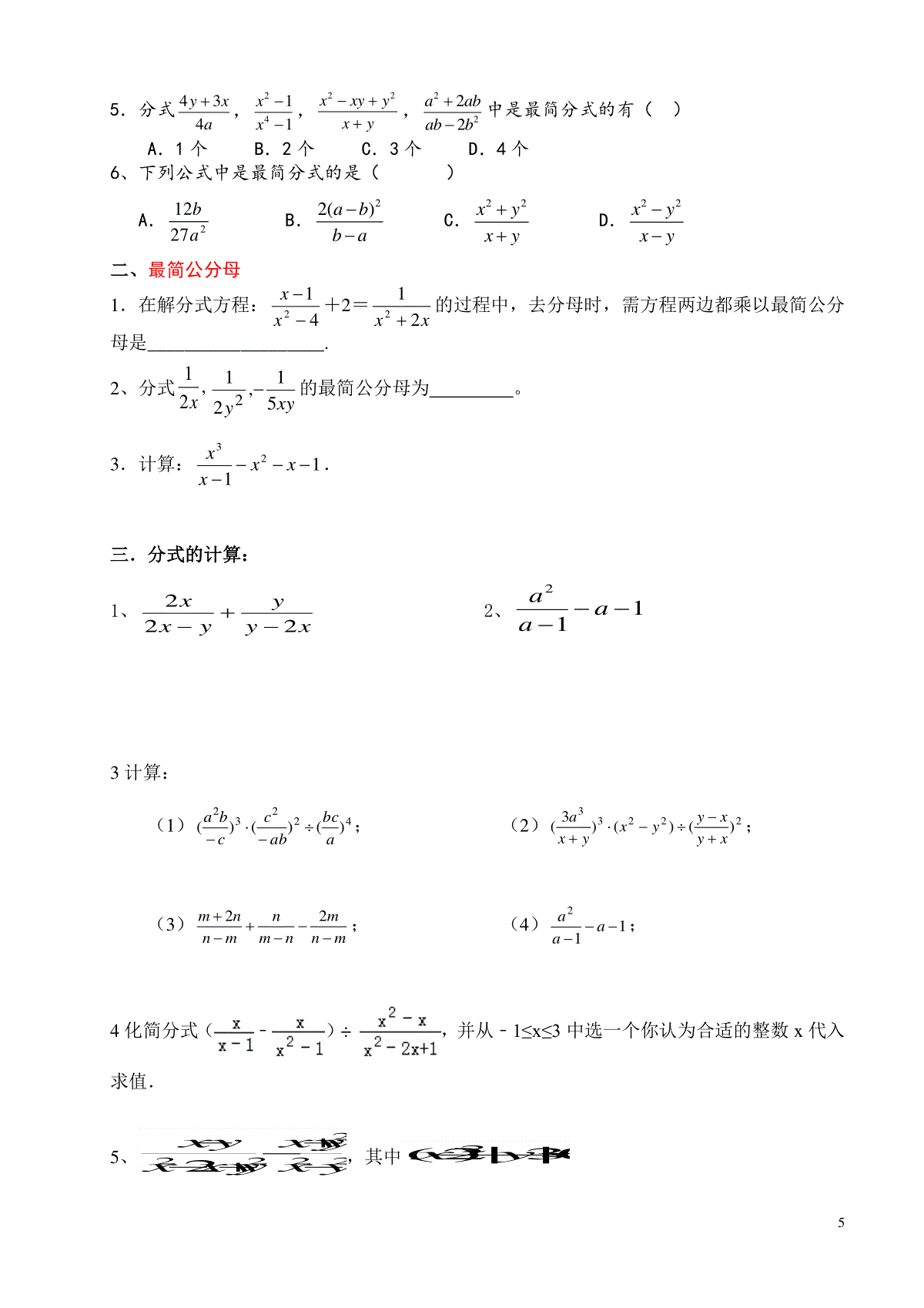
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:分式及分式方程题型汇总
链接地址:https://www.777doc.com/doc-5403623 .html