单纯形法例题

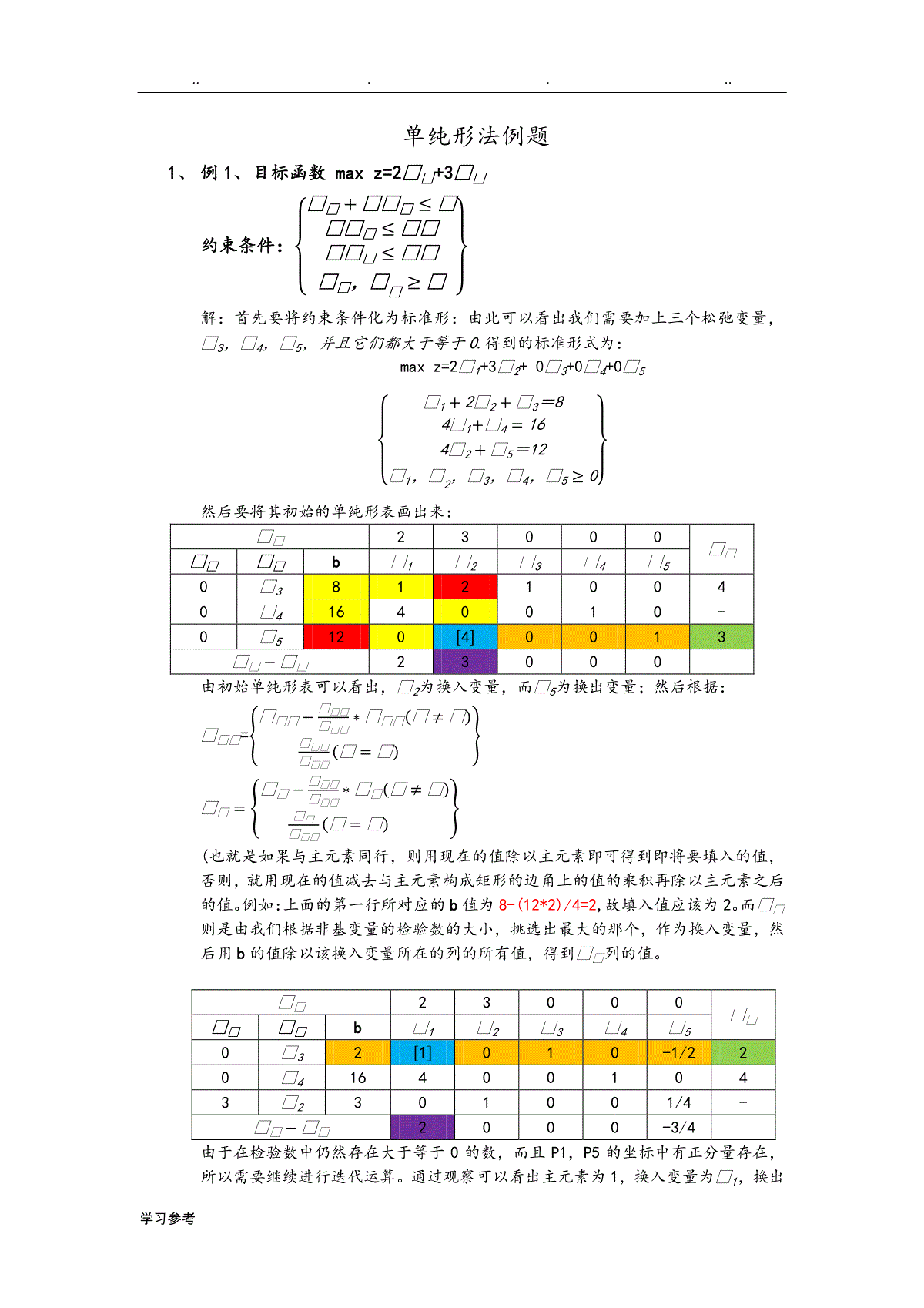
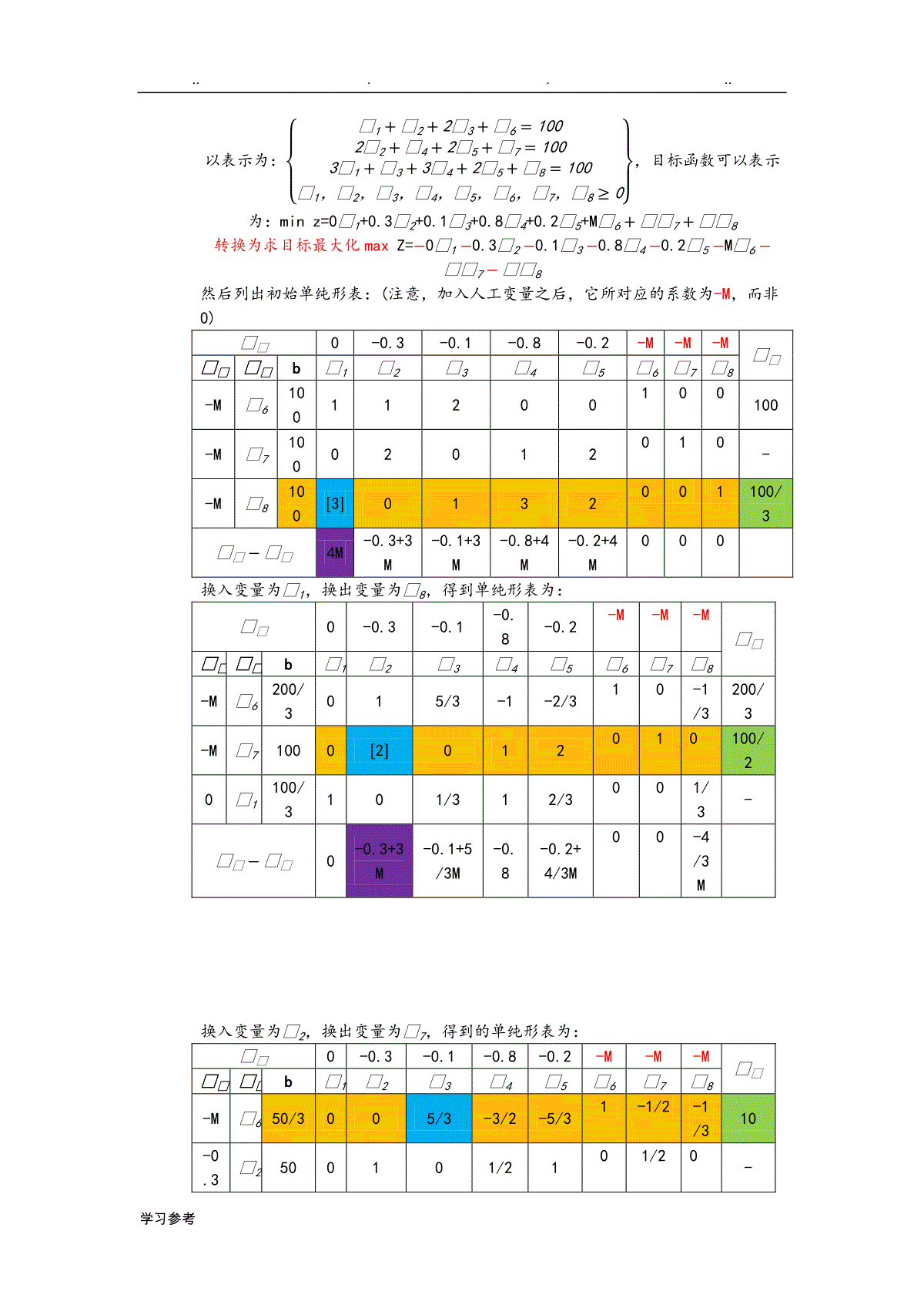
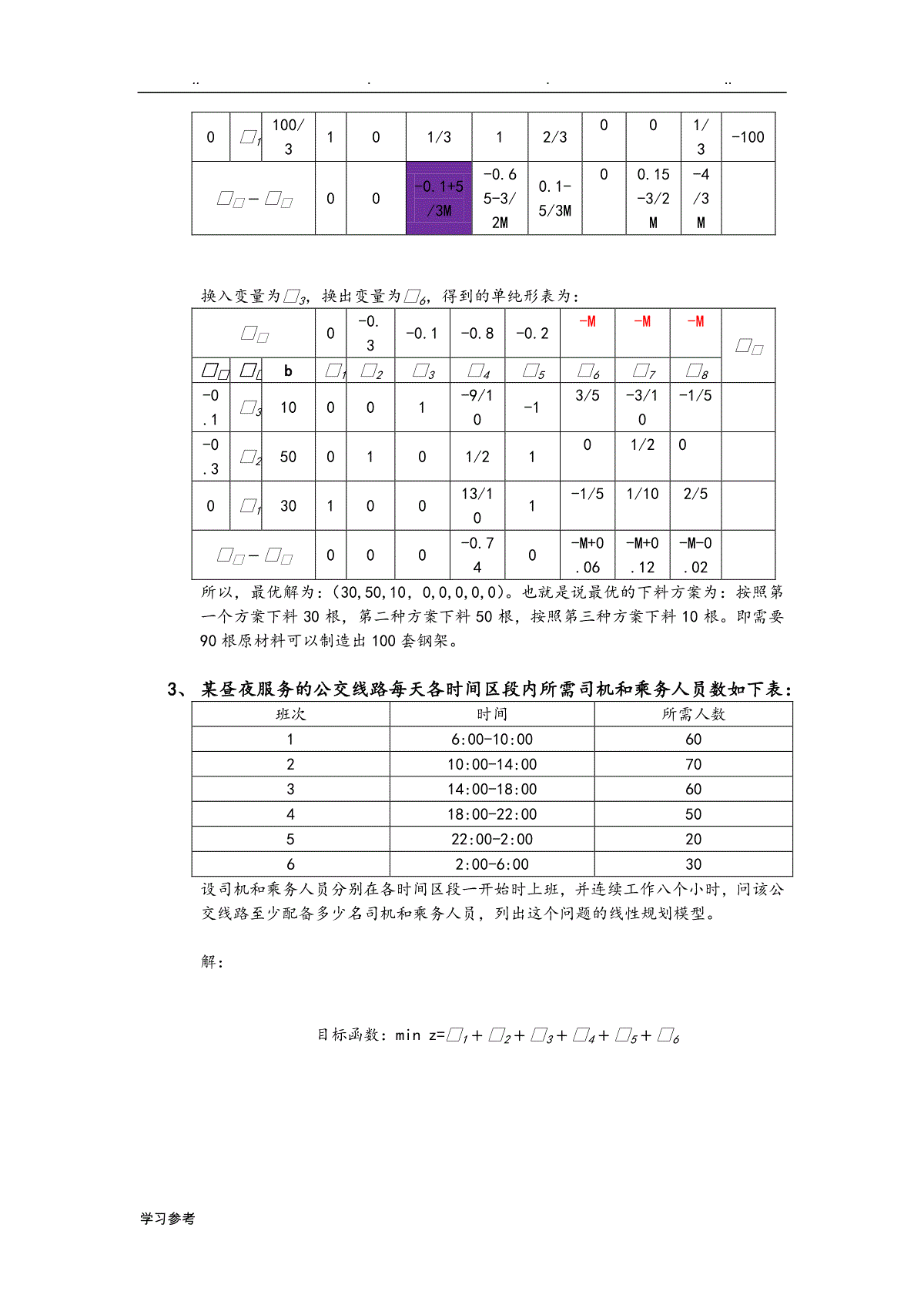
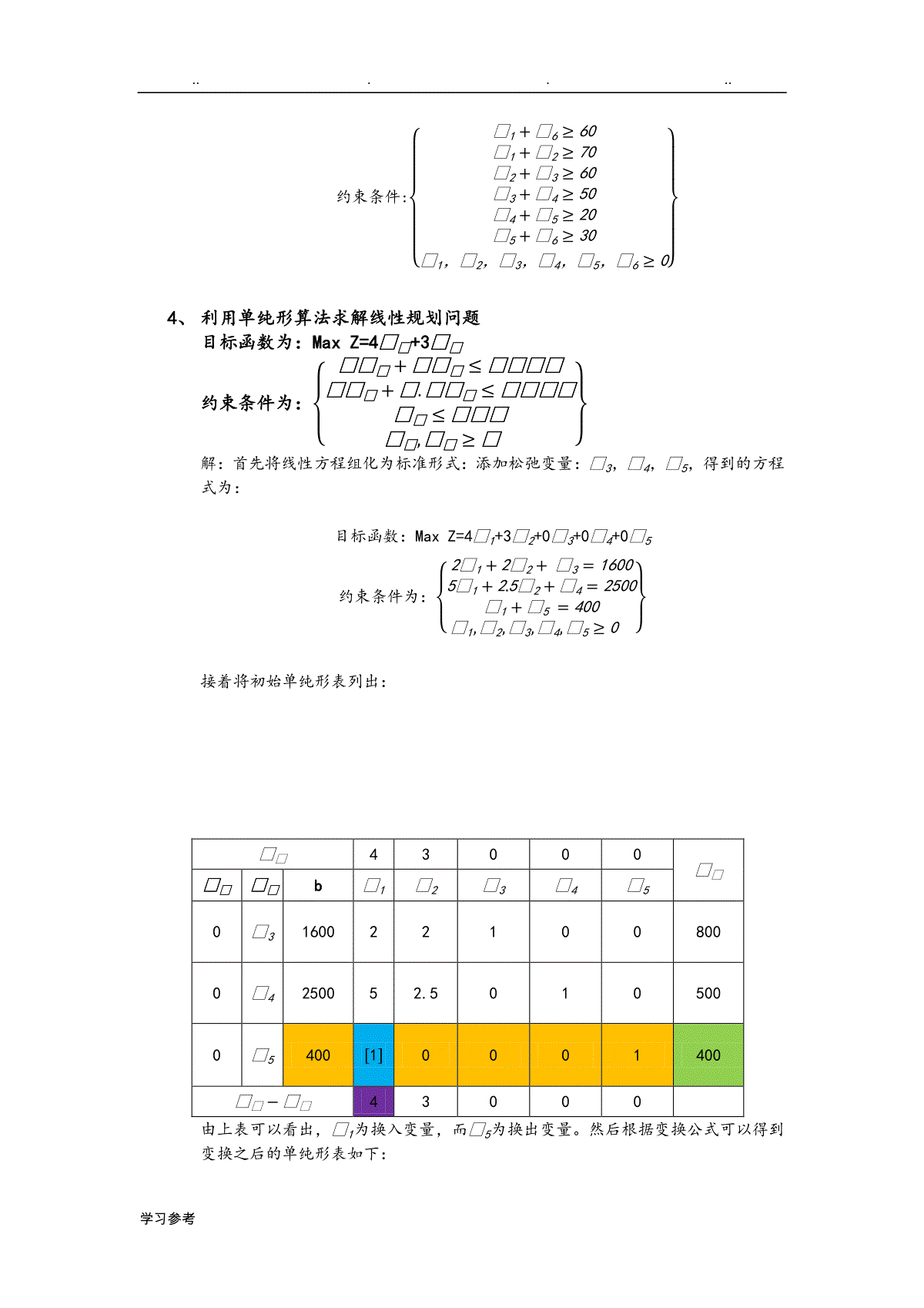
......学习参考单纯形法例题1、例1、目标函数maxz=2𝒙𝒙+3𝒙𝒙约束条件：{𝒙𝒙+𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙，𝒙𝒙≥𝒙}解：首先要将约束条件化为标准形：由此可以看出我们需要加上三个松弛变量，𝒙3，𝒙4，𝒙5，并且它们都大于等于0.得到的标准形式为：maxz=2𝒙1+3𝒙2+0𝒙3+0𝒙4+0𝒙5{𝒙1+2𝒙2+𝒙3＝84𝒙1+𝒙4=164𝒙2+𝒙5＝12𝒙1，𝒙2，𝒙3，𝒙4，𝒙5≥0}然后要将其初始的单纯形表画出来：𝒙𝒙23000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙381210040𝒙41640010-0𝒙5120[4]0013𝒙𝒙−𝒙𝒙23000由初始单纯形表可以看出，𝒙2为换入变量，而𝒙5为换出变量；然后根据：𝒙𝒙𝒙={𝒙𝒙𝒙−𝒙𝒙𝒙𝒙𝒙𝒙∗𝒙𝒙𝒙(𝒙≠𝒙)𝒙𝒙𝒙𝒙𝒙𝒙(𝒙=𝒙)}𝒙𝒙={𝒙𝒙−𝒙𝒙𝒙𝒙𝒙𝒙∗𝒙𝒙(𝒙≠𝒙)𝒙𝒙𝒙𝒙𝒙(𝒙=𝒙)}(也就是如果与主元素同行，则用现在的值除以主元素即可得到即将要填入的值，否则，就用现在的值减去与主元素构成矩形的边角上的值的乘积再除以主元素之后的值。例如：上面的第一行所对应的b值为8-(12*2)/4=2,故填入值应该为2。而𝒙𝒙则是由我们根据非基变量的检验数的大小，挑选出最大的那个，作为换入变量，然后用b的值除以该换入变量所在的列的所有值，得到𝒙𝒙列的值。𝒙𝒙23000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙32[1]010-1/220𝒙4164001043𝒙2301001/4-𝒙𝒙−𝒙𝒙2000-3/4由于在检验数中仍然存在大于等于0的数，而且P1，P5的坐标中有正分量存在，所以需要继续进行迭代运算。通过观察可以看出主元素为1，换入变量为𝒙1，换出......学习参考变量为𝒙3，故得到的单纯形表如下：𝒙𝒙23000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙52𝒙121010-1/2-0𝒙4800-41[2]43𝒙2301001/412𝒙𝒙−𝒙𝒙00-201/4由于检验数中存在正数，且P5和P3中有正分量存在，所以需要继续迭代(换入变量为𝒙5，换出变量为𝒙4：得到单纯形表如下：𝒙𝒙23000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙52𝒙141001/400𝒙5400-21/213𝒙22011/2-1/80𝒙𝒙−𝒙𝒙00-3/2-1/80此时可以发现检验数中没有大于0的数，表明已经得到了最优解，所以最优解是：（4,2,0,0,4），故目标函数值z=2*4+2*3=142、合理利用线材问题，现在要做100套钢架，每套用长为2.9m，2.1m，和1.5m的钢各一根，已知原料长7.4m，问应如何下料，使用的原材料最省；解：首先我们必须要清楚该问题的需要设立的变量是什么。我们分析一下问题，做100套钢架，需要2.9m长的钢100根，2.1m的钢100根，1.5m的钢100根。而一份原料长度是7.4m，它的截取的方法有多少种，我们可以用表格列举出来：长度/m下料根数截取方案123452.91122.12121.53132所用长度7.47.17.36.67.2剩余长度00.30.10.80.2求解的问题是关于如何去进行下料，使得原材料最省，也就是说如何搭配使用这些方案，使得剩余的总长度最少。由此，我们可以将目标函数和约束条件表述出来：目标函数：minz=0.3𝒙2+0.1𝒙3+0.8𝒙4+0.2𝒙5约束条件{𝒙1+𝒙2+2𝒙3=1002𝒙2+𝒙4+2𝒙5=1003𝒙1+𝒙3+3𝒙4+2𝒙5=100𝒙1，𝒙2，𝒙3，𝒙4，𝒙5≥0}首先可以写出线性方程组的矩阵形式：[112000201230132]发现不存在单位矩阵，所以要采用人造基的方式，也就是要添加人工变量：𝒙6，𝒙7，𝒙8，那么线性方程组可......学习参考以表示为：{𝒙1+𝒙2+2𝒙3+𝒙6=1002𝒙2+𝒙4+2𝒙5+𝒙7=1003𝒙1+𝒙3+3𝒙4+2𝒙5+𝒙8=100𝒙1，𝒙2，𝒙3，𝒙4，𝒙5，𝒙6，𝒙7，𝒙8≥0}，目标函数可以表示为：minz=0𝒙1+0.3𝒙2+0.1𝒙3+0.8𝒙4+0.2𝒙5+M𝒙6+𝒙𝒙7+𝒙𝒙8转换为求目标最大化maxZ=−0𝒙1−0.3𝒙2−0.1𝒙3−0.8𝒙4−0.2𝒙5−M𝒙6−𝒙𝒙7−𝒙𝒙8然后列出初始单纯形表：(注意，加入人工变量之后，它所对应的系数为-M，而非0)𝒙𝒙0-0.3-0.1-0.8-0.2-M-M-M𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙5𝒙6𝒙7𝒙8-M𝒙610011200100100-M𝒙710002012010--M𝒙8100[3]0132001100/3𝒙𝒙−𝒙𝒙4M-0.3+3M-0.1+3M-0.8+4M-0.2+4M000换入变量为𝒙1，换出变量为𝒙8，得到单纯形表为：𝒙𝒙0-0.3-0.1-0.8-0.2-M-M-M𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙5𝒙6𝒙7𝒙8-M𝒙6200/3015/3-1-2/310-1/3200/3-M𝒙71000[2]012010100/20𝒙1100/3101/312/3001/3-𝒙𝒙−𝒙𝒙0-0.3+3M-0.1+5/3M-0.8-0.2+4/3M00-4/3M换入变量为𝒙2，换出变量为𝒙7，得到的单纯形表为：𝒙𝒙0-0.3-0.1-0.8-0.2-M-M-M𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙5𝒙6𝒙7𝒙8-M𝒙650/3005/3-3/2-5/31-1/2-1/310-0.3𝒙2500101/2101/20-......学习参考0𝒙1100/3101/312/3001/3-100𝒙𝒙−𝒙𝒙00-0.1+5/3M-0.65-3/2M0.1-5/3M00.15-3/2M-4/3M换入变量为𝒙3，换出变量为𝒙6，得到的单纯形表为：𝒙𝒙0-0.3-0.1-0.8-0.2-M-M-M𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙5𝒙6𝒙7𝒙8-0.1𝒙310001-9/10-13/5-3/10-1/5-0.3𝒙2500101/2101/200𝒙13010013/101-1/51/102/5𝒙𝒙−𝒙𝒙000-0.740-M+0.06-M+0.12-M-0.02所以，最优解为：（30,50,10，0,0,0,0,0）。也就是说最优的下料方案为：按照第一个方案下料30根，第二种方案下料50根，按照第三种方案下料10根。即需要90根原材料可以制造出100套钢架。3、某昼夜服务的公交线路每天各时间区段内所需司机和乘务人员数如下表：班次时间所需人数16:00-10:0060210:00-14:0070314:00-18:0060418:00-22:0050522:00-2:002062:00-6:0030设司机和乘务人员分别在各时间区段一开始时上班，并连续工作八个小时，问该公交线路至少配备多少名司机和乘务人员，列出这个问题的线性规划模型。解：目标函数：minz=𝒙1+𝒙2+𝒙3+𝒙4+𝒙5+𝒙6......学习参考约束条件:{𝒙1+𝒙6≥60𝒙1+𝒙2≥70𝒙2+𝒙3≥60𝒙3+𝒙4≥50𝒙4+𝒙5≥20𝒙5+𝒙6≥30𝒙1，𝒙2，𝒙3，𝒙4，𝒙5，𝒙6≥0}4、利用单纯形算法求解线性规划问题目标函数为：MaxZ=4𝒙𝒙+3𝒙𝒙约束条件为：{𝒙𝒙𝒙+𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙𝒙𝒙𝒙+𝒙.𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙𝒙𝒙≤𝒙𝒙𝒙𝒙𝒙,𝒙𝒙≥𝒙}解：首先将线性方程组化为标准形式：添加松弛变量：𝒙3，𝒙4，𝒙5，得到的方程式为：目标函数：MaxZ=4𝒙1+3𝒙2+0𝒙3+0𝒙4+0𝒙5约束条件为：{2𝒙1+2𝒙2+𝒙3=16005𝒙1+2.5𝒙2+𝒙4=2500𝒙1+𝒙5=400𝒙1,𝒙2,𝒙3,𝒙4,𝒙5≥0}接着将初始单纯形表列出：𝒙𝒙43000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙31600221008000𝒙4250052.50105000𝒙5400[1]0001400𝒙𝒙−𝒙𝒙43000由上表可以看出，𝒙1为换入变量，而𝒙5为换出变量。然后根据变换公式可以得到变换之后的单纯形表如下：......学习参考𝒙𝒙43000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙38000210-24000𝒙45000[2.5]01-52004𝒙1400100010𝒙𝒙−𝒙𝒙0300-4由上表可以看出，换入变量为𝒙2，换出变量为𝒙4，单纯形表如下：𝒙𝒙43000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙3400001-4/5[2]2003𝒙22000102/5-2-4𝒙140010001400𝒙𝒙−𝒙𝒙000-6/52由上表可以看出，换入变量为𝒙5，换出变量为𝒙3得到的单纯形表如下：𝒙𝒙43000𝒙𝒙𝒙𝒙𝒙𝒙b𝒙1𝒙2𝒙3𝒙4𝒙50𝒙5200001/2-2/513𝒙2600011-2/504𝒙12001002/50𝒙𝒙−𝒙𝒙00-3-2/50由于，检验数均为非负，所以得到了最优解，且最优解为(200,600,0,0,200);......学习参考故目标函数的最大值为：Z=26001.若不给自己设限，则人生中就没有限制你发挥的藩篱。2.若不是心宽似海，哪有人生风平浪静。在纷杂的尘世里，为自己留下一片纯静的心灵空间，不管是潮起潮落，也不管是阴晴圆缺，你都可以免去浮躁，义无反顾，勇往直前，轻松自如地走好人生路上的每一步3.花一些时间，总会看清一些事。用一些事情，总会看清一些人。有时候觉得自己像个神经病。既纠结了自己，又打扰了别人。努力过后，才知道许多事情，坚持坚持，就过来了。4.岁月是无情的，假如你丢给它的是一片空白，它还给你的也是一片空白。岁月是有情的，假如你奉献给她的是一些色彩，它奉献给你的也是一些色彩。你必须努力，当有一天蓦然回首时，你的回忆里才会多一些色彩斑斓，少一些苍白无力。只有你自己才能把岁月描画成一幅难以忘怀的人生画卷。