第一章气体的PVT性质.

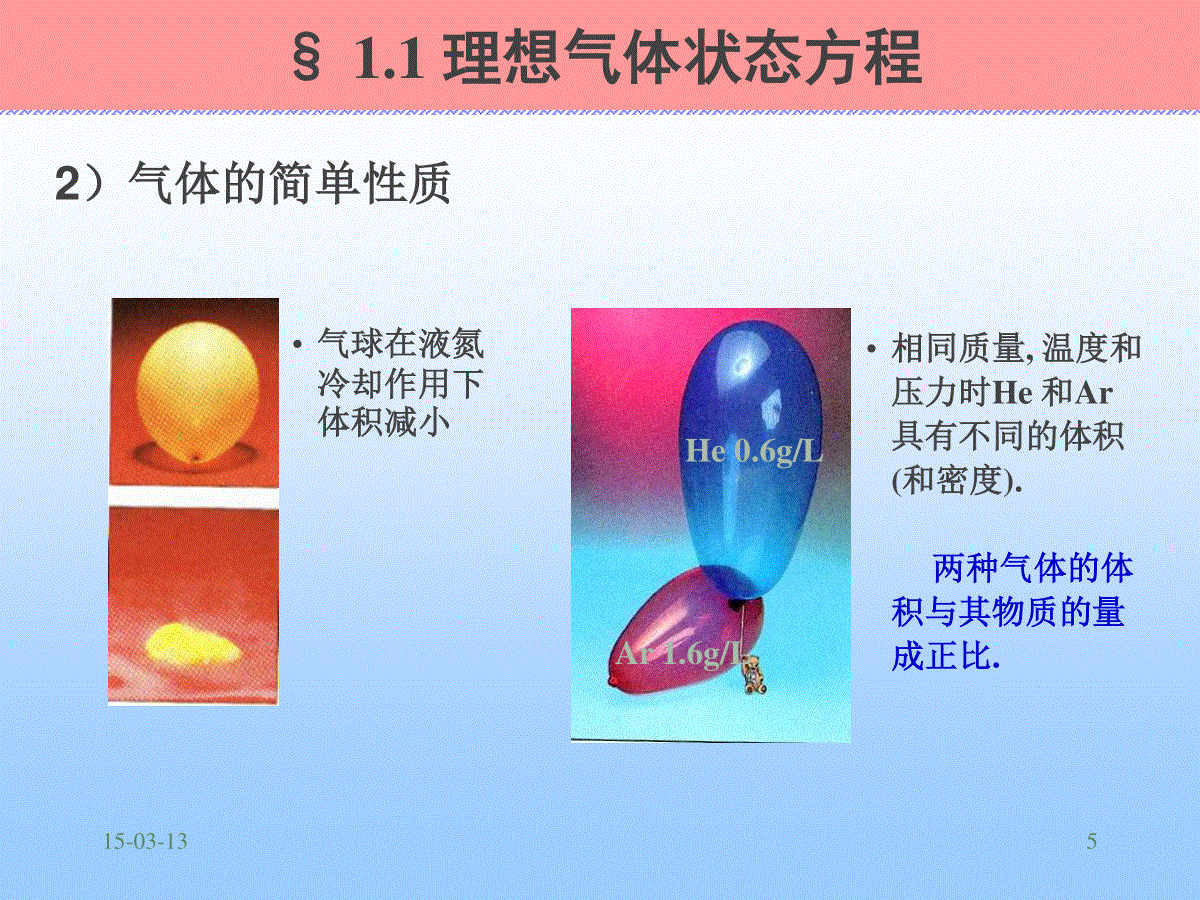
15-03-13115-03-132•热气球第一章气体的pVT性质15-03-133第一章气体的pVT性质§1.1理想气体状态方程§1.2道尔顿分压定律与阿玛格分体积定律§1.3真实气体的状态方程§1.4气体的液化15-03-134§1.1理想气体状态方程1.物质的聚集状态物质的聚集状态气体gV受T、p的影响很大液体l固体sV受T、p的影响较小（又称凝聚态）气体分子间作用力较液、固体小得多，所以气体的性质相对液、固体简单得多，人们对气体研究比较完美,比较方便。利用气体的一些性质，并加以修正，可处理液、固体行为，所得结果能令人满意。1）15-03-135§1.1理想气体状态方程•气球在液氮冷却作用下体积减小•相同质量,温度和压力时He和Ar具有不同的体积(和密度).两种气体的体积与其物质的量成正比.He0.6g/LAr1.6g/L2）气体的简单性质15-03-136§1.1理想气体状态方程气体纯气体混合气体压力温度体积n压力温度体积组成描述气体状态的量15-03-137§1.1理想气体状态方程2.压力、体积、温度1）压力单位面积器壁上所受的力pP法定计量单位Pa2）体积气体所占空间的大小Vm3气体的体积是气体容器的体积15-03-138§1.1理想气体状态方程3）温度定量反映物体冷热程度的物理量摄氏温度t℃热力学温度TKT/K=t/℃+273.15绝对零度：在此温度下，构成物质的所有分子和原子均停止运动。-273.15K15-03-139§1.1理想气体状态方程联系p、V、T之间关系的方程称为状态方程本章中主要讨论气体的状态方程气体的讨论理想气体实际气体在气液固三种聚集状态中,气体最容易用分子模型进行研究.15-03-1310•在物质的众多宏观性质中,p,V,T三者意义明确,易于测量.下列函数关系称为状态方程:f(p,V,T,n)=0气体具有易压缩性,体积受压力和温度的影响很大.•气体分子的无规则运动NH3(g)和HCl(g)在空中化合成NH4Cl(s)•高氯酸铵分解放出大量气体,用于作火箭推进剂§1.1理想气体状态方程15-03-1311•AmedeoAvogadro(1776—1856)anItalian•RobertBoyle(1627—1691)BorninIreland•JosephGay-Lussac(1778—1850)Frenchman气体理论的三位奠基者:§1.1理想气体状态方程盖吕萨克波义尔阿伏加德罗15-03-1312波义尔定律pV=常数(n,T恒定)盖吕萨克定律V/T=常数(n,p恒定)阿伏加德罗定律V/n=常数(T,p恒定)§1.1理想气体状态方程3.理想气体状态方程:上述三经验定律相结合,得到pV=nRT式中R为摩尔气体常数,数值为8.314，单位Jmol-1K-1.与气体种类无关单位：pPaVm3TKnmol15-03-1313•烧杯里的铅的重量增加,针管里的气体体积减小•随着烧瓶里的气体被抽出,药用蜀葵内含的气体体积膨胀•玻义尔J管§1.1理想气体状态方程pV=常数15-03-1314•波义耳定律的一个应用——气压水井pV=常数15-03-1315§1.1理想气体状态方程气体压力越低就越符合这个关系式。4.理想气体状态方程的表达形式1）pV=nRT2）pVm=RT3）pV=(m/M)RT4）pM=RT（1-1）（1-2）（1-3）（1-4）Vm=V/n摩尔体积m3mol-115-03-1316§1.1理想气体状态方程例题某厂氢气柜的设计容积为2.00×103m3,设计容许压力为5.00×103kPa。设氢气为理想气体，问气柜在298.15K时最多可装多少氢气？解由已知有V=2.00×103m3,p=5.00×103kPa，T=298.15Kmn=pV/(RT)n=4.034×106molM——H2的摩尔质量=2.016×10-3kgmol-115-03-1317例：用管道输送天然气，当输送压力为200kPa，温度为25oC时，管道内天然气的密度为多少？假设天然气可看作是纯的甲烷。3333mkg1.294mkg273.15)(258.3151016.0410200RTpMVmρ解：M甲烷＝16.04×10－3kg·mol-1§1.1理想气体状态方程15-03-1318理想气体:凡在任何温度、压力下均服从理想气体状态方程的气体称为理想气体.理想气体的两个特征:(1)分子本身必定不占有体积;(2)分子间无相互作用.解释:(1)T恒定时,pVm=常数,意味着p,Vm0.(2)p=(n/V)RT,表明在恒温下,气体分子碰撞器壁的压力与分子数密度成简单的比例关系,而这只有在分子间没有相互作用时才有可能.理想气体模型分子是质点15-03-1319理想气体模型理想气体是一个理想的模型客观上不存在P趋于0理想气体状态方程近似适用于低压实际气体.易液化气体的适用压力范围较窄,难液化气体则相对较宽.15-03-13201.混合物的组成1)摩尔分数x或yxB(或yB)defnB/nB（单位为1）显然xB=1,yB=1本书中气体混合物的摩尔分数一般用y表示液体混合物的摩尔分数一般用x表示2)质量分数wBwBdefmB/mB（单位为1）mB=1§1.2道尔顿分压定律与阿玛格分体积定律15-03-1321§1.2理想气体混合物的分压定律与分体积定律若构成混合气体的各种气体均是理想气体，而且混合气体仍服从理想气体状态方程，则此混合气体称为理想气体混合物。15-03-1322BBpyp§1.2理想气体混合物的分压定律与分体积定律2.道尔顿分压定律1）分压力对于任何气体混合物，分压为BBpp普遍适用15-03-1323§1.2理想气体混合物的分压定律与分体积定律VnRTp/VRTnpypByBB2）道尔顿分压定律对于理想气体混合物物质的量为nB的理想气体B在温度为T、体积为V时所具有的压力。VRTnpBB/理想气体混合物中某一组分B的分压pB等于该组分单独存在于混合气体的T、V时产生的压力。15-03-1324§1.2理想气体混合物的分压定律与分体积定律BBpp理想气体的总压力等于混合气体中各组分气体在与混合气体具有相同的T、V条件下单独存在时所产生的压力之和。道尔顿分压定律低压下的真实气体VRTnpBB15-03-1325§1.2理想气体混合物的分压定律与分体积定律VRTnp总总VRTnpAAVRTnP总总15-03-1326§1.2理想气体混合物的分压定律与分体积定律例1molN2和3molH2混合，在298.15K时，体积为4.00m3。求混合气体的总压力和各组分气体的分压力。（设混合气体为理想气体混合物）某烃类混合气体的压力为100KPa，其中水蒸气的分压力为20KPa，求每100mol该混合气体中所含水蒸气的质量15-03-1327§1.2理想气体混合物的分压定律与分体积定律VyVBB3.阿马格分体积定律1)分体积:混合气体的任一组分的分体积是该组分单独存在于混合气体的温度、压力条件下占有的体积.对混合气体BBVV15-03-1328§1.2理想气体混合物的分压定律与分体积定律pRTnyVyVBBBpRTnVBB2）阿玛格分体积定律物质的量为nB的理想气体B在温度为T压力为p时所具有的体积理想混合气体的总体积等于理想混合气体中各组分气体在与理想混合气体具有相同温度和相同压力条件下单独存在时所占有的体积之和低压下的真实气体pRTnV15-03-1329§1.2理想气体混合物的分压定律与分体积定律3)体积分数混合气体中某组分i的分体积与总体积之比称该组分i的体积分数。iiiiynnPnRTPRTnVV//即体积分数等于该组分i的摩尔分数此规律只近似应用于低压下的实际混合气体。15-03-1330对于理想气体：nnV/nRTV/RTnPPyiiiinnP/nRTP/RTnVVyiiii体积分数等于压力分数等于该组分i的摩尔分数§1.2理想气体混合物的分压定律与分体积定律15-03-1331§1.2理想气体混合物的分压定律与分体积定律例某种只含有CO2一个酸性组分的混合气体，于室温常压下取样100.00mL。经过NaOH溶液充分洗涤后，在同样的温度及压力条件下，测得剩余气体的体积为90.50mL。求混合气体中CO2的摩尔分数。（设混合气体为理想气体混合物）15-03-1332§1.2理想气体混合物的分压定律与分体积定律4.气体混合物的平均摩尔质量因理想气体分子间没有相互作用，分子本身又不占体积，所以理想气体的pVT性质与气体的种类无关，因而一种理想气体的部分分子被另一种理想气体分子置换，形成的混合理想气体，其pVT性质并不改变，只是理想气体状态方程中的n此时为总的物质的量。15-03-1333pV=nRT=(nB)RT及pV=（m/Mmix)RT式中：m混合物的总质量Mmix混合物的摩尔质量又m=mB=nBMB=nyBMB=nMmixMmix=m/n=mB/nB即混合物的摩尔质量又等于混合物的总质量除以混合物的总的物质的量§1.2理想气体混合物的分压定律与分体积定律15-03-1334§1.2理想气体混合物的分压定律与分体积定律BBBmixMxM适用于气液固BBAABBAABBAMyMyMnnMnnnMnMnmAmixnM15-03-1335§1.2理想气体混合物的分压定律与分体积定律例某烟道气中各组分的体积分数792.0)(,077.0)(,131.0)(222NOCO求此烟道气在273.15K，101.325kPa下的体积质量。15-03-1336§1.3真实气体的状态方程（范德华方程）1.真实气体对理想气体的偏差压缩因子表示实际气体与理想气体之间偏差的物理量Z：nRTpVZRTpVZm或midmVVZ真实气体在某一确定状态下的摩尔体积与真实气体具有相同温度和相同压力的pg的摩尔体积15-03-1337§1.3真实气体的状态方程（范德华方程）Z＞1,则Vm＞Vmid，即同温同压下实际气体的摩尔体积大于理想气体的摩尔体积——真实气体比理想气体难于压缩Z＜1,则Vm＜Vmid，即同温同压下实际气体的摩尔体积大于理想气体的摩尔体积——真实气体比理想气体易于压缩对于理想气体：Z=100-7-28382.范德华方程nRTpVRTpVm分子间无相互作用力时气体的压力1mol气体分子的自由活动空间范德华考察了实际气体分子间有相互作用和分子本身有体积这两本质问题对PVT行为的影响，修正了理想气体方程，建立了范德华方程。§1.3真实气体的状态方程（范德华方程）邢台职业技术学院39Page2019年12月19日星期四WH实际气体：1)分子间有相互作用力内部分子器壁靠近器壁的分子分子间相互作用减弱了分子对器壁的碰撞，所以：p=p理-p内；p理=p+p内=p+a/Vm2压力修正项（内压力）p内=a/Vm2范氏常数§1.3真实气体的状态方程（范德华方程）邢台职业技术学院40Page2019年12月19日星期四WH2)分子本身占有体积1mol真实气体所能自由活动空间＝(Vm–b)§1.3真实气体的状态方程（范德华方程）(分子间无相互作用力时表现的压力)(1mol气体的可压缩空间)=RT3）范德华方程15-03-1341将修正后的压力和体积项引入理想气体状态方程：RTbVVapm2m范德华方程式中：a,b范德华常数，见附表1-1a为范氏常数，其值与各气体性质有关，均为正值。一般情况下，分子间作用力越大，a值越大。b：1mol分子由于自身所占体积,而使自由活动空间减小的值。a、b与气体温度无关。§1.3真实气体的状态方程（范德华方程）00-7-2842nRTnbVVanp22当p0,Vm,范德华方程理想气体状态方程若用nVVm代入以上方程，可得：§1.3真实气体的状态方程（范