必修4第三章三角恒等变形

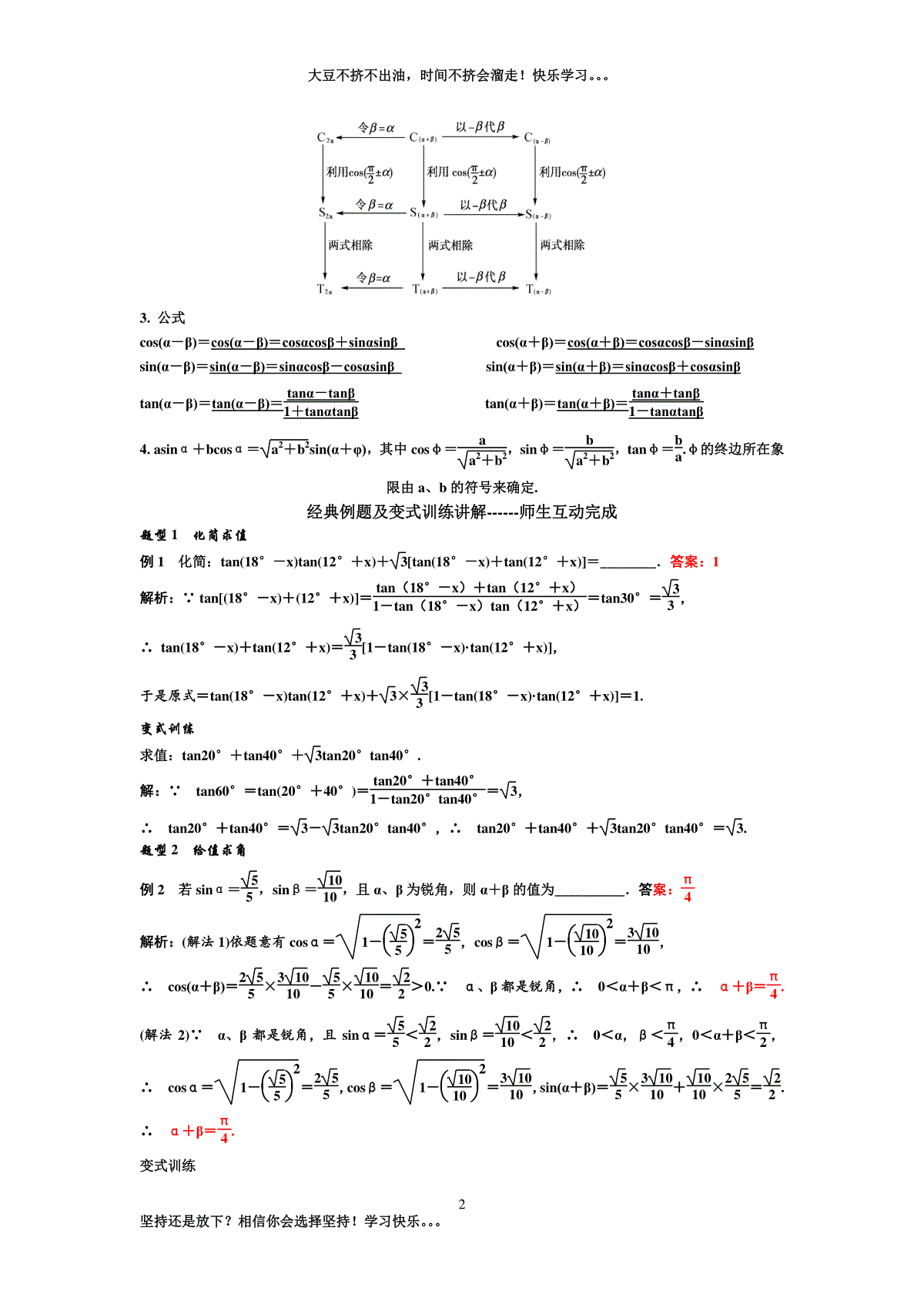
大豆不挤不出油，时间不挤会溜走！快乐学习。。。1坚持还是放下？相信你会选择坚持！学习快乐。。。必修（4）第三章三角恒等变换第1课时两角和与差的正弦、余弦和正切公式考情分析考点新知掌握两角和与差的三角函数公式，能运用两角和与差的正弦、余弦和正切公式进行简单的三角函数式的化简、求值及恒等式证明．①了解用向量的数量积推导出两角差的余弦公式的过程.②能从两角差的余弦公式推导出两角和的余弦、两角和与差的正弦、两角和与差的正切公式，体会化归思想的应用.1.sin75°cos30°－sin15°sin150°＝__________．答案：22解析：sin75°cos30°－sin15°sin150°＝sin75°cos30°－cos75°·sin30°＝sin(75°－30°)＝sin45°＝22.2.已知tanα－π6＝37，tanπ6＋β＝25，则tan(α＋β)＝________．答案：1解析：tan(α＋β)＝tan[(α－π6)＋(π6＋β)]＝tanα－π6＋tanπ6＋β1－tanα－π6·tanπ6＋β＝37＋251－37×25＝1.3.若sinα＝35，α∈－π2，π2，则cosα＋5π4＝__________．答案：－210解析：由α∈－π2，π2，sinα＝35，得cosα＝45，由两角和与差的余弦公式得cosα＋5π4＝cosαcos5π4－sinαsin5π4＝－22(cosα－sinα)＝－210.4.计算：2cos10°－sin20°cos20°＝________．答案：3解析：原式＝2cos（30°－20°）－sin20°cos20°＝2（cos30°cos20°＋sin30°sin20°）－sin20°cos20°＝232cos20°＋12sin20°－sin20°cos20°＝3.5.计算：sin7°＋cos15°·sin8°cos7°－sin15°·sin8°＝________．答案：2－3解析：sin7°＝sin(15°－8°)＝sin15°cos8°－cos15°sin8°，cos7°＝cos(15°－8°)＝cos15°cos8°＋sin15°sin8°，∴原式＝tan15°＝tan(45°－30°)＝1－tan30°1＋tan30°＝2－3.1.两角差的余弦公式推导过程2.公式之间的关系及导出过程大豆不挤不出油，时间不挤会溜走！快乐学习。。。2坚持还是放下？相信你会选择坚持！学习快乐。。。3.公式cos(α－β)＝cos(α－β)＝cosαcosβ＋sinαsinβcos(α＋β)＝cos(α＋β)＝cosαcosβ－sinαsinβsin(α－β)＝sin(α－β)＝sinαcosβ－cosαsinβsin(α＋β)＝sin(α＋β)＝sinαcosβ＋cosαsinβtan(α－β)＝tan(α－β)＝tanα－tanβ1＋tanαtanβtan(α＋β)＝tan(α＋β)＝tanα＋tanβ1－tanαtanβ4.asinα＋bcosα＝a2＋b2sin(α＋φ)，其中cosφ＝aa2＋b2，sinφ＝ba2＋b2，tanφ＝ba.φ的终边所在象限由a、b的符号来确定.经典例题及变式训练讲解------师生互动完成题型1化简求值例1化简：tan(18°－x)tan(12°＋x)＋3[tan(18°－x)＋tan(12°＋x)]＝________．答案：1解析：∵tan[(18°－x)＋(12°＋x)]＝tan（18°－x）＋tan（12°＋x）1－tan（18°－x）tan（12°＋x）＝tan30°＝33，∴tan(18°－x)＋tan(12°＋x)＝33[1－tan(18°－x)·tan(12°＋x)]，于是原式＝tan(18°－x)tan(12°＋x)＋3×33[1－tan(18°－x)·tan(12°＋x)]＝1.变式训练求值：tan20°＋tan40°＋3tan20°tan40°.解：∵tan60°＝tan(20°＋40°)＝tan20°＋tan40°1－tan20°tan40°＝3，∴tan20°＋tan40°＝3－3tan20°tan40°，∴tan20°＋tan40°＋3tan20°tan40°＝3.题型2给值求角例2若sinα＝55，sinβ＝1010，且α、β为锐角，则α＋β的值为__________．答案：π4解析：(解法1)依题意有cosα＝1－552＝255，cosβ＝1－10102＝31010，∴cos(α＋β)＝255×31010－55×1010＝22＞0.∵α、β都是锐角，∴0＜α＋β＜π，∴α＋β＝π4.(解法2)∵α、β都是锐角，且sinα＝55＜22，sinβ＝1010＜22，∴0＜α，β＜π4，0＜α＋β＜π2，∴cosα＝1－552＝255，cosβ＝1－10102＝31010，sin(α＋β)＝55×31010＋1010×255＝22.∴α＋β＝π4.变式训练大豆不挤不出油，时间不挤会溜走！快乐学习。。。3坚持还是放下？相信你会选择坚持！学习快乐。。。已知cosα＝17，cos(α－β)＝1314，且0＜β＜α＜π2，求β.解：∵0＜β＜α＜π2，∴0＜α－β＜π2.又cos(α－β)＝1314，∴sin(α－β)＝1－cos2（α－β）＝3314，∴cosβ＝cos[α－(α－β)]＝cosαcos(α－β)＋sinαsin(α－β)＝17×1314＋437×3314＝12.又0＜β＜π2，∴β＝π3.题型3给值求值例3已知0＜β＜π4＜α＜34π，cosπ4－α＝35，sin(3π4＋β)＝513，求sin(α＋β)的值．解：∵π4＜α＜3π4，∴－3π4＜－α＜－π4，∴－π2＜π4－α＜0.又cosπ4－α＝35，∴sinπ4－α＝－45.∵0＜β＜π4，∴3π4＜3π4＋β＜π.又sin3π4＋β＝513，∴cos3π4＋β＝－1213.∴sin(α＋β)＝－cosπ2＋（α＋β）＝－cos[(3π4＋β)－(π4－α)]＝－cos3π4＋βcosπ4－α－sin(3π4＋β)·sinπ4－α＝－()－1213×35－513×()－45＝3665＋2065＝5665.变式训练已知α、β∈0，π2，sinα＝45，tan(α－β)＝－13，求cosβ的值．解：∵α、β∈0，π2，∴－π2＜α－β＜π2.又tan(α－β)＝－13＜0，∴－π2＜α－β＜0.∴1cos2（α－β）＝1＋tan2(α－β)＝109.∴cos(α－β)＝31010，sin(α－β)＝－1010.又sinα＝45，∴cosα＝35.∴cosβ＝cos[α－(α－β)]＝cosαcos(α－β)＋sinαsin(α－β)＝35×31010＋45×－1010＝1010.例4已知α、β均为锐角，且sinα＝35，tan(α－β)＝－13.(1)求sin(α－β)的值；(2)求cosβ的值．解：(1)∵α、β∈0，π2，∴－π2＜α－β＜π2.又tan(α－β)＝－13＜0，∴－π2＜α－β＜0.∴sin(α－β)＝－1010.(2)由(1)可得，cos(α－β)＝31010.∵α为锐角，sinα＝35，∴cosα＝45.∴cosβ＝cos[α－(α－β)]＝cosαcos(α－β)＋sinαsin(α－β)＝45×31010＋35×－1010＝91050.变式训练大豆不挤不出油，时间不挤会溜走！快乐学习。。。4坚持还是放下？相信你会选择坚持！学习快乐。。。已知cosα＝13，cos(α＋β)＝－13，且α、β∈0，π2，求cos(α－β)的值．解：∵α∈0，π2，∴2α∈(0，π)．∵cosα＝13，∴cos2α＝2cos2α－1＝－79，∴sin2α＝1－cos22α＝429，而α、β∈0，π2，∴α＋β∈(0，π)，∴sin(α＋β)＝1－cos2（α＋β）＝223，∴cos(α－β)＝cos[2α－(α＋β)]＝cos2αcos(α＋β)＋sin2αsin(α＋β)＝()－79×()－13＋429×223＝2327.定时训练1.已知角φ的终边经过点P(1，－2)，函数f(x)＝sin(ωx＋φ)(ω＞0)图象的相邻两条对称轴之间的距离为π3，则fπ12＝__________．答案：－1010解析：由题意知cosφ＝55，sinφ＝－255.由相邻两条对称轴间距离为π3，得T2＝π3，即T＝2π3，∴2πω＝2π3，ω＝3.∴f(x)＝sin(3x＋φ)．fπ12＝sinπ4＋φ＝sinπ4cosφ＋cosπ4sinφ＝22×55＋22×－255＝－1010.2.函数f(x)＝sin2x·sinπ6－cos2x·cos5π6在－π2，π2上的单调递增区间为_________．答案：－5π12，π12解析：f(x)＝sin2xsinπ6－cos2x·cos5π6＝sin2xsinπ6＋cos2xcosπ6＝cos(2x－π6)．当2kπ－π≤2x－π6≤2kπ(k∈Z)，即kπ－5π12≤x≤kπ＋π12(k∈Z)时，函数f(x)单调递增．取k＝0得－5π12≤x≤π12，∴函数f(x)在－π2，π2上的单调增区间为－5π12，π12.3.已知sinα＋π3＋sinα＝－435，－π2＜α＜0，则cosα＝__________．答案：33－410解析：由sinα＋π3＋sinα＝－435，得sinα·cosπ3＋cosα·sinπ3＋sinα＝－435，∴32sinα＋12cosα＝－45，∴sinα＋π6＝－45.∵－π2＜α＜0，∴－π3＜α＋π6＜π6，∴cosα＋π6＝35.∴cosα＝cosα＋π6－π6＝cosα＋π6cosπ6＋sinα＋π6sinπ6＝35×32＋()－45×12＝33－410.4.设θ为第二象限角，若tanθ＋π4＝12，则sinθ＋cosθ＝________．答案：－105解析：由tanθ＋π4＝1＋tanθ1－tanθ＝12，得tanθ＝－13.因为θ为第二象限角，利用tanθ＝sinθcosθ，大豆不挤不出油，时间不挤会溜走！快乐学习。。。5坚持还是放下？相信你会选择坚持！学习快乐。。。sin2θ＋cos2θ＝1可求得sinθ＝1010，cosθ＝－31010，所以sinθ＋cosθ＝－105.5.已知α、β均为锐角，且tanβ＝cosα－sinαcosα＋sinα，则tan(α＋β)＝________．答案：1解析：∵tanβ＝cosα－sinαcosα＋sinα，∴tanβ＝1－tanα1＋tanα＝tan()π4－α.又∵α、β均为锐角，∴β＝π4－α，即α＋β＝π4，∴tan(α＋β)＝tanπ4＝1.6.已知cos()α－π6＋sinα＝453，则sin()α＋7π6的值为________．答案：－45解析：∵cos()α－π6＋sinα＝32cosα＋32sinα＝453，∴12cosα＋32sinα＝45，∴sin()α＋7π6＝－sin()α＋π6＝－32sinα＋12cosα＝－45.7如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别与单位圆相交于A、B两点．已知A、B的横坐标分别为210、255.求：(1)tan(α＋β)的值；(2)α＋2β的值．解：(1)由已知条件及三角函数的定义可知cosα＝210，cosβ＝255.因α为锐角，故sinα＞0，从而sinα＝1－cos2α＝7210，同理可得sinβ＝55.因此tanα＝7，tanβ＝12.所以tan(α＋