小初衔接暑假专题1-几何初步知识

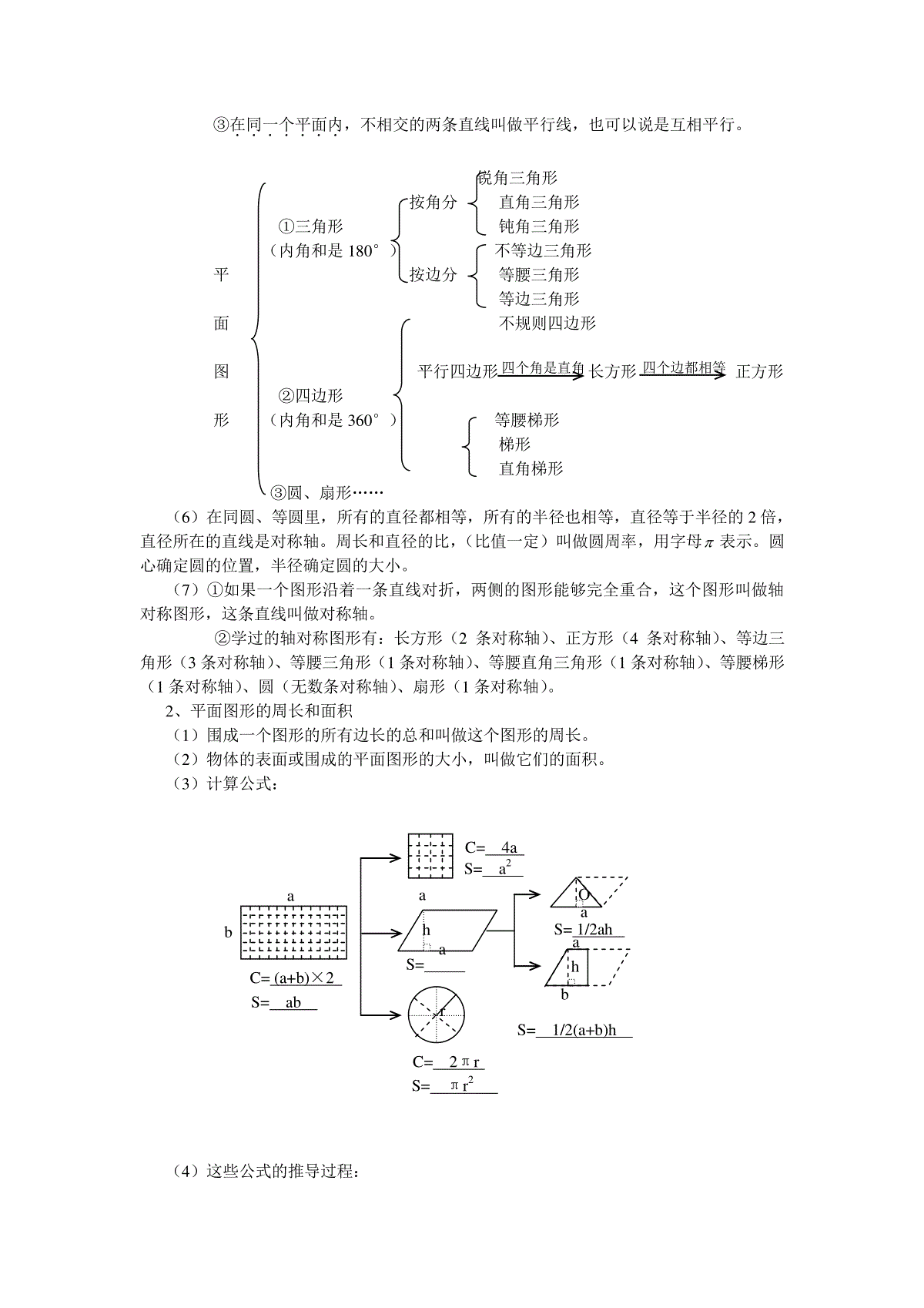
暑期专题辅导材料一【教学内容】小升初衔接课程——几何初步知识【教学目的】1、掌握直线、射线、线段三者之间的联系和区别；能熟练地辨别垂线与平行线以及常见的几种角；会画已知直线的平行线与垂线。2、掌握长方形、正方形、平行四边行、三角形、梯形、圆、长方体、正方体、圆柱、圆锥的主要特征；会画长方形、正方形、圆；进一步认识轴对称图形与对称轴。3、加深对平面图形的周长、面积、体积意义的理解；通过公式的推导，加深对辩证唯物主义事物都是联系的观点，使学生能熟练掌握已学过平面图形的周长、面积、立体图形的表面积体积公式计算，并能应用公式来解答一些实际问题。【知识讲解】1、平面图形的认识（1）点——直线——线段——射线用直尺把两点连接起来，就得到一条线段，把线段的一端无限延长，可以得到一条射线；把线段的两端无限延长，可以得到一条直线。（2）直线、射线和线段有什么联系和区别？名称图形特征备注直线没有端点，可以无限延长不可以度量射线有一个端点，可以向一端无限延长不可以度量线段有两个端点，长度是有限的可以度量（3）同一平面里两条直线的位置关系。平行——平行线锐角（小于90°）两直角——互相垂直——垂线条（等于90°）直相交——角钝角（大于90°小于180°）线平角（等于180°）周角（等于360°）重合（4）①角的大小要看两条边叉开的大小，叉开得越大，角越大。角的大小与角的两边画的长短没有关系。②两条直线相交成直角时，这两条直线互相垂直。③在同一个平面内．．．．．．．，不相交的两条直线叫做平行线，也可以说是互相平行。锐角三角形按角分直角三角形①三角形钝角三角形（内角和是180°）不等边三角形平按边分等腰三角形等边三角形面不规则四边形图平行四边形长方形正方形②四边形形（内角和是360°）等腰梯形梯形直角梯形③圆、扇形……（6）在同圆、等圆里，所有的直径都相等，所有的半径也相等，直径等于半径的2倍，直径所在的直线是对称轴。周长和直径的比，（比值一定）叫做圆周率，用字母表示。圆心确定圆的位置，半径确定圆的大小。（7）①如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形叫做轴对称图形，这条直线叫做对称轴。②学过的轴对称图形有：长方形（2条对称轴）、正方形（4条对称轴）、等边三角形（3条对称轴）、等腰三角形（1条对称轴）、等腰直角三角形（1条对称轴）、等腰梯形（1条对称轴）、圆（无数条对称轴）、扇形（1条对称轴）。2、平面图形的周长和面积（1）围成一个图形的所有边长的总和叫做这个图形的周长。（2）物体的表面或围成的平面图形的大小，叫做它们的面积。（3）计算公式：（4）这些公式的推导过程：四个角是直角四个边都相等C=4aS=a2C=(a+b)×2S=ababahaS=abhS=1/2(a+b)hS=1/2aharC=2πrS=πr2O1以梯形面积公式为例，把两个完全一样的梯形（如正面右下图所示）拼成一个平行四边形；可以看出这个平行四边形的底等于梯形上底加下底的和，高等于原来梯形的高；每个梯形的面积等于拼成的平行四边形面积的一半，所以梯形的面积=（上底+下底）×高÷2=hba)(21。3、立体图形的表面积和体积（1）一个立体图形所有的面的面积总和，叫做它的表面积。（2）一个立体图形所占空间的大小叫做它的体积。（3）长方体和正方体的特征：形体相同点不同点关系面棱点面的形状面积棱长长方体6个12条8个6个面都是长方形（也可能有两个相对的面的正方形）相对的面的面积相等每一组互相平行的四条棱的长度相等。正方体是特殊的长方体正方体6个12条8个6个面都是相等的正方形6个面的面积都相等12条棱的长度都相等。（4）圆柱和圆锥的特征：名称基本特征直圆柱1、上、下两个底面是面积相等的圆。2、两个底面之间的距离叫高，高垂直于上、下两个底面。3、圆柱的侧面展形是个长方形。（长=底面周长，宽=高）直圆锥1、底面是一个圆。2、从顶点到底面圆心的距离叫高，高垂直于底面圆。3、圆锥的体积等于和它等底、等高的圆柱体积的三分之一。（5）计算公式：262)(aSbhahabS正方体表长方体表2222rrhSchdhrhS圆柱表圆柱侧hSVaVabhV底圆柱正方体长方体3hSV底3312hrhSV底圆锥【典型例题】例1、下面几个图形中，哪些是直线？哪些是线段？哪些是射线？分析：直线、线段、射线首先必须是“直”的，不能有弯折。而判定一条“直”的线属于哪一种类型，依据就是端点的个数，如果没有端点，那么它就是直线；有一个端点，就是射线；有两个端点，它就是线段。答：（3）是直线，（2）是射线，（5）是线段。例2、求下图中角的度数。∠1=度∠2=度∠3=度解：先求出∠1的度数。（180°-150°=30°）再求出∠2的度数。（180°-30°-32°=118°）最后求出∠3的度数。（180°-118°=62°）例3、判断下列各题，正确的打“√”错的“×”。（1）直线AB长3厘米。………………………………………（）（2）角越大，角的边越大。……………………………………（）（3）不相交的两条直线叫平行线。……………………………（）（4）平行线间距离处处相等。…………………………………（）（5）黑板的边是垂线。…………………………………………（）分析与解：（1）因为直线是向两端无限延伸着的，它没有端点，所以无法度量。所以，原题是错的。（2）因为角的大小与边的长短无关，与角两边叉开大小有关。所以原题是错的。（3）因为原题没有强调“在同一平面内”这个前提，所以原题是错的。（4）此题是正确的。(1)(2)(3)(4)(5)12332°150°（5）因为垂直是指两条直线的相互位置关系，不能孤立地说某一条线是垂线。应该说“黑板的长边是短边的垂线”。所以原题是错的。例4、求右图的周长。（单位：分米）解：下图的周长包括长方形的两条长，一条宽与半圆弧长的总和。212014.320240)(4.13114.32080分米例5、已知梯形面积是12平方厘米，求阴影部分的面积。解法一：阴影部分是一个三角形，它的底是3厘米，要求它的面积，还需知道高，根据梯形面积的计算公式不难求出高。23)53(212)(5.4233平方厘米解法二：因为阴影部分与空白部分是两个等高的三角形，所以它们面积的比就是它们底边长的比，即3：5。由此可知，阴影部分的面积相当于梯形面积的533，阴影部分的面积可以直接求出。5.453312（平方厘米）例6、有一块长方形土地，长100米，宽是长的53，把这块地划出一个最大的正方形地种小麦，每公顷平均产小麦6吨。把全部小麦的51磨成面粉，小麦的出粉率是81%，可磨出面粉多少千克？（得数保留整千克。）分析：先求出长方形地的宽，即正方形小麦地的边长；进而求出正方形小麦地的面积，然后可以求出全部小麦的重量；再求出全部小麦的51是多少千克，最后求出这些小麦可以磨出面粉多少千克。解：（1）正方形小麦地的边长：6053100（米）（2）正方形小麦地的面积：36006060（平方米）3600平方米=0.36公顷（3）全部小麦的重量：402035千克吨2160)(16.236.06（4）磨面粉的小麦重是：432512160（千克）（5）磨出面粉的重量：35092.349%81432（千克）答：约可磨出面粉350千克。例7、有一个近似于圆锥的稻谷堆，底面周长是18.84米，高1.5米，把它装入一个底面积是7.8平方米的圆柱形粮囤正好装满，这个粮囤的高多少米？（保留一位小数）分析：把一个圆锥形的稻谷堆装入一个圆柱形的粮囤里正好装满，说明圆锥的体积正好等于圆柱的容积。解：8.75.1)14.3284.18(14.3312)(8.18.713.14米答：这个粮囤高约．1.8米。【跟踪练习】一、判断题：（正确的打“√”，错的打“×”）1、不相交的两条直线叫平行线。（）2、两个长方形周长相等，它们的面积必定相等。（）3、有一个角是锐角的三角形叫做锐角三角形。（）4、正方形的边长扩大3倍，它的面积就扩大6倍。（）5、半径是直径的一半，直径是半径的2倍。（）6、一个圆的周长与半径成正比例关系。（）7、扇形是轴对称图形，有无数条对称轴。（）8、决定圆锥体积大小的条件是底面半径和圆锥的高。（）9、一个棱长6分米的正方体，它的表面积与体积相等。（）10、等底等高的圆柱和圆锥，圆柱的体积比圆锥大2倍。（）二、填空题11、等腰三角形的顶角与一个底角的和是135°，它的顶角是（）度。12、一个正方形周长是0.4米，面积是（）平方米。13、一块平行四边形的面积是264平方米，它的高是12米，底是（）。14、一个圆的周长是6.28厘米，它的面积是（）。15、一个正方体的棱长是2厘米，它的表面积是（），体积是（）。16、两个棱长1分米的正方体木块，拼成一个长方体，这个长方体的表面积是（）。17、一个圆柱的底面直径和高都是10厘米，它的侧面积是（），表面积是（），体积是（）。18、一个圆锥和一个圆柱的底面积、体积都相等，如果圆锥的高是54厘米，圆柱的高是（）。19、如右图，∠1=（）°∠2=（）°∠3=（）°20、一个正方形，一边截去6厘米，另一边截去2厘米，剩下的长方形面积比原正方形面积少68平方厘米。原正方形的边长是（）。三、求下面各图形的阴影部分的周长和面积。（单位：厘米）21、22、23、四、求下面几何图形的体积。（单位：厘米）24、25、40°213O1OO22448OO1O2O321.50.86631五、应用题：26、一个长方形地，周长是50米，长是宽的1.5倍，这块地的面积是多少平方米？27、要制作一对．．圆柱形无盖铁皮水桶，底面周长是12.56分米，高是6分米，至少要用铁皮多少平方分米？（得数保留整数）28、有一个圆形鱼池，直径13米，紧沿着池边修一条宽2米的小道，小道面积是多少？29、一个圆锥形的碎石堆，底面半径1.8米，高1.5米。如果每立方米碎石重2.2吨，这堆碎石大约重多少吨？（得数保留整吨数）30、一个圆柱和一个圆锥等底等高，体积相差3.6立方分米，这个圆柱的体积是多少立方分米？31、用3个相同的正方体，粘接成一个长方体，长方体的棱长总和是40分米，这个长方体的表面积与体积各是多少？32、水结成冰时，冰的体积比水增加111。把一块长8分米，宽5分米，厚1.2分米的冰溶化在一只底面为8平方分米的圆柱形储水桶里，桶里水高与桶高的比为4：5，求圆柱形储水桶的高。参考答案与提示一、判断题：1、×2、×3、×4、×5、×6、√7、×8、√9、×10、√二、填空题：11、4512、0.0113、22米14、3.14平方厘米15、24平方厘米、8立方厘米16、10平方分米17、314平方厘米、471平方厘米、785立方厘米18、18厘米19、90°、50°、180°20、10厘米三、21、C=6.28厘米，S=0.86平方厘米22、C=18.84厘米，S=6.28平方厘米23、C=28.56厘米，S=19.44平方厘米四、24、94.2立方厘米25、3.6立方厘米五、应用题：26、10)5.11(250（米）……宽155.110（米）………………长1501510（平方米）…………面积27、2214.356.12（分米）……底面半径平方分米平方分米17684.1752)656.12214.3(228、5.6213（米）………………………内圆半径6.5+2=8.5（米）……………………外圆半径2.94)5.65.8(14.322（平方米）…………环形面积29、2368.55.18.114.3312（立方米）………圆锥形石堆的体积52096.112368.52.2吨12（吨）30、4.5)311(6.3（立方分米）31、2)2443(40（分米）……………………正方体的棱长24622（平方分米）…………………………表面积8222