当前位置:首页 > 电子/通信 > 综合/其它 > 041110211天线阵简单分析
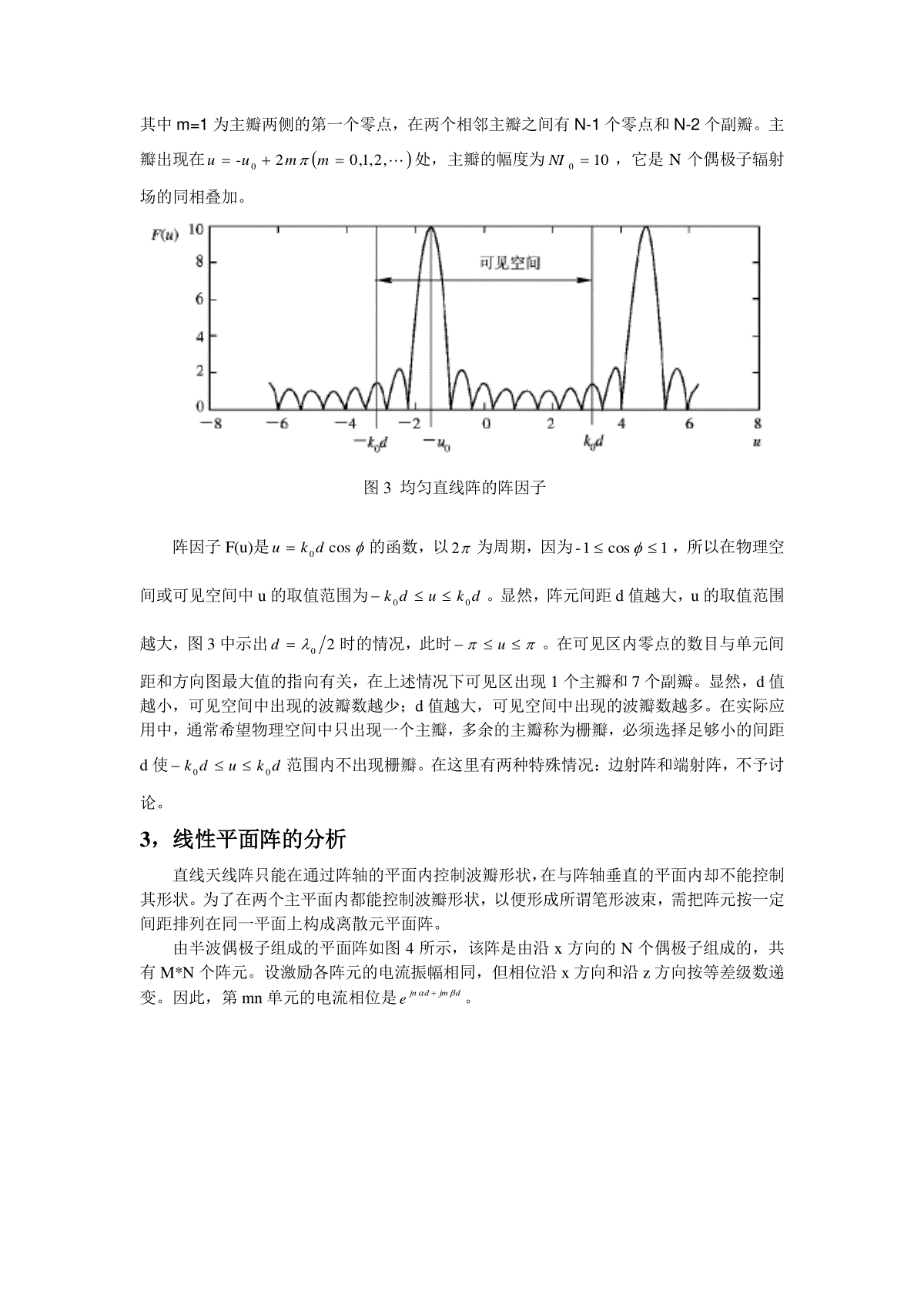
天线阵列简单分析041110211王之光摘要:本文先阐述了天线阵列的必要性,接着介绍了方向图相乘原理,然后对均匀直线阵和线性平面阵进行了着重分析,最后对立体阵进行了简单介绍。关键词:方向图相乘原理天线阵阵因子直线阵线性平面阵一,前言一般情况下,单个天线的增益不高,方向性不易控制。为了增强天线的方向性,提高天线的增益系数,或者为了得到所需的辐射特性,可以把若干个相同的辐射器按一定的规律排列起来,并给予适当激励,从而构成较为复杂的辐射系统,这样组成的辐射系统称为天线阵或阵列天线。组成天线阵的独立单元称为天线单元或阵元。阵元可以是任何类型的辐射器,如对称振子、缝隙天线、喇叭天线等,原则上阵元本身也可以是一个阵列。按阵元在空间的排列方式,天线阵可以分为线阵、平面阵和立体阵。按阵列的阵元分布方式,可分为离散阵列和连续阵列两类,前者可视为后者的采样近似。按阵元的间距,天线阵可分为均匀间距阵和非均匀间距阵。天线阵的辐射是干涉现象的特例,辐射特性取决于阵元的类型、数目、排列方式、阵元间距以及阵元上的电流的振幅和相位分布等。根据叠加原理,当存在多个频率相同、相位差恒定的波源时,空间任意一点的场是这些波源在该点产生的场的矢量叠加,结果空间某些方向上的场始终加强,另一些方向上的场则始终减弱,甚至完全消失。二,天线阵分析1,方向图相乘原理考虑图1所示的一般形式的天线阵,该天线阵是由N个天线组成的,一般来说,天线元的形式可以是各不相同的,但就常用的天线阵而言,天线元的形式和取向都是相同的。设第n个天线元位置矢量为nr,由相对振幅为nC、相对相位为n的电流激励,参考天线是位于坐标原点的01Cnn,的相同形式和取向的天线。设参考天线的辐射电场为refrrjk4,E0(1.1)式中,f为阵中单元天线的方向函数。在远区nrr,因此来自阵中所有天线的射线基本上是平行的,从第n个天线元到远区场点的距离可作如下近似:振幅因子中rRn。相位因子中必须考虑更高阶的近似:nrrrˆRn。因为当阵元间距足够大时,即使nR和r的差十分小,该差任然可能包含若干个波长,所以由这些相位差所产生的阵中各天线元在场点辐射场的相互干涉在控制天线阵的方向图中起着十分重要的作用。当考虑到阵中各天线元的不同传播相位滞后nrrjkeˆ0、不同激励振幅nC和激励相位nje时,阵中所有天线产生的总场可表示为N1ˆˆN100004,4,EnrrjkjnrjkrrjkrjknjnnnnneCrefrefeCr(1.2)比较式(1.1)和(1.2)可以看出,天线阵的方向函数,D可以表示成单元天线的方向函数,f和阵因子,F的乘积:,F,Df,(1.3)式中天线阵的方向性函数为N1ˆ0FnrrjkjnnneC,(1.4)上式即为天线阵的方向图相乘原理:一个天线阵的方向函数等于单个天线元的方向函数和阵方向函数的乘积。阵方向函数是阵中各天线元的位置、激励电流幅度和相位的函数。由于构成天线阵的阵元一般都具有很宽的方向图,阵的方向性主要由阵因子控制,因此在研究天线阵时通常只研究阵因子的作用。2,均匀直线阵分析各阵元排列在一条直线上就构成直线天线阵。各阵元取向一致,可沿任意方向。当各阵元激励电流幅度相等,相邻元相位差与间距均相等的相同元组成的直线阵称为均匀直线阵。图2为一个N元直线阵。假设该阵由间距为d的半波偶极子组成,各天线元的激励电图1任意N元阵流具有相同的的幅度0I及线性变化(按等差级数递变)的相位,各天线元间的相位差是ad,即dnn,这种天线阵称为均匀直线阵。设为rˆ与阵轴(x轴)的夹角,则cossincosrrˆnndnd,因此cos1-N000FndjkdjnneI,(2.1)使用几何级数的求和公式1-N0n11nn得dkdkNeIeeIdkNjdkjdkjNcos21sincos2sin11F00cos210coscos0000(2.2)令dudku00,cos,则阵因子的幅度可以写成00021sin2sinuuuuNIuF(2.3)这个函数除了具有周期性外,非常类似于非周期函数sinx/x。图3所示为N=10元阵阵因子的幅度随u的变化曲线,阵元电流幅度2,100uI。从曲线可见,方向图的零点位置为Nmudku2-cos00m=1,2,…,N-1(2.4)图2一维均匀直线阵其中m=1为主瓣两侧的第一个零点,在两个相邻主瓣之间有N-1个零点和N-2个副瓣。主瓣出现在,2,1,02-0mmuu处,主瓣的幅度为100NI,它是N个偶极子辐射场的同相叠加。阵因子F(u)是cos0dku的函数,以2为周期,因为1cos1-,所以在物理空间或可见空间中u的取值范围为dkudk00。显然,阵元间距d值越大,u的取值范围越大,图3中示出20d时的情况,此时u。在可见区内零点的数目与单元间距和方向图最大值的指向有关,在上述情况下可见区出现1个主瓣和7个副瓣。显然,d值越小,可见空间中出现的波瓣数越少;d值越大,可见空间中出现的波瓣数越多。在实际应用中,通常希望物理空间中只出现一个主瓣,多余的主瓣称为栅瓣,必须选择足够小的间距d使dkudk00范围内不出现栅瓣。在这里有两种特殊情况:边射阵和端射阵,不予讨论。3,线性平面阵的分析直线天线阵只能在通过阵轴的平面内控制波瓣形状,在与阵轴垂直的平面内却不能控制其形状。为了在两个主平面内都能控制波瓣形状,以便形成所谓笔形波束,需把阵元按一定间距排列在同一平面上构成离散元平面阵。由半波偶极子组成的平面阵如图4所示,该阵是由沿x方向的N个偶极子组成的,共有M*N个阵元。设激励各阵元的电流振幅相同,但相位沿x方向和沿z方向按等差级数递变。因此,第mn单元的电流相位是djmdjne。图3均匀直线阵的阵因子这种阵可以看成是M个N元直线阵组成的阵,按方向图相乘原理,平面阵阵因子等于x方向的N元直线阵的阵因子乘以z方向的M元直线阵的阵因子,即2sin2sin2sin2sin00000vvuuvvMuuNIvuF,(3.1)式中,dvdkvdudku0000,cos,,cossin。该阵因子的第一个最大值出现在00,vvuu处,这两个值确定了方向图主瓣在空间的方向。当0即各阵元同相馈电时,主瓣方向垂直于阵平面,即沿y方向,这种阵称为边射阵。当α和β取适当值时,主瓣可以指向任意的方向。对于边射阵,主瓣在xy平面和yz平面的零功率波瓣宽度可以通过令Nu21和uM21求得,其结果和均匀直线阵相同,MdBWNdBWyzxy00002,2(3.2)采用与直线阵相同的方法可求得半功率波瓣宽度dMBWdNBWyzxy05.005.065.2,65.2(3.3)方向性系数近似为202025.05.083.883.824AMNdBWBWDyzxy(3.4)图4线性平面阵式中A是平面阵面积。若不考虑天线的损耗,式(3.4)即为平面阵的增益公式。通常利用口径天线的增益公式估计平面阵天线的增益204AG(3.5)一个值得注意的问题是,当主瓣波束偏离阵面法向扫描时波束的宽度如何变化。设00cos0dkd,,即主瓣在xy平面内,其方向与x轴的夹角为0。在0附近将相位因子00coscosdk展开成泰勒级数,取其第一项,00000sincoscosdkdk(3.6)主瓣宽度由式(3.7)确定:0000sin212zzdkNuuN(3.7)下标z表示主瓣零点。因此主瓣宽度为dNNddNkBWzxy0000002sin2sin42(3.8)与式(3.2)相比较可以看出主瓣宽度增加了一个因子0sin1,即主瓣宽度变宽。注意0sindd为阵在垂直于波束方向上的投影长度,因此当主瓣波束方向偏离法向时,其方向图近似相当于原阵在垂直于波束方向上投影的阵的方向图。和直线均匀阵一样,要使线性平面阵在阵平面的每一边只产生单一主瓣,单元间距应小于0,否则会出现栅瓣。4,立体阵的简单介绍在与平面阵列平行的面上,设置一结构完全相同的M行*N列平面阵列(对应阵元位置有相同的x,y位置坐标),那么这两个平面阵列就将构成一新的阵列,它们的阵轴方向与z轴平行,这就构成了三维空间中的体阵。图5平面阵列图6所示为置于图5xy平面上的阵元纵横间距2yxdd,同相馈电的5行*5列,阵元及其空间取向均一的平面阵列三维标高阵函数图。图7则是以极坐标画出的该平面阵列在xz面(0)和yz面(90)的阵函数图,阵函数在这两个子午面上的方向图相同,在图中以实线表示,图中用虚线画出了45的子午面的阵函数图。该图中极坐标标度是以阵函数的最大值作为0dB。参考文献:【1】ConstantineA.Balanis,“AntennaTheory”JoinWiley&Sons,Inc.2005【2】卢万铮,“天线理论与技术”西安电子科技大学出版社2004.5【3】殷际杰,“微波技术与天线”电子工业出版社2004.6【4】马汗炎,“天线技术”哈尔滨工业大学出版社2000.6【5】闫映红,“天线与电波传播理论”清华大学出版社;北京交通大学出版社2005.11图6立体阵图7极坐标下的阵函数图


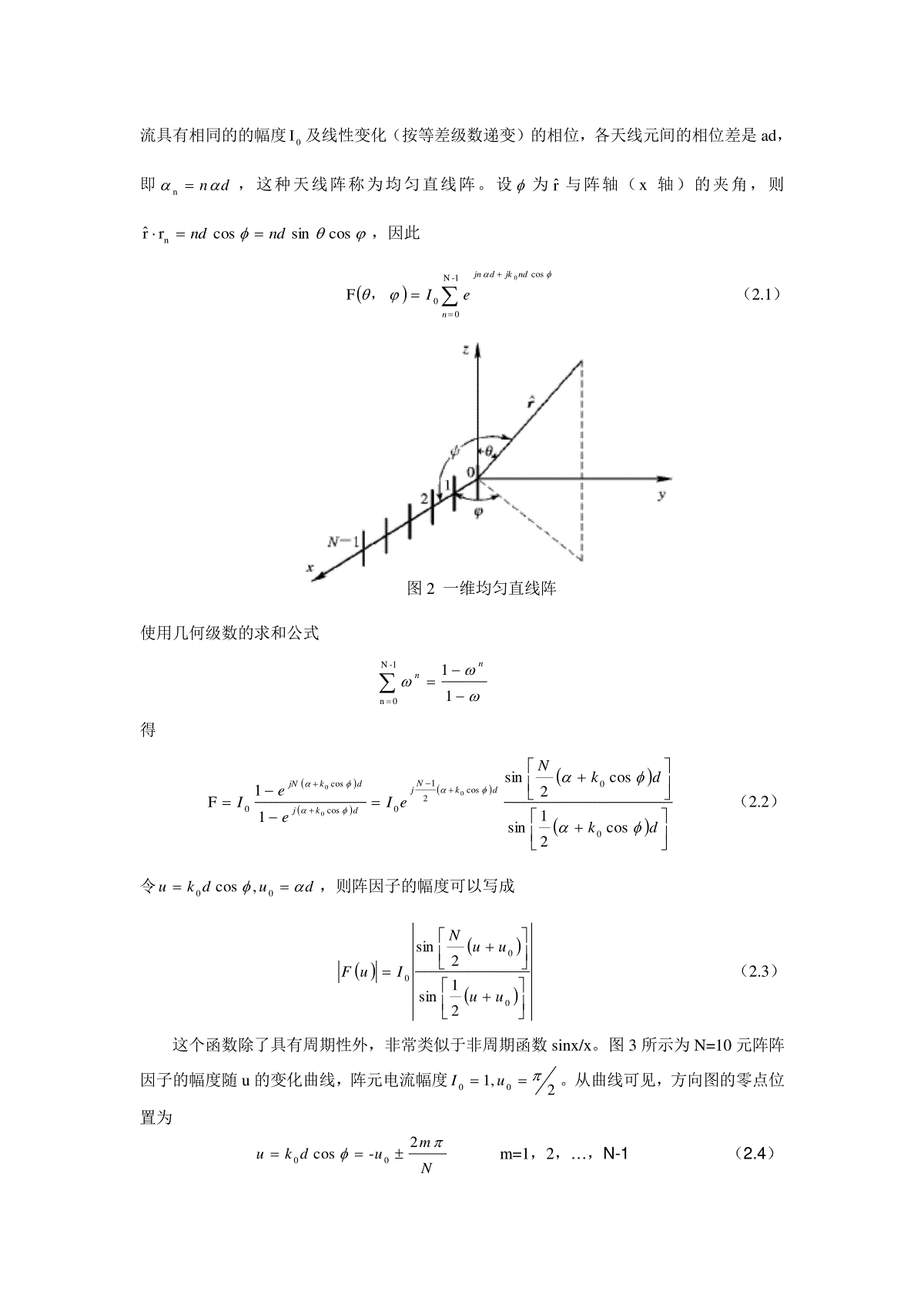

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:041110211天线阵简单分析
链接地址:https://www.777doc.com/doc-3050746 .html