搜索
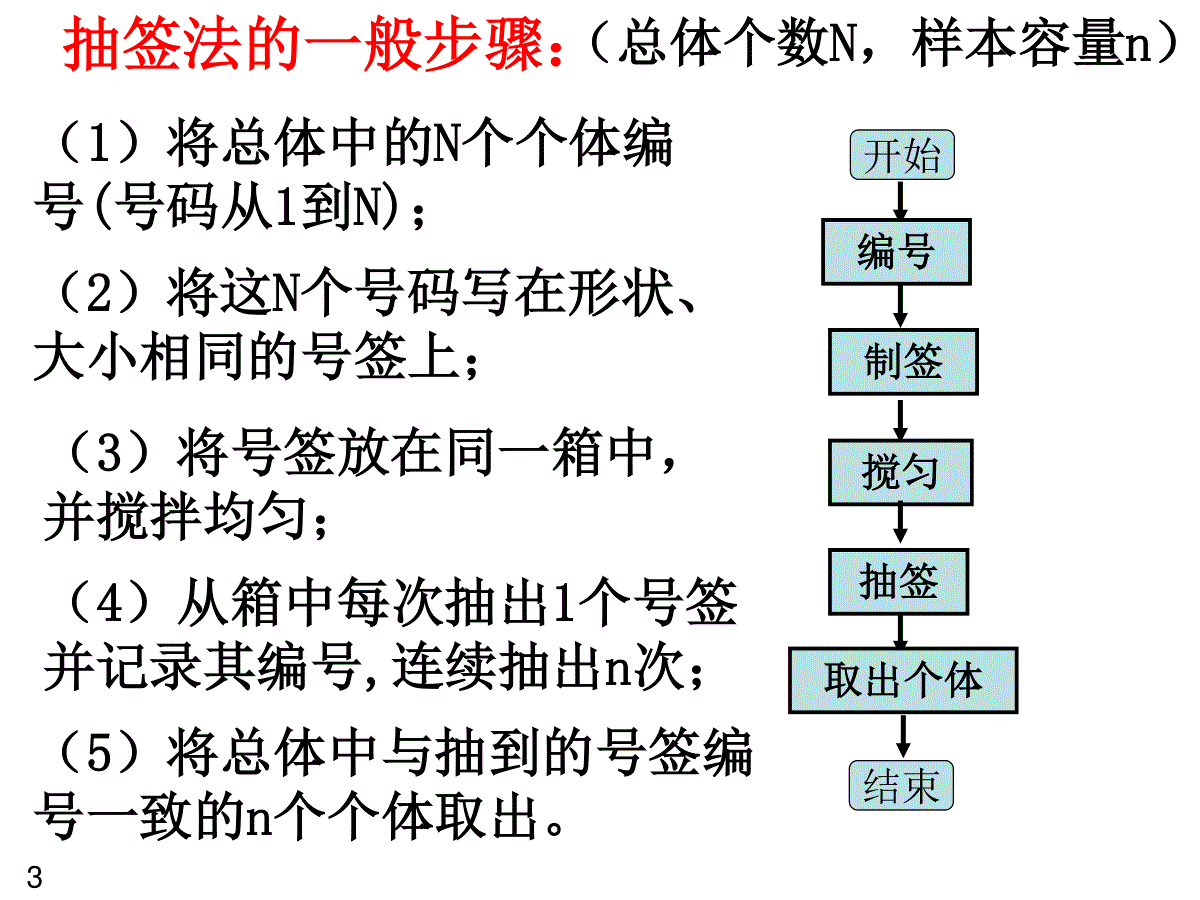
（1）它要求被抽取样本的总体的个体数有限；（2）它是从总体中逐个进行抽取；（3）它是一种不放回抽样；（4）它是一种等概率抽样.一般地，设一个总体的个体数为N，如果通过逐个不放回地抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样.1、简单随机抽样1一、复习回顾（5）如果用从个体数为N的总体中抽取一个容量为n的样本，那么每个个体被抽取的概率等于Nn2抽签法随机数表法简单随机抽样2.抽签法(抓阄法)把总体中的N个个体编号，并把号码写在形状、大小相同的号签上，将号签放在同一个容器里，搅拌均匀后，每次从中抽出1个号签，连续抽取n次，得到一个容量为n的样本。抽签法的一般步骤：（1）将总体中的N个个体编号(号码从1到N)；（2）将这N个号码写在形状、大小相同的号签上；（3）将号签放在同一箱中，并搅拌均匀；（4）从箱中每次抽出1个号签并记录其编号,连续抽出n次；（5）将总体中与抽到的号签编号一致的n个个体取出。（总体个数N，样本容量n）开始编号制签搅匀抽签取出个体结束3步骤①将总体中的所有个体编号(每个号码位数一致);②在随机数表中选定开始的数字(确定行数列数);③从选定的数开始按一定方向读数，若得到的号码大于总体编号或与前面所取出的号码重复的去掉，如此进行下去，直到取满为止;④根据选定的号码抽取样本。3.随机数法4问题1：某校为了了解高二年级学生对教师教学的意见，打算从高二年级500名学生中抽取50名进行调查。请你设计出抽取样本的方法？简单随机抽样适用于个体数不太多的总体。那么当总体个体数较多时，这种方法的实施起来就比较困难问：采用什么抽样方法比较好？问题提出5分析：我们按这样的方法来抽样：首先将这５００名学生从１开始进行编号，然后按号码顺序以一定的间隔进行抽取。由于＝１０，这个间隔可以定为１０，即从号码为１－１０的第一个间隔中随机地抽取一个号码，假如抽到的是６号，然后从第６号开始，每隔１０个号码抽取一个，得到６，１６，２６，３６，…，４９６。这样就得到一个容量为５０的样本50050这种抽取方法是系统抽样。62.1.2~2.1.3系统抽样、分层抽样1、系统抽样1）定义：现将总体中的个体逐一编号，然后按号码顺序以一定的间隔k进行抽取，先从第一个间隔中随机地抽取一个号码，然后逐个抽取的号码依次增加间隔数即得到所求样本。二、新课教学2）系统抽样的步骤：①、采用随机的方式将总体中的个体编号为简便起见，有时可直接采用个体所带有的号码，如考生的准考证号、街道上各户的门牌号，等等8问题：当总体不能被样本容量整除时怎么办？②、为将整个的编号分段（即分成几个部分），要确定分段的间隔k,当N/n（N为总体中的个体的个数，n为样本容量）是整数时，k=N/n;当N/n不是整数时，通过从总体中剔除一些个体使剩下的总体中个体的个数N'被n整除，这时k=N'/n.③、在第一段用简单随机抽样确定起始的个体④、按照事先确定的规则抽取样本（通常是将加上间隔k，得到第2个编号+k,第3个编号+2k，这样继续下去，直到获取整个样本）9（4）系统抽样所得样本的代表性和具体的编号有关；而简单随机抽样所得样本的代表性与个体的编号无关，如果编号的个体特征随编号的变化呈现一定的周期性，可能会使系统抽样的代表性很差；系统抽样说明(1)、适用于总体中个体数较大且个体差异不明显的情况（2）、剔除多余个体及第一段抽样都用简单随机抽样，因而与简单随机抽样有密切联系（3）、是等可能抽样，每个个体被抽到的可能性相等10学案51页例题1例1．（1）先用简单随机抽样剔除3人；（2）把余下的人编号：000-999，并分成20组，每组50人；（3）在第一组用简单随机抽样抽取1人，设为k，以后各组依次取k+50，k+100，k+150，……，k+950．问题2：假设某地区有高中生2400人，初中生10900人，小学生11000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因，要从本地区的中小学生中抽取1%的学生进行调查.你认为应当怎样抽取样本？1）定义：总体由差异明显的几部分组成时，为了使样本更充分地反映总体的情况，常将总体分成几个部分，然后按照各部分所占的比例进行抽样，这种抽样叫做“分层抽样”，其中所分成的各部分叫做“层”.2、分层抽样112）分层抽样的步骤：(1)将总体按一定的标准分层；(2)计算各层的个体数与总体的个体数的抽样比k=n/N；(5)综合每层抽样，组成样本.(4)在每一层中按步骤3确定的数目进行抽样;（可用简单随机抽样或系统抽样)开始分层计算比定层抽取容量抽样组样结束(3)确定第i层应该抽取的个体数目使得各之和为NkNniiiN12三、巩固运用例1某中学有高一学生322名，为了了解学生的身体状况，要抽取一个容量为40的样本，应如何抽样？写出抽样过程第一步，随机剔除2名学生，把余下的320名学生编号为1，2，3，…320.第二步，把总体分成40个部分，每个部分有8个个体.解第三步，在第1部分用抽签法确定起始编号.第四步，从该号码起，每间隔8个号码抽取1个号码，就可得到一个容量为40的样本.13例2、一个地区共有5个乡镇，人口3万人，其中人口比例为3∶2∶5∶2∶3.从3万人中抽取一个300人的样本，分析某种疾病的发病率，已知这种疾病与不同的地理位置及水土有关，问应采取什么样的方法？并写出具体过程．解：因为疾病与地理位置和水土均有关，所以不同乡镇的发病情况差异明显，因而采用分层抽样的方法，具体过程如下：(1)将3万人分为5层，其中一个乡镇为一层．14(2)、按照样本容量的比例随机抽取各乡镇应抽取的样本．300×3/15＝60(人)，300×2/15＝40(人)，300×5/15＝100(人)，300×2/15＝40(人)，300×3/15＝60(人)，因此各乡镇抽取的人数分别为60人、40人、100人、40人、60人．(3)、将300人组到一起，即得到一个样本．注意：1、分层抽样适用于总体由差异明显的几部分组成的情况，每一部分称为层，在每一层中实行简单随机抽样。152、分层抽样中分多少层，要视具体情况而定。总的原则是：层内样本的差异要小，而层与层之间的差异尽可能地大，否则将失去分层的意义。练习：选择合适的抽样方法进行抽样(1)有30个篮球，其中甲厂生产的有21个，乙厂生产的有9个，从中抽取10个(2)有甲厂生产的300个篮球，抽取10个。(3)有甲厂生产的30000个篮球从中抽取10个。分层抽样简单随机抽样系统抽样16学案52页例2、例3简单随机抽样、系统抽样、分层抽样的比较类别共同点各自特点联系适用范围简单随机抽样（1）抽样过程中每个个体被抽到的可能性相等（2）每次抽出个体后不再将它放回，即不放回抽样从总体中逐个抽取总体中个体较少将总体平均分成几部分，按预先制定的规则在各部分抽取在起始部分时采用简单随机抽样总体中个体较多系统抽样将总体分成几层，分层进行抽取各层抽样时采用简单随机抽样或系统抽样总体由差异明显的几部分组成分层抽样17课堂练习3、从2005个编号中抽取20个号码入样，采用系统抽样的方法，则抽样的间隔为（）A、99B、99.5C、100D、100.5C181、系统抽样适合的总体应是（）A、容量较小的总体；B、容量较大的总体；C、个体数较多但均衡的总体；D、任何总体C2、要从已编号（1~50）的50件产品中随机抽取5件进行检查，用系统抽样可能的编号是（）A、5，10，15，20，25B、3，13，23，33，43C、1，2，3，4，5，D、2，4，8，16，32B194、某单位有职工160人，其中业务员有104人，管理人员32人，后期24人，现用分层抽样从中抽取一容量为20的样本，则抽取管理人员（）人A、3B、4C、7D、12B5、某校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本，已知女学生中抽取的人数为80，则N=1926、某大学数学系共有本科生5000人，其中一、二、三、四年级的学生比为4：3：2：1，用分层抽样的方法抽取一个容量为200人的样本，则应抽取三年级的学生为（）人。A、80B、40C、60D、20B达标练习：1、为了解1200名学生对学校某项教改试验的意见，打算从中抽取一个容量为30的样本，考虑采用系统抽样，则分段的间隔k为（）A、40B、30C、20D、122、为了了解参加一次知识竞赛的1252名学生的成绩，决定采用系统抽样的方法抽取一个容量为50的样本，那么总体中应随机剔除的个体数目（）A、2B、4C、5D、6AA3、用系统抽样的方法从个体数为1003的总体中抽取一个容量为50的样本，在整个抽样过程中每个个体被抽到的可能性为（）A、1/1000B、1/1003C、50/1003D、50/10004、从N个编号中抽取n个号码入样，用系统的方法抽样，则抽样的间隔为（）A、N/nB、nC、[N/n]D、[N/n]+1说明：[N/n]表示N/n的整数部分。5、从已编号为1－50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验，若采用每部分选取的号码间隔一样的系统抽样方法，则所选取5枚导弹的编号可能为（）A、5，10，15，20，25B、3，13，23，33，43C、1，2，3，4，5D、2，4，6，16，32CCB6、※(2004年福建省高考卷)一个总体中有100个个体，随机编号为0，1，2，…99，依编号顺序平分成10个小组，组号依次为1，2，3，…，10。现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m，那么在第k组中抽取的号码个位数字与m＋k的个位数字相同。若m＝6，则在第7组中抽取的号码为63解析:依编号顺序平均分成的10个小组分别为0~9,10~19,20~29,30~39,40~49,50~59,60~69,70~79,80~89,90~99.因第7组抽取的号码个位数字应是3,所以抽取的号码是63.这个样本的号码依次是6,18,29,30,41,52,63,74,85,96这10个号.2）.系统抽样适合于总体的个体数较多的情形，操作上分四个步骤进行，除了剔除余数个体和确定起始号需要随机抽样外，其余样本号码由事先定下的规则自动生成，从而使得系统抽样操作简单、方便.四、小结或作业1）.系统抽样也是等概率抽样，即每个个体被抽到的概率是相等的，从而保证了抽样的公平性.201、小结4）.分层抽样是按比例分别对各层进行抽样，再将各个子样本合并在一起构成所需样本.其中正确计算各层应抽取的个体数，是分层抽样过程中的重要环节.3）.分层抽样利用了调查者对调查对象事先掌握的各种信息，考虑了保持样本结构与总体结构的一致性，从而使样本更具有代表性，在实际调查中被广泛应用.5）.简单随机抽样是基础，系统抽样与分层抽样是补充和发展，三者相辅相成，对立统一.21