新人教版-七年级上册初一数学期末总复习课件

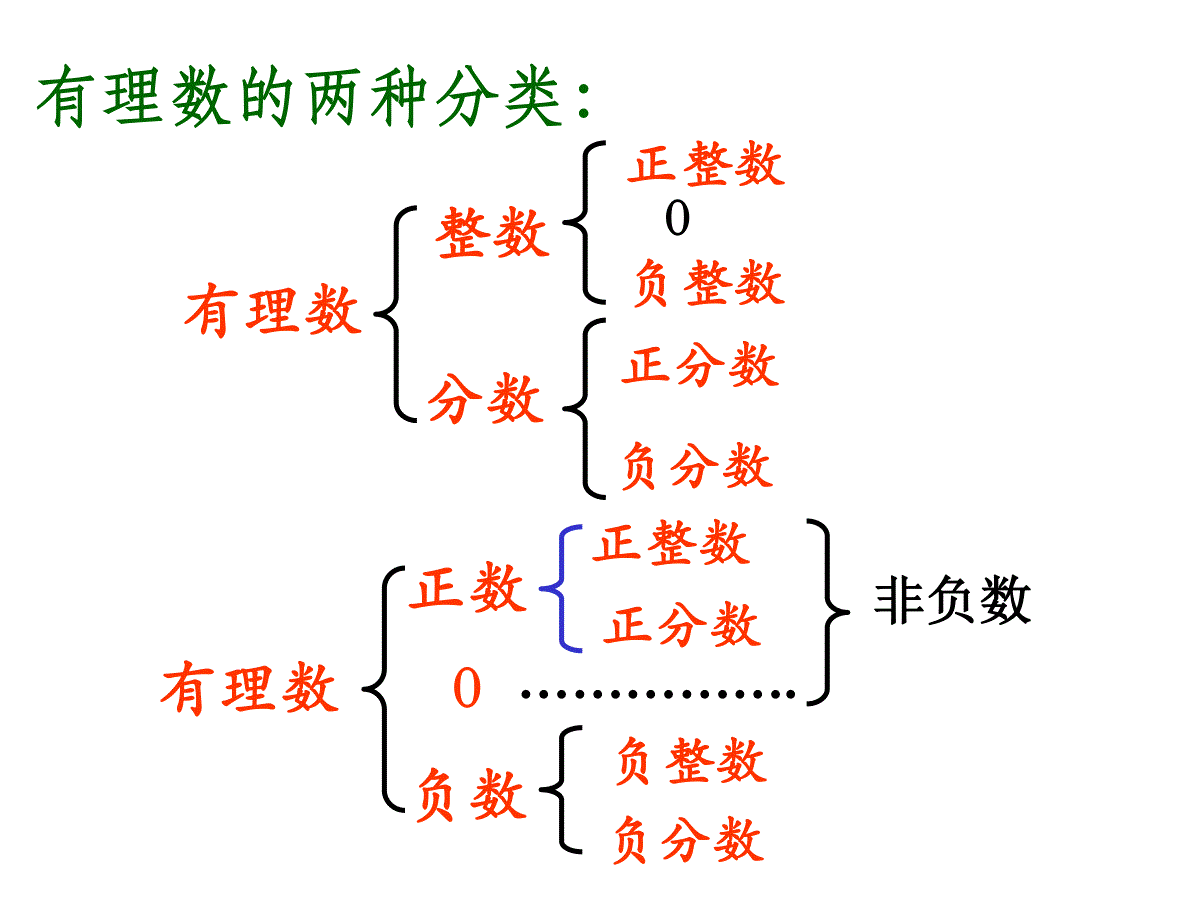
总复习进步仍然垂手可得，只要你努力！一切在你手中，你准备好了吗？子曰:学而时习之,不亦说乎!Yourself！Yourself！谁是你进步的最大障碍？谁是你进步的决策者？有理数的两种分类：正整数0有理数负整数正分数负分数分数整数正数负数正整数正分数有理数负整数负分数0…………….非负数8、把下列各数分别填在相应的集合里：-10，6，-5，40，-8，-(-3),0，-14，正数集合：,)31(-,26.0负数集合：｛-10，-8,-14,，···｝43整数集合：分数集合：,6.0,432)31(-｛，,···｝6.0,2)31(-43｛6,-5，40，-(-3),···｝｛-10，6,-5，40，-8，-(-3),0，-14,···｝非负数数集合：｛6,-5，40，-(-3),0,···｝,)31(-,26.0数轴:规定了原点、正方向、单位长度的直线如上图：A点表示＿＿；B点表示＿＿；C点表示＿＿；D点表示＿＿：E点表示＿＿。任何一个有理数都可以用数轴上的一个点来表示。相反数a-a1倒数1.只有符号不同的两个数。2.互为相反数的两个数相加得两个互为相反数的商是03.乘积是1的两个数。3的倒数是－4的倒数是-3.25的倒数是互为倒数的两个数相乘得1-1一个数a的相反数是3的相反数是()－4的相反数是()0的相反数是()0没有倒数.一个数a(a≠0)的倒数是一个数的绝对值就是表示这个数的点到原点的距离。数a的绝对值记为｜a｜1)正数的绝对值是它本身；2)0的绝对值是0；3)负数的绝对值是它的相反数。绝对值：｜a｜a-a0a＞0a=0a＜0｜-2.1｜=｜5｜=32关于化简绝对值如何化简绝对值符号例：a、b、c在数轴上的位置如图化简|c－b|＋|a－c|－|b＋c|c0ba∵c－b是负数，∴|c－b|＝－（c－b）∵a－c是正数，∴|a－c|＝a－c∵b＋c是负数，∴|b＋c|＝－（b＋c）原式=－（c－b）＋（a－c）－[－（b＋c）]＝a+b－c1、一个数的绝对值是6,这个数是＿＿＿。2、绝对值小于3的整数有＿＿＿个。3、的相反数的倒数是＿＿＿＿。4、计算：＿＿＿。5、如果,那么a=。6、如果规定上升8米记作8米，那么－7米表示_______________。7、最小的正整数是____,最大的负整数是_____,绝对值最小的有理数是_______911-=0×2×1-22002)()(-16=2a6±510904±下降7米1－10大显身手五个有理数的积为负数，则五个数中负数的个数是（）A.1B.3C.5D.1或3或5一个数的立方等于它本身，这个数是（）A.0B.1C.－1，1D.－1，1，0DD在数轴上,原点两旁与原点等距离的两点所表示的数的关系是().A、相等B、互为相反数C、互为倒数D、不能确定如果一个数的相反数比它本身大，那么这个数为().A、正数B、负数C、非负数D、不等于零的有理数BB在有理数中，倒数等于本身的数有（）.A、1个B、2个C、3个D、无数个B下列说法正确的是().A、正数与负数统称为有理数B、带负号的数是负数C、正数一定大于0D、最大的负数是－1C一.选择题:1.下列说法正确的是()A.一个数前面加上“－”号这个数就是负数;B.非负数就是正数;C.正数和负数统称为有理数;D.0既不是正数也不是负数；A.1个B.2个C.3个D.4个).(,511+(-,32-,1+-,7--,(-2)-2负数有中在).检测题DC3.一个数的倒数是它本身的数是().A.1B.-1C.±1D.04．下列计算正确的是().A.(-4)2=-16B.(-3)4=-3434-=)31D.(-1251=51-43-).(C5.(-0.2)2002×52002+(-1)2002+(-1)2001的值是().A.3B.-2C.-1D.1CCD6.如果两个数的绝对值相等,那么这两个数是().A.互为相反数;B.相等;C.积为0;D.互为相反数或相等.7.下列说法正确的是().A.若两个数互为相反数,则这两个数一定是一个正数,一个负数;B.一个数的绝对值一定不小于这个数;C.如果两个数互为相反数,则它们的商为-1;D.一个正数一定大于它的倒数.DB8.若a0,b0,则下列各式正确的是().A.a-b0;B.a-b0;C.a-b=0;D.(-a)+(-b)0.9.若0a1,则a,).(12从小到大排列正确的是a,aA.a2aa1B.aa1a2D.aa2a110.在数轴上距2.5有3.5个单位长度的点所表示的数是().A.6B.-6C.-1D.-1或6a1C.aa2DAD1１.当n为正整数时,(-1)-(-1)的值是().A.0B.2C.-2D.2或-22n+12nC12.已知，则：03)2(2yxx2yx-1提示：平方和绝对值的非负性．即：20,0aa∵(x+2)2≥0,︱x-y+3︱≥0∴(x+2)2＝003)2(2yxx且︱x-y+3︱＝0即：x+2＝0，x-y+3＝0解之得:x=-2,y=1二．填空题:13.对某种盒装牛奶进行质量检测,一盒装牛奶超出标准质量2克,记作+2克,那么-3克表示=_____________________________.14.有理数2，+7.5，-0.03，-0.4，0，31中,非负数是______________.15.如果-x=-(-12),那么x=_____.16.化简|3.14－π|=_________.17.计算:(－53+32+52-31)()()--=___.一盒装牛奶低于标准质量3克310572,,.,+-12π-3.14018.在－(-2),－|-2|,(-2)2,-22四个数中,负数有_____个.19.如果x0,且x2=25,那么x=____.32(-3))51(-32-041，，，,21.计算:－3×23-(-3×2)3=____.按从小到大排列的顺序是___________________.22.若|x|=3,则x=_____.20.把2-541,51-,0,32--323)(,)(192±323.水池中的水位在某天八个不同时间测得记录事下:(规定向上为正,向下为负,单位:厘米)+3,-6，-1，+5，-4，+2，-3，-2，那么这天中水池中水位的最终变化情况是__________.24.如果x2=4,那么x=______.三.计算题:25.①计算:(-3)×(-9)－8×(-5)②计算:－63÷7+45÷(-9)下降6厘米-2或2=67=-14③计算:(－3)x-(-3×2)223=204五袋白糖以每袋50千克为标准，超过的记为正,不足的记为负,称量记录如下：＋4.5，－4，＋2.3，－3.5，＋2.5（1）这五袋白糖共超过多少千克？（2）总重量是多少千克？解:(1)＋4.5－4＋2.3－3.5＋2.5=1.8(千克)(2)50×5＋1.8=251.8(千克)一杯饮料,第一次喝了一半,第二次喝了剩下的一半,…如此喝下去,第五次喝后剩下的饮料是原来的几分之几?321=521)(④计算:(-0.1)3－2)53(×41－⑤计算:433(-1)-(-2)×3-2-⑥计算:(－62)21(÷)250(+|-3|÷32×23.)⑦计算:［11×2－|3÷3|-(-3)2-33］÷43⑧计算:222340÷)21()21(-1×92..－－100089==15233==-20233-=（1）两个互为相反数的数的和是；（2）两个互为相反数的数的商是（0除外）的相反数是，倒数是，绝对值是．（3）平方等于本身的数是_______.绝对值等于本身的数是_______.立方等于本身的数是_______.（4）倒数等于它本身的数是_______.没有倒数的数是_______（5）____的平方是4，_____的绝对值是4；用心填一填213(6)有理数有两种不同的分类，它们是（）•A、正数,负数或整数,小数B、零,自然数或正数,负数•C、自然数，分数或正有理数，负有理数和零•D、整数，分数或正有理数，负有理数和零Ｄ耐心选一选1.关于“零”，下列说法错误的是……………………()（A）是整数也是有理数（B）不是正数，也不是负数（C）是整数也是自然数（D）不是自然数2.如果两个数的乘积是负数，和是正数。那么这两个数的关系是----------------------------（）（A）两个都正（B）两个都负（C）一正一负且负的绝对值较大（D）一正一负且正的绝对值较大ＢＤ３．互为相反数，下列各组数中不是互为相反数的是（）A.B.C.D.ba和ba,44ba和33ba和22ba和D(3)数字通常写在字母前面;代数式:是用基本运算符号把数字、表示数的字母连接起来的式子。注意：1、单独一个数或一个字母也是代数式。2、式子不含“=”、“”、“”、“≤”、“≥”(1)a×b通常写作a·b或ab；（运算符包括加、减、乘、除、乘方）a1(2)1÷a通常写作;如：a×3通常写作3a(4)带分数一般写成假分数.511如：×a通常写作a56代数式的规范写法像4+3(x-1),x+x+(x+1),a+b,ab,2(m+n),a3等式子都是代数式.*单项式的次数•一个单项式中，所有字母的指数的和叫做这个单项式的次数。说明：（1）是所有的字母，不是部分字母；（2）是指数的和，不是指数的乘积。例如：abc的所有字母是a,b,c，它们的指数都是1，指数和是1+1+1=3，所以abc的次数是3，它是三次单项式。4x²yz的所有字母是x,y,z，它们的指数和是2+1+1=4，所以4x²yz的次数是4，它是四次单项式。几个单项式的和叫做多项式。在多项式中，每个单项式叫做多项式的项。其中，不含字母的项,叫做常数项。例如，多项式3x²–2x+5有三项，它们是3x²，–2x，5。其中5是常数项。一个多项式含几项，就叫几项式。多项式里次数最高项的次数，就是这个多项式的次数。例如，多项式3x²–2x+5是一个二次三项式。*多项式及相关概念（1）几个单项式的和叫做_________.（2）在多项式中，每个单项式叫做___________.（3）在多项式中，不含字母的项叫做_______.（4）在多项式中，次数最高的项的次数，叫做这个______________.（5）多项式的每一项是否包括它前面的符号？（6）单项式的次数与多项式的次数有什么区别？多项式多项式的项常数项多项式的次数多项式的每一项都包括它前面的符号，有正号也有负号。单项式的次数是所有字母的指数的和；多项式的次数不是所有项的和。分清哪些是同类项是合并同类项的关键。合并同类项时注意：1、同类项合并过程中，把同类项的系数相加，字母和字母的指数不变。不是同类项不可以合并。2、在求代数式的值时，可先合并同类项将代数式化简，然后再代入数值计算，这样往往会简化运算过程。（1）所含字母相同，（2）相同字母的指数也相同。同类项合并同类项：89284252312abbabbaba在含较多项的代数式中合并同类项，为避免重复或遗漏，可先在同类项下面做上相同的记号再进行合并，合并的项在移动时，符号要一起移。判断和合并同类项的口诀：同类项，须判断，两相同，是条件；合并时，须计算，系数加，两不变。注意：1）合并同类项只是系数相加，字母与字母的指数不变；2）不是同类项的不能合并。括号前面是“+”号，去掉括号和它前面的“+”号，括号里面各项不变号；括号前面是“—”号，去掉括号和它前面的“—”号，括号里面各项要变号。6m2+(m2–2m)–(2m2—5m)=6m2+m2–2m–(2m2–5m)+=6m2+m2–2m–2m2+5m+=（6m2+m2–2m2）+(–2m＋5m)=（6+1–2）m2+(–2＋5)m=5m2+3m+第二章|复习考点攻略数学·人教版（RJ）►考点一整式的有关概念例1在式子3m＋n,－2mn,p,x－b2，0中，单项式的个数是()A．3B．4C．5D．6A错误警示：单项式的次数和系数、多项式