当前位置:首页 > 中学教育 > 高中教育 > 上海市青浦区2018届九年级数学上学期期末调研测试试题 沪科版
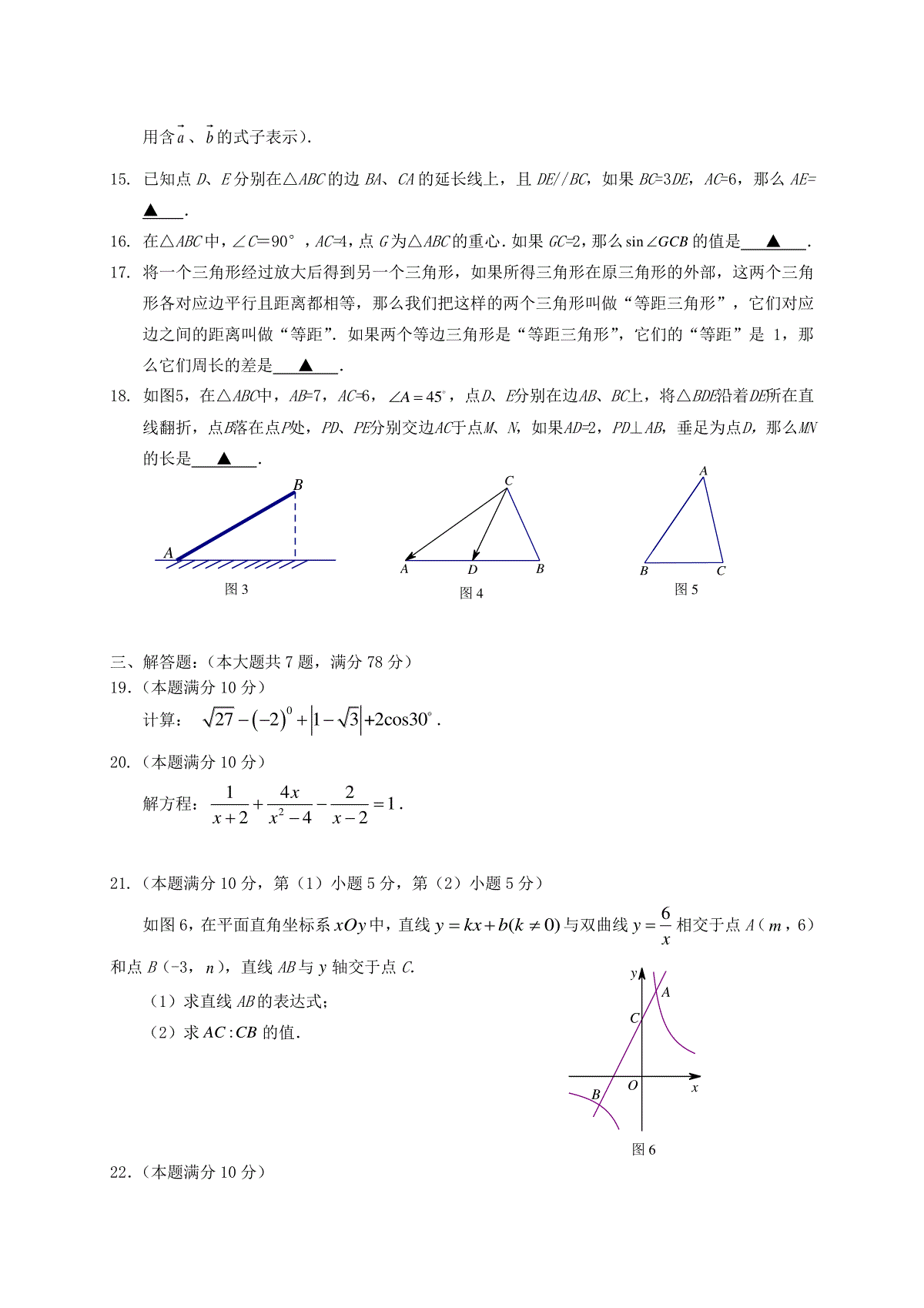
上海市青浦区2018届九年级数学上学期期末调研测试试题(完成时间:100分钟满分:150分)一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.计算32()x的结果是(▲)(A)5x;(B)5x;(C)6x;(D)6x.2.如果一次函数ykxb的图像经过一、二、三象限,那么k、b应满足的条件是(▲)(A)0k,且0b;(B)0k,且0b;(C)0k,且0b;(D)0k,且0b.3.下列各式中,2x的有理化因式是(▲)(A)2x;(B)2x;(C)2x;(D)2x.4.如图1,在△ABC中,∠ACB=90°,CD是AB边上的高.如果BD=4,CD=6,那么:BCAC是(▲)(A)3:2;(B)2:3;(C)3:13;(D)2:13.5.如图2,在□ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是(▲)(A)AECEEDEF;(B)AECDEDAF;(C)AEFAEDAB;(D)AEFEEDFC.6.在梯形ABCD中,AD//BC,下列条件中,不能判断梯形ABCD是等腰梯形的是(▲)(A)ABCDCB;(B)DBCACB;(C)DACDBC;(D)ACDDAC.二、填空题:(本大题共12题,每题4分,满分48分)7.因式分解:23aa▲.8.函数11yx的定义域是▲.9.如果关于x的一元二次方程2+20xxa没有实数根,那么a的取值范围是▲.10.抛物线24yx的对称轴是▲.11.将抛物线2yx平移,使它的顶点移到点P(-2,3),平移后新抛物线的表达式为▲.12.如果两个相似三角形周长的比是2:3,那么它们面积的比是▲.13.如图3,传送带和地面所成斜坡AB的坡度为1:3,把物体从地面A处送到坡顶B处时,物体所经过的路程是12米,此时物体离地面的高度是▲米.14.如图4,在△ABC中,点D是边AB的中点.如果CAa,CDb,那么CB▲(结果ABCDEF图2ABCD图1用含a、b的式子表示).15.已知点D、E分别在△ABC的边BA、CA的延长线上,且DE//BC,如果BC=3DE,AC=6,那么AE=▲.16.在△ABC中,∠C=90°,AC=4,点G为△ABC的重心.如果GC=2,那么sinGCB的值是▲.17.将一个三角形经过放大后得到另一个三角形,如果所得三角形在原三角形的外部,这两个三角形各对应边平行且距离都相等,那么我们把这样的两个三角形叫做“等距三角形”,它们对应边之间的距离叫做“等距”.如果两个等边三角形是“等距三角形”,它们的“等距”是1,那么它们周长的差是▲.18.如图5,在△ABC中,AB=7,AC=6,45A,点D、E分别在边AB、BC上,将△BDE沿着DE所在直线翻折,点B落在点P处,PD、PE分别交边AC于点M、N,如果AD=2,PD⊥AB,垂足为点D,那么MN的长是▲.三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:027213+2cos30.20.(本题满分10分)解方程:21421242xxxx.21.(本题满分10分,第(1)小题5分,第(2)小题5分)如图6,在平面直角坐标系xOy中,直线)0(kbkxy与双曲线xy6相交于点A(m,6)和点B(-3,n),直线AB与y轴交于点C.(1)求直线AB的表达式;(2)求:ACCB的值.22.(本题满分10分)BA图3DCBA图4图6xyOABCABC图5如图7,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD//AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43,顶部D的仰角是25,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)23.(本题满分12分,第(1)小题4分,第(2)小题8分)如图8,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCACECB.(1)求证:∠CAE=∠CBD;(2)若BEABECAC,求证:ABADAFAE.24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图9,在平面直角坐标系xOy中,抛物线20yaxbxca与x轴相交于点A(-1,0)和点B,与y轴交于点C,对称轴为直线1x.(1)求点C的坐标(用含a的代数式表示);(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)如图10,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.(1)当QD=QC时,求∠ABP的正切值;(2)设AP=x,CQ=y,求y关于x的函数解析式;ABCDEF图8CBAD图7图9CBAOyx(3)联结BQ,在△PBQ中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.图10QPDCBA备用图ABCD青浦区2017-2018学年第一学期九年级期末学业质量调研测试数学参考答案2018.1一、选择题:(本大题共6题,每题4分,满分24分)1.C;2.A;3.C;4.B;5.C;6.D.二.填空题:(本大题共12题,满分48分)7.31aa;8.1x;9.1a;10.直线0x或y轴;11.223yx;12.4:9;13.6;14.2ba;15.2;16.23;17.63;18.187.三、(本大题7题,第19~22题每题10分,第23、24题每题12分,第25题14分,满分78分)19.解:原式=321+31+223.…………………………………………………………(8分)=225.………………………………………………………………………(2分)20.解:方程两边同乘22xx得224224xxxx.…………………………(4分)整理,得2320xx.………………………………………………………………(2分)解这个方程得11x,22x.…………………………………………………………(2分)经检验,22x是增根,舍去.…………………………………………………………(1分)所以,原方程的根是1x.……………………………………………………………(1分)21.解:(1)∵点A(m,6)和点B(-3,n)在双曲线xy6,∴m=1,n=-2.∴点A(1,6),点B(-3,-2).………………………………………………………(2分)将点A、B代入直线ykxb,得=632.;kbkb解得=24.;kb…………………(2分)∴直线AB的表达式为:24yx.…………………………………………………(1分)(2)分别过点A、B作AM⊥y轴,BN⊥y轴,垂足分别为点M、N.……………………(1分)则∠AMO=∠BNO=90°,AM=1,BN=3,……………………………………………(1分)∴AM//BN,………………………………………………………………………………(1分)∴1=3ACAMCBBN.…………………………………………………………………………(2分)22.解:过点A作AE⊥CD,垂足为点E.……………………………………………………(1分)由题意得,AE=BC=28,∠EAD=25°,∠EAC=43°.………………………………(1分)在Rt△ADE中,∵tanDEEADAE,∴tan25280.472813.2DE.………(3分)在Rt△ACE中,∵tanCEEACAE,∴tan43280.932826CE.………(3分)∴13.22639DCDECE(米).………………………………………………(2分)答:建筑物CD的高度约为39米.23.(1)证明:∵CDCACECB,∴CECACDCB,………………………………………(1分)∵∠ECA=∠DCB,……………………………………………………………………(1分)∴△CAE∽△CBD,……………………………………………………………………(1分)∴∠CAE=∠CBD.……………………………………………………………………(1分)(2)证明:过点C作CG//AB,交AE的延长线于点G.∴BEABECCG,…………………………………………………………………………(1分)∵BEABECAC,∴ABABCGAC,……………………………………………………………(1分)∴CG=CA,……………………………………………………………………………(1分)∴∠G=∠CAG,………………………………………………………………………(1分)∵∠G=∠BAG,∴∠CAG=∠BAG.………………………………………………(1分)∵∠CAE=∠CBD,∠AFD=∠BFE,∴∠ADF=∠BEF.…………………………(1分)∴△ADF∽△AEB,……………………………………………………………………(1分)∴ADAFAEAB,∴ABADAFAE.…………………………………………………(1分)24.解:(1)∵抛物线20yaxbxca的对称轴为直线1x,∴12bxa,得2ba.…………………………………………………………(1分)把点A(-1,0)代入2yaxbxc,得=0abc,∴3ca.………………………………………………………………………………(1分)∴C(0,-3a).…………………………………………………………………………(1分)(2)∵点A、B关于直线1x对称,∴点B的坐标为(3,0).…………………………(1分)∴AB=4,OC=3a.…………………………………………………………………………(1分)∵12ABCSABOC,∴14362a,∴a=1,∴b=-2,c=-3,…………………………………………………………………(1分)∴223yxx.………………………………………………………………………(1分)(3)设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H.∵点G与点C,点F与点A关于点Q成中心对称,∴QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3,∴QF=m+1,QO=QH=m,OC=GH=3,∴OF=2m+1,HF=1.Ⅰ.当∠CGF=90°时,可得∠FGH=∠GQH=∠OQC,∴tantanFGHOQC,∴HFOCGHOQ,∴133m,∴=9m∴Q的坐标为(9,0).……………………………………………………………………(2分)Ⅱ.当∠CFG=90°时,可得,tantanFGHOFC,∴HFOCGHOF,∴13321m,∴=4m,Q的坐标为(4,0).……………………………………………………………(1分)Ⅲ.当∠GCF=90°时,∵∠GCF∠FCO90°,∴此种情况不存在.……………………………………………(1分)综上所述,点Q的坐标为(4,0)或(9,0).25.解:(1)延长PQ交BC延长线于点E.设PD=x.∵∠PBC=∠BPQ,∴EB=EP.…………………………………………………………………………………(1分)∵四边形A


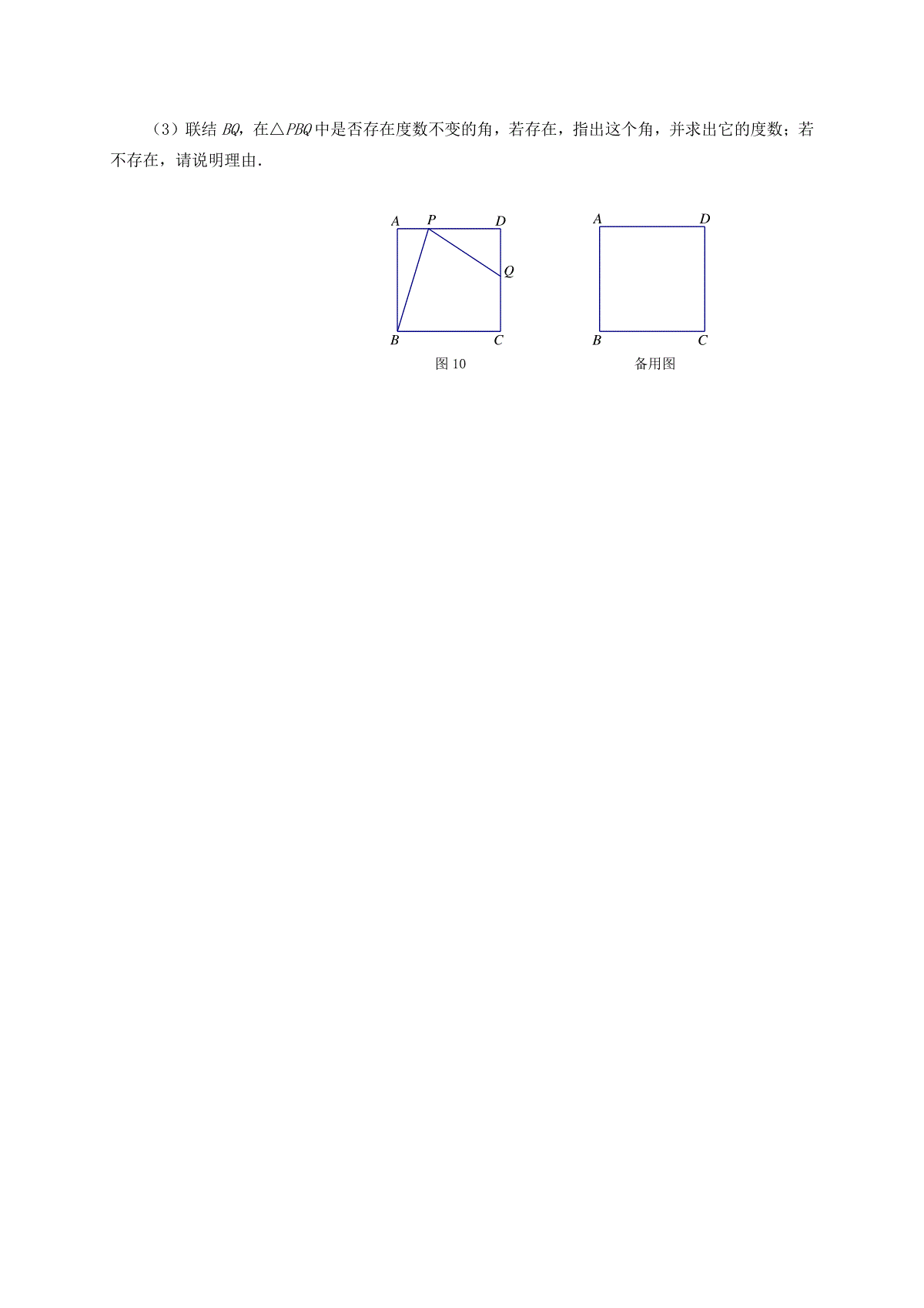

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 zcjy02938047
zcjy02938047
共134篇文档
格式: doc
大小: 259 KB
时间: 2021-04-13
本文标题:上海市青浦区2018届九年级数学上学期期末调研测试试题 沪科版
链接地址:https://www.777doc.com/doc-8031787 .html