九年级数学下册 第3章圆3.2点、直线与圆的位置关系 圆的切线3.2.3 三角形的内切圆教学课件 湘

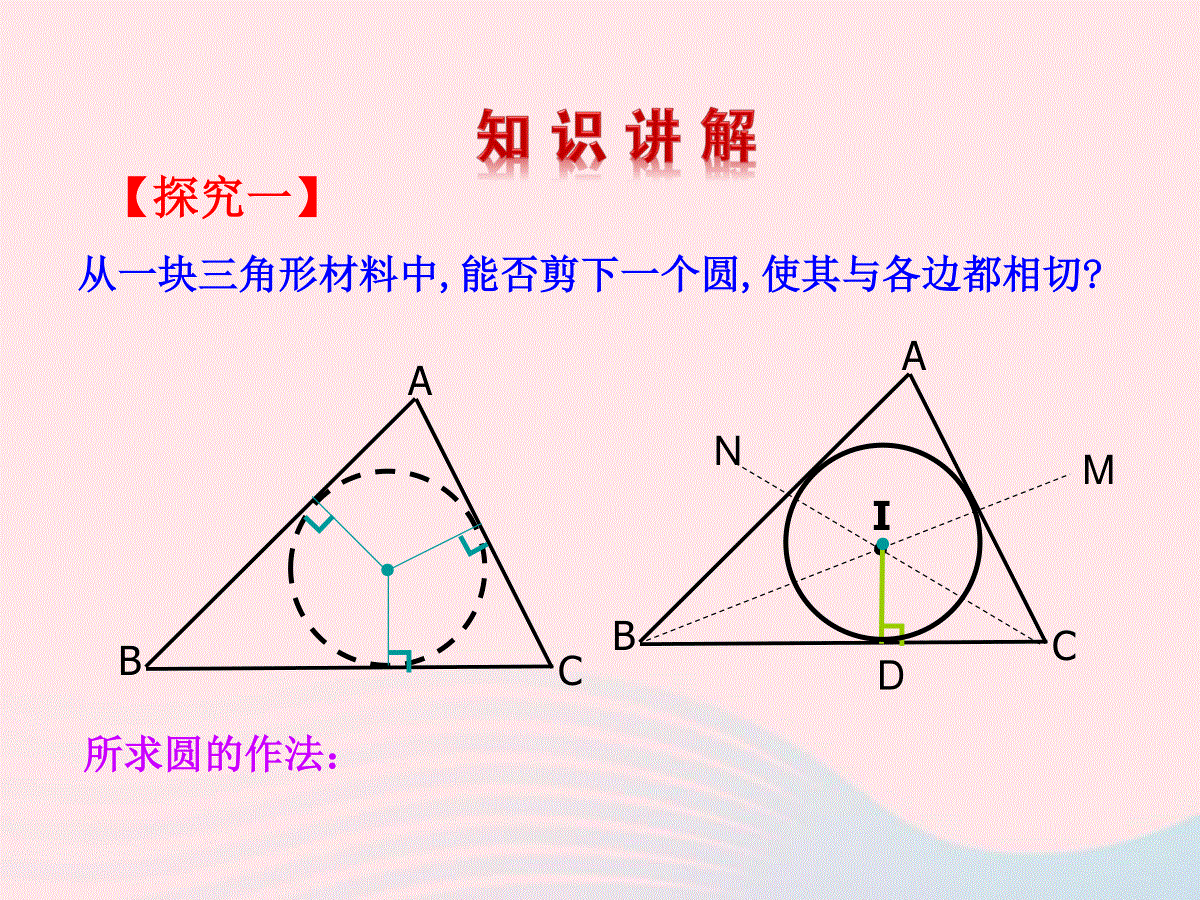
3.2.3三角形的内切圆1.使学生了解画三角形的内切圆的方法，了解三角形的内切圆、圆的外切三角形、三角形内心的概念.2.应用类比的数学思想方法研究内切圆，逐步培养学生的研究问题能力.3.激发学生动手、动脑主动参与课堂教学活动的热情．（2）直线l和⊙O相切（3）直线l和⊙O相交drd=rdrdorldorlodrl圆和直线的位置关系（1）直线l和⊙O相离从一块三角形材料中,能否剪下一个圆,使其与各边都相切?ABCABC●┓I●┓●所求圆的作法：DMN【探究一】（1）作∠ABC、∠ACB的平分线BM和CN，交点为I.（2）过点I作ID⊥BC，垂足为D.（3）以I为圆心，ID为半径作⊙I，则⊙I就是所求作的内切圆.∵直线BM和CN只有一个交点I,并且点I到△ABC三边的距离相等，因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.ABCI●┓●MN定义：与三角形各边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心叫做三角形的内心，是三角形三条角平分线的交点.这样的圆可以作出几个呢?为什么?分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明它们内心的位置情况.提示:先确定圆心和半径,尺规作图要保留作图痕迹.ABCABC●●●CAB┐【探究二】判断题：1.三角形的内心到三角形各个顶点的距离相等（）2.三角形的外心到三角形各边的距离相等（）3.等边三角形的内心和外心重合（）4.菱形一定有内切圆（）5.矩形一定有内切圆（）6.三角形的内心一定在三角形的内部（）错错对对错对【跟踪训练】例如图，在△ABC中，点O是内心，（1）若∠ABC=50°，∠ACB=70°，则∠BOC的度数为________（2）若∠A=80°，则∠BOC=_______（3）若∠BOC=110°，则∠A=______ABCO130°40°120°【例题】1.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,AC=3,BC=4.求⊙O的半径r.12543r.2cbar●ABCABC●O●┗┓ODEF直角三角形的三边长与其内切圆半径间的关系bac【跟踪训练】2.已知:如图,△ABC的面积S=4cm2,周长等于10cm.求内切圆⊙O的半径r.4rcm.5.2cbaSr1Srabc.2斜三角形的三边长及面积与其内切圆半径间的关系●●ABC●O┓EDF3.如图，某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑，以树立起文明古镇的形象.已知雕塑中心M到道路三边AC，BC，AB的距离相等，AC⊥BC，BC=30米，AC=40米.求镇标雕塑中心M离道路三边的距离有多远？ACB镇商业区镇工业区MEDFabc304050r10.22米提示：由AC⊥BC，BC=30米，AC=40米得AB=50米.所以答：中心M离道路三边的距离有10米远.1.（兰州·中考）如图，正三角形的内切圆半径为1，那么这个正三角形的边长为（）【答案】D3C．32D．A．2B．3ABC.oABCDEF2.设△ABC的边BC=8，AC=11，AB=15，内切圆I和BC，AC，AB分别相切于点D，E，F.求AE，CD，BF的长..Ixyz【解析】设AE=x，BF=y，CD=zxyz答：AE，CD，BF的长分别是9，2，6.x+y=15y+z=8x+z=11x=9y=6z=2则解得3.（黄冈·中考）如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，在AC延长线上有一点E，满足AD2＝AB·AE，求证：DE是⊙O的切线.ABCDE·O·P证明：连结DC，DO并延长交⊙O于F，连结AF.∵AD2＝AB·AE，∠BAD＝∠DAE，∴△BAD∽△DAE，∴∠ADB＝∠E.又∵∠ADB＝∠ACB，∴∠ACB＝∠E，BC∥DE，∴∠CDE＝∠BCD＝∠BAD＝∠DAC，又∵∠CAF＝∠CDF，∴∠FDE＝∠CDE+∠CDF＝∠DAC+∠CAF＝∠DAF＝90°，故DE是⊙O的切线.4.（衡阳·中考）如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，过点D的切线交BC于点E．（1）求证：12DEBC25（2）若tanC=，DE=2，求AD的长．【解析】(1)连结BD，∵AB为直径，∠ABC=90°，∴BE切⊙O于点B，因为DE切⊙O于点D，所以DE=BE，∴∠EBD=∠EDB，∵∠ADB=90°，∴∠EBD+∠C=90°，∠BDE+∠CDE=90°，∴∠C=∠EDC，∴DE=CE，BCDE211,2DEBC(2)因为DE=2，AB,BC所以BC=4，在Rt△ABC中，tanC=255,所以AB=BC·=2ACABABAD65252AD又因为△ABD∽△ACB，所以，即310所以AD=22BCAB在Rt△ABC中，AC=224)52(=6，本节课学习了以下内容：1．作三角形的内切圆．2．了解三角形的内切圆，三角形的内心概念．奔向理想人生的征途是漫长的，但是只要坚强不屈地向前奋进，理想就一定会实现.