当前位置:首页 > 中学教育 > 初中教育 > 中考数学 第二十讲 多边形与平行四边形复习课件
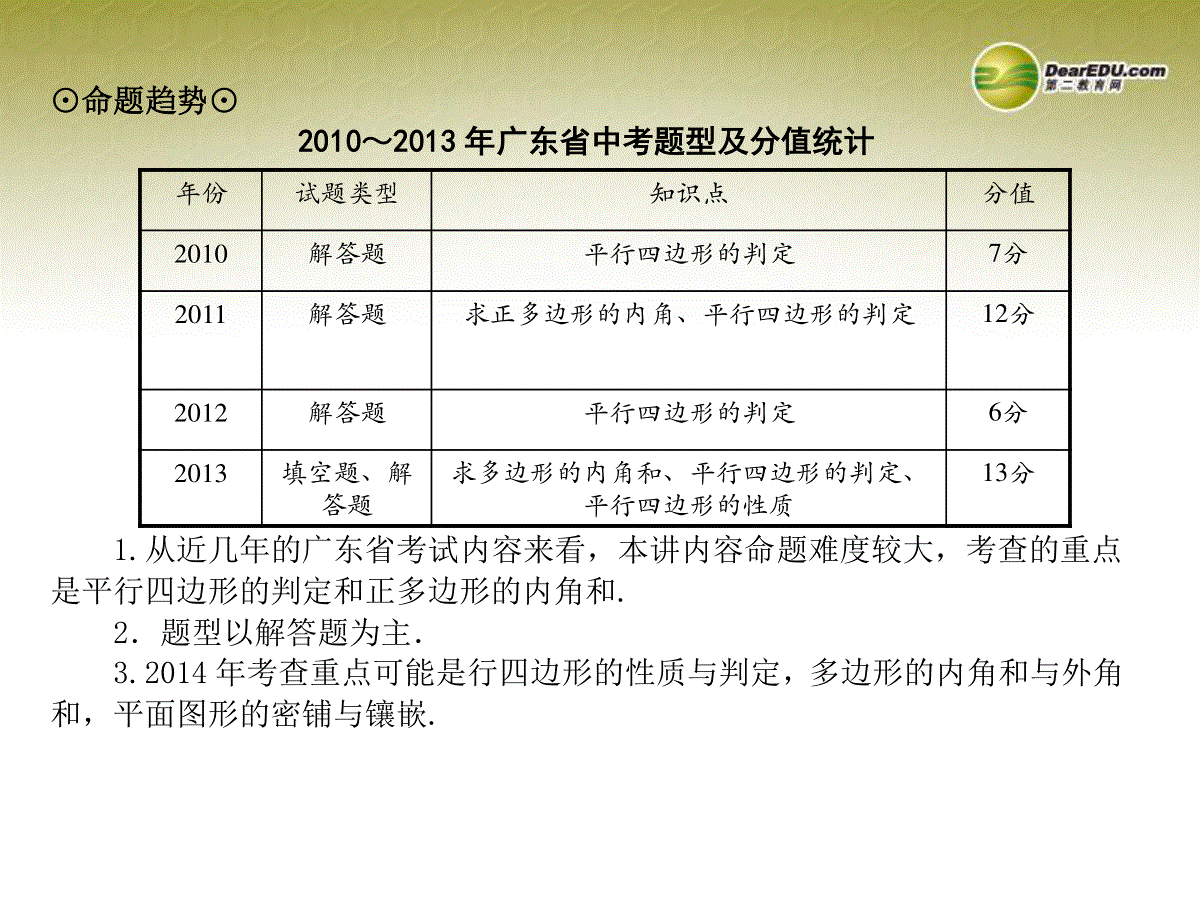
第二部分空间与代数第五章四边形第20讲多边形与平行四边形⊙考纲要求⊙1.了解多边形的内角和与外角和公式,了解正多边形的概念.2.掌握平行四边形的概念和性质,了解四边形的不稳定性.3.掌握平行四边形的有关性质和四边形是平行四边形的条件.4.了解平行四边形的重心及物理意义(如一根均匀木棒、一块均匀的矩形木板的重心).5.知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.★中考导航★⊙命题趋势⊙2010~2013年广东省中考题型及分值统计1.从近几年的广东省考试内容来看,本讲内容命题难度较大,考查的重点是平行四边形的判定和正多边形的内角和.2.题型以解答题为主.3.2014年考查重点可能是行四边形的性质与判定,多边形的内角和与外角和,平面图形的密铺与镶嵌.年份试题类型知识点分值2010解答题平行四边形的判定7分2011解答题求正多边形的内角、平行四边形的判定12分2012解答题平行四边形的判定6分2013填空题、解答题求多边形的内角和、平行四边形的判定、平行四边形的性质13分★课前预习★1.(2013湛江)已知一个多边形的内角和是540°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形2.四边形的内角和为,四边形的外角和为__________.3.(2013漳州)用下列一种多边形不能铺满地面的是()A.正方形B.正十边形C.正六边形D.等边三角形4.(2013广东)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是()A.30°B.40°C.50°D.60°5.(2013荆门)四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有()A.3种B.4种C.5种D.6种B360360BCB6.已知□ABCD的周长为32,AB=4,则BC=()A.4B.121C.24D.287.如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O.若AC=6,则线段AO的长度等于___________.B3★考点梳理★1.n边形的内角和为,外角和为.2.在平面内,各内角都相等,各边也都相等的多边形叫做正多边形.3.在多边形中,连结互不相邻两个顶点的线段叫做多边形的对角线.4.两组对边分别平行的四边形叫做平行四边形.5.平行四边形的性质:(1)平行四边形的分别平行;(2)平行四边形的分别相等;(3)平行四边形的分别相等;(4)平行四边形的对角线.6.平行四边形的判定:(1)两组对边的四边形是平行四边形.(2)一组对边的四边形是平行四边形.(3)两条对角线的四边形是平行四边形.7.当围绕一点拼在一起的几个多边形的内角和为360度时,可以镶嵌.8.同一种正多边形可以镶嵌的正多边形是正三角形、正方形和正六边形,两组对角互相平分两组对角分别相等平行且相等互相平分两组对边考点1.多边形的内角和与外角和、平面密铺与镶嵌(2010~2011、2013年考)1.(2013梅州)若一个多边形的内角和小于其外角和,则这个多边形的边数是()A.3B.4C.5D.6思路点拨:由于任何一个多边形的外角和为360°,由题意知此多边形的内角和小于360°.又根据多边形的内角和定理可知任何一个多边形的内角和必定是180°的整数倍,则此多边形的内角和等于180°.由此可以得出这个多边形的边数.★课堂精讲★A2.按下面摆好的方式,并使用同一种图形,只通过平移方式就能进行平面镶嵌(即平面密铺)的有(写出所有正确答案的序号).思路点拨:用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案.平面图形镶嵌的条件是:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成360°角.若能构成,则说明能够进行平面镶嵌;反之则不能.②③考点2.平行四边形性质(2009、2011~2013年考)3.(2013益阳)如图,在平行四边形ABCD中,下列结论中错误的是()A.∠1=∠2B.∠BAD=∠BCDC.AB=CDD.AC⊥BD思路点拨:根据平行四边形的性质,平行四边形对边平行以及对边相等和对角相等分别判断得出即可.D4.(2013攀枝花)如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.思路点拨:求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可.4.证明:∵BE=DF,∴BE-EF=DF-EF,∴DE=BF,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADE=∠CBF,在△ADE和△CBF中,BCADCBFADEBFDE∴△ADE≌△CBF(SAS),∴AE=CF.考点3.平行四边形判定(2009、2010、2012、2013年考)5.(2013郴州)如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.思路点拨:首先根据平行线的性质可得∠BEC=∠DFA,再加上条件∠ADF=∠CBE,AF=CE,可证明△ADF≌△CBE,再根据全等三角形的性质可得BE=DF,根据一组对边平行且相等的四边形是平行四边形进行判定即可.5.证明:∵BE∥DF,∴∠BEC=∠DFA,在△ADF和△CBE中,CEAFCEBAFDCBEADF∴△ADF≌△CBE(AAS),∴BE=DF,又∵BE∥DF,∴四边形DEBF是平行四边形.6.(2013龙岩)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.(1)求证:AE=CF;(2)求证:四边形EBFD是平行四边形.思路点拨:(1)通过全等三角形△ADE≌△CBF的对应边相等证得AE=CF;(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论.6.证明:(1)如图:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠3=∠4,∵∠1=∠3+∠5,∠2=∠4+∠6,∴∠1=∠2,∴∠5=∠6∵在△ADE与△CBF中,6543BCAD∴△ADE≌△CBF(ASA),∴AE=CF;(2)∵∠1=∠2,∴DE∥BF.又∵由(1)知△ADE≌△CBF,∴DE=BF,∴四边形EBFD是平行四边形.★随堂检测★1.(2013广东)一个六边形的内角和是.2.(2013呼和浩特)只用下列图形中的一种,能够进行平面镶嵌的是()A.正十边形B.正八边形C.正六边形D.正五边形3.(2013黔西南州)已知▱ABCD中,∠A+∠C=200°,则∠B的度数是()A.100°B.160°C.80°D.60°720°CC4.解:(1)如图:①作∠A′BD=∠ABD,②以B为圆心,AB长为半径画弧,交BA′于点A′,③连接BA′,DA′,则△A′BD即为所求;(2)∵四边形ABCD是平行四边形,∴AB=CD,∠BAD=∠C,由折叠的性质可得:∠BA′D=∠BAD,A′B=AB,∴∠BA′D=∠C,A′B=CD,在△BA′E和△DCE中,CDBADECBEACEBA,,,∴△BA′E≌△DCE(AAS).4.(2013广州)已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△A′BD.(1)利用尺规作出△A′BD.(要求保留作图痕迹,不写作法);(2)设DA′与BC交于点E,求证:△BA′E≌△DCE.5.(2013南平)如图,在▱ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.5.证明:在□ABCD中,AD=BC且AD∥BC∵BE=FD,∴AF=CE∴四边形AECF是平行四边形6.证明:(1)∵DF∥BE,∴∠DFE=∠BEF.又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS).(2)由(1)知△AFD≌△CEB,∴∠DAC=∠BCA,AD=BC,∴AD∥BC.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).6.(2013•鞍山)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.




 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:中考数学 第二十讲 多边形与平行四边形复习课件
链接地址:https://www.777doc.com/doc-3396836 .html