当前位置:首页 > 高等教育 > 研究生课件 > 9106年考研数四真题及答案解析
12006年全国硕士研究生入学考试数学(四)一、填空1.(1)1lim()nnnn2.设函数()fx在2x的某邻域内可导,且()()(2)1fxfxef,则法(2)f3.设函数()fu可微,且1()2fu,则22(4)zfxy在点(1,2)处的全微分(1,2)|dz4.已知12,aa为2维列向量,矩阵1212(2,)Aaaaa,12(,)Baa。若行列式||6A,则||B=5.设矩阵2112A,E为2阶单位矩阵,矩阵B满足2BABE,则B。6.设随机变量X与Y相互独立,且均服从区间[1,3]上的均匀分布,由{max(,)1}Pxy二、选择7.设函数()yfx具有二阶导数,且()0fx,()0fx,x为自变量x在点0x处的增量y与dy分别为()fx在点0x处对应的增量与微分,若0x,则()(A)0dyy(B)0ydy(C)0ydy(D)0dyy8.设函数()fx在0x处连续,且220()lim1nfnn,则()(A)(0)0f且(0)f存在(B)(0)1f且(0)f存在(C)(0)0f且(0)f存在(D)(0)1f且(0)f存在9.设函数()fx与()gx在[0,1]上连续,且()()fxgx,且对任何(0,1)C()(A)1122()()ccftdtgtdt(B)1122()()ccftdtgtdt2(C)11()()ccftdtgtdt(D)11()()ccftdtgtdt10.设非齐次线性微分方程()()yPxyQx有两个不同的解1()yx,2()yx,C为任何常数,则该方程通解是()(A)12[()()]Cyxyx(B)112()[()()]yxCyxyx(C)12[()()]Cyxyx(D)112()[()()]yxCyxyx11.设(,)fxy与(,)Gxy均为可微函数,且(,)0Gxy,已知00(,)xy是(,)fxy在约束条件(,)0Gxy下的一个极值点。下列选择正确的是()(A)若00(,)0xfxy,则00(,)0yfxy(B)若00(,)0xfxy,则00(,)0yfxy(C)若00(,)0xfxy,则00(,)0yfxy(D)若00(,)0xfxy,则00(,)0yfxy12.设A为3阶矩阵,将A的第2行加到第1行得B,再将B的第一列的-1倍加到第2列得C,记110010001P,则()(A)1CpAP(B)1CPAP(C)TCPAP(D)TCPAP13.设,AB为两个随机事件,且()0PB,(|)1PAB则有()(A)()()PABPA(B)()()PABPB(C)()()PABPA(C)()()PABPB14.设随机变量X服从正态分布211(,)Nu,随机变量Y服从正态分布222(,)Nu,且12{||13){||1)PXuPYu,则必有()(A)12(B)12(C)12uu(D)12uu三、解答题315.设1sin(,),0,01arctanxyyyfxyxyxyx求:(1)()lim(,)ygxfxy(2)0lim()ygx16.计算二重积分2Dyxydxdy,其中D是由曲线yx,1y,0x,所围成的平面区域。17.证明:当0ab时,sin2cossin2cosbbbbaaaa18.在xoy坐标平面中,连续曲线L过点(1,0)M,其上任意点(,)(0)Pxyx处的切线斜率与直线OP的斜率之差等于ax(常数0a)(1)求L的方程(2)当L与直线yax所围成平面图形的面积为时83,确定a的值。19.试确定常数,,ABC的值,使得23(1)1()xeBxCxAxOx,其中3()Ox是当0x时比3x高阶的无穷小。20.设4维向量组1(1,1,1,1)Taa,2(2,2,2,2)Taa,3(3,3,3,3)Taa,4(4,4,4,4)Taa,问a为何值时1234,,,aaaa线性相关?当1234aaaa线性相关时,求其一个极大线性无关组,并将其余量用该极大线性无关组线性表出。21.设3阶实对称矩阵A的各行元素之和均为3,向量1(1,2,1)TI,2(0,1,1)TI,是线性方程组0Ax的两个解。(1)求A的特征值与特征向量(2)求正交矩阵Q和对角矩阵A,使TQAQA;(3)求A及3()2AE,其中E为3阶单位矩阵。22.设二维随机变量(,XY)的概率分布为其中,,abc为常数,且x的数学期望0.2EX,{0,0}0.5Pxy,记ZXY求:(1),,abc的值(2)Z的概率分布(3){}PXZ23.设随机变量X的概率密度为41,1021(),02,40,yxfxx其它令2YX,(,)FXY为二维随机变量(,)XY的分布函数。求:(1)Y的概率密度()Yfy(2)cov(,)XY(3)1(,4)2F5题解678910111213线代(4)设1,2是两个2维向量,A=(21+2,1-2),B=(1,2).已知|A|=6,则|B|=().解:可以用行列式的性质解,但是用新东方辅导班上介绍的“矩真分解法”来做更加简单:A=(21+2,1-2)=(1,2)21=B21,1-11-1两边取行列式,得6=-3|B|,|B|=-2.(5)设A=21,2阶矩阵B满足BA=B+2E,则B=.-12解:由BA=B+2E化得B(A-E)=2E,于是B=2(A-E)-1=|A-E|(A-E)-1(|A-E|=2)=(A-E)*=1-1.11(12)设A是3阶矩阵,将A的第2列加到第1列上得B,将B的第1列的-1倍加到第2列上得C.记110P=010,则001(A)C=P-1AP.(B)C=PAP-1.(C)C=PTAP.(D)C=PAPT.解:(B)用初等矩阵在乘法中的作用得出B=PA,1-10C=B010=BP-1=PAP-1.001(20)设1=(1+a,1,1,1),2=(2,2+a,2,2),3=(3,3+a,3,3),4=(4,4,4,4+a).问a为什么数时1,2,3,4线性相关?在时1,2,3,4线性相关时求其一个极大线性无关组,并且把其余向量用该极大线性无关组线性表出.解:1,2,3,4线性相关,即行列式|1,2,3,4|=0,而|1,2,3,4|=a3(a+10),于是当a=0或-10时1,2,3,4线性相关.a=0时,1是1,2,3,4的极大无关组,2=21,3=31,4=41.a=-10时,-9234-100010100-1(1,2,3,4)=1-8340-10010010-1.12-7400-1010001-1123–6123-60000则1,2,3是1,2,3,4的极大无关组,4=-1-2-3.(21)设3阶实对称矩阵A的各行元素之和都为3,向量1=(-1,2,-1)T,2=(0,-1,1)T都是齐次线性方程组AX=0的解.①求A的特征值和特征向量.14②求作正交矩阵Q和对角矩阵,使得QTAQ=.③求A及[A-(3/2)E]6.解:①条件说明A(1,1,1)T=(3,3,3)T,即0=(1,1,1)T是A的特征向量,特征值为3.又1,2都是AX=0的解说明它们也都是A的特征向量,特征值为0.由于1,2线性无关,特征值0的重数大于1.于是A的特征值为3,0,0.属于3的特征向量:c0,c0.属于0的特征向量:c11+c22,c1,c2不都为0.②将0单位化,得0=(33,33,33)T.对1,2作施密特正交化,的1=(0,-22,22)T,2=(-36,66,66)T.作Q=(0,1,2),则Q是正交矩阵,并且300QTAQ=Q-1AQ=000.000③1-10300111A1-2-1=300,解此矩阵方程,得A=111.1-11300111(A-23E)2=A2-3A+49E=49E,(A-23E)6=64729E.15概率(6)91(13)C(14)A(22)解:(Ⅰ)X的边缘分布为X-101Pa+0.2b+0.3c+0.12.0)1.0()2.0()(caXE5.05.01.0}0{}0,0{}0/0{babaXPYXPXYP11.01.02.02.0cba所以:1.0,1.0,2.0cba(Ⅱ)Z-2-1012P0.20.10.30.30.1(Ⅲ)2.01.01.00}0{}{YPZXP(23)随机变量X的概率密度为其他,020,4101,21)(xxxfX,令2XY,),(yxF为二维随机变量)(YX,的分布函数。(Ⅰ)求Y的概率密度;(Ⅱ)),cov(YX;(Ⅲ))4,21(F解:(Ⅰ)yyyyyXPyYPyFY4,141,)2(10,)1(0,0)()()(2式式yyydxdxyXyP00434121)()1(式;16yydxdxyXyP00141214121)()2(式。所以:其他,041,8110,83)()('yyyyyFyfYY这个解法是从分布函数的最基本的概率定义入手,对y进行适当的讨论即可,在新东方的辅导班里我也经常讲到,是基本题型。(Ⅱ)),cov(YX)()()()()()(23XEXEXEYEXEXYE2001414121)(dxxdxxXE;2020122654121)(dxxdxxXE;2030133874121)(dxxdxxXE所以:),cov(YX32654187。(Ⅲ))4,21(F)212()22,21()4,21()4,21(2XPXXPXXPYXP4121211dx。(23)设总体X的概率密度为其他,021,110,),(xxxf,其中是未知参数(01)。nXXX,,21为来自总体的简单随机样本,记N为样本值nxxx,,21中小于1的个数。求:(Ⅰ)的矩估计;(Ⅱ)的最大似然估计。17解:(Ⅰ)23)1()(2110dxxdxxXEX,所以:X23矩。(Ⅱ)对样本nxxx,,21按照1或者≥1进行分类:pNppxxx,,211,pnpNpNxxx,,21≥1。似然函数其他,,01,,,1,,)1()(2121pnpNpNpNppNnNxxxxxxL,在pNppxxx,,211,pnpNpNxxx,,21≥1时,)1ln()(ln)(lnNnNL,01)(lnNnNdLd,所以nN最大。181920



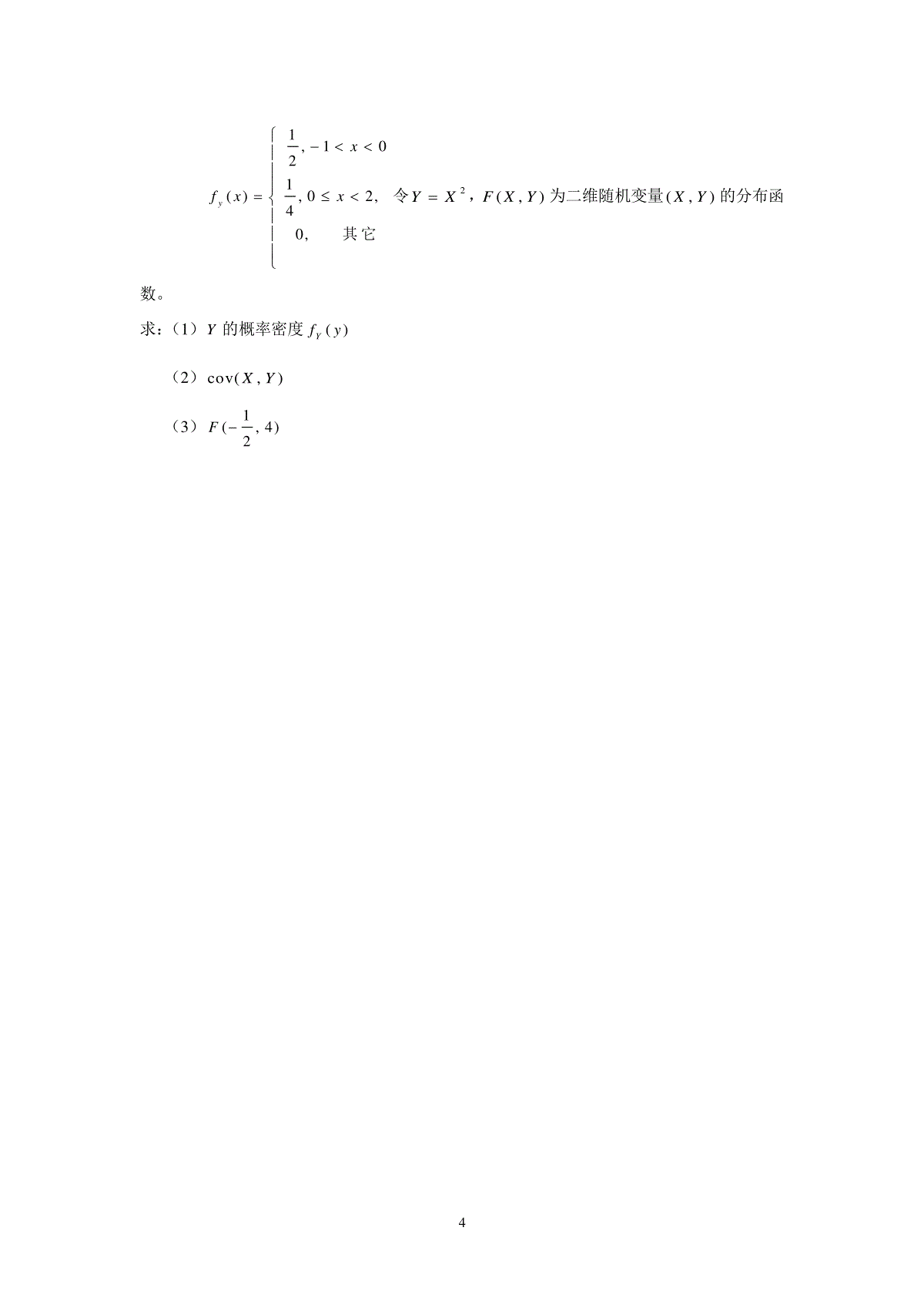

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:9106年考研数四真题及答案解析
链接地址:https://www.777doc.com/doc-4283242 .html