中考数学 辅助线

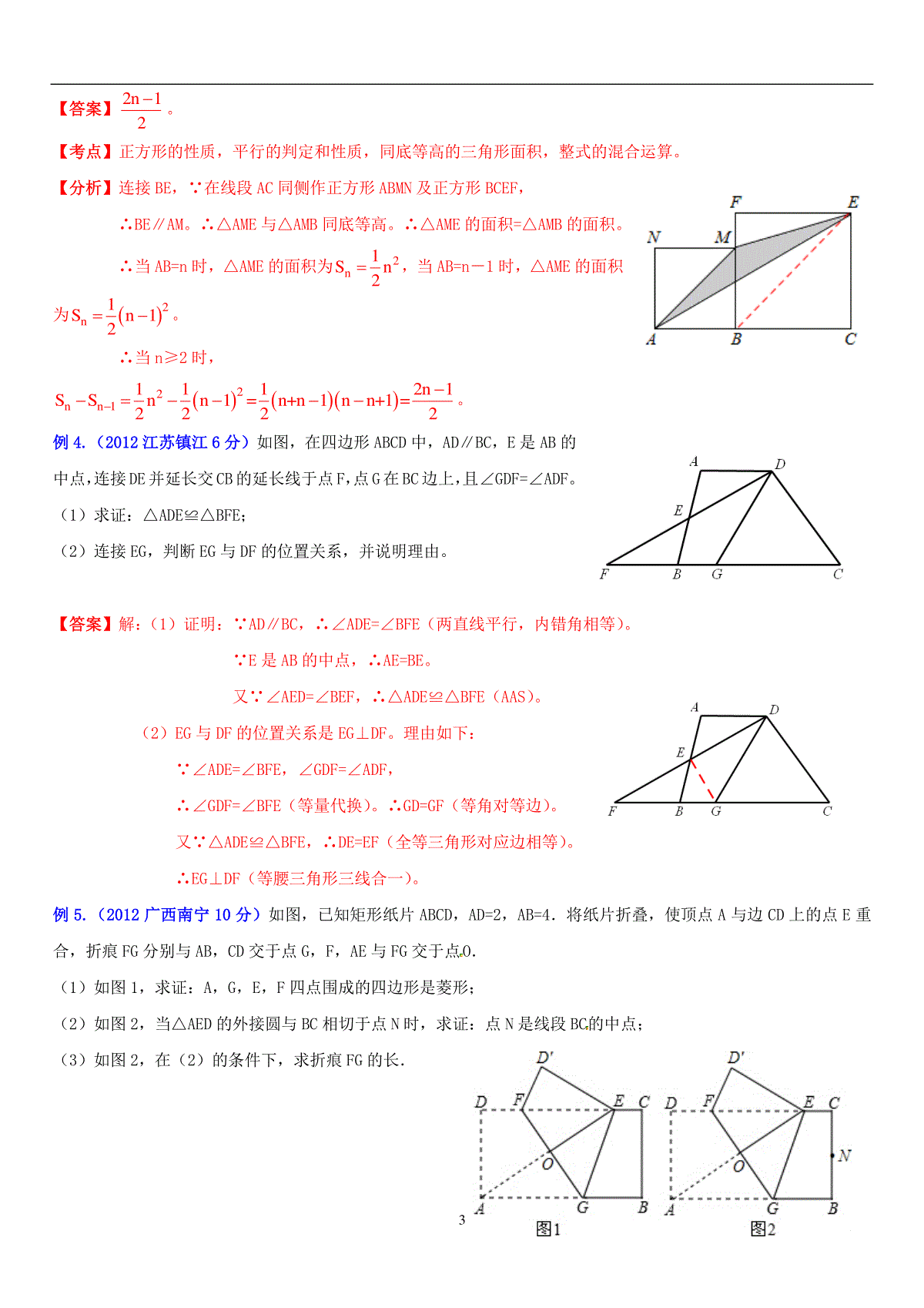
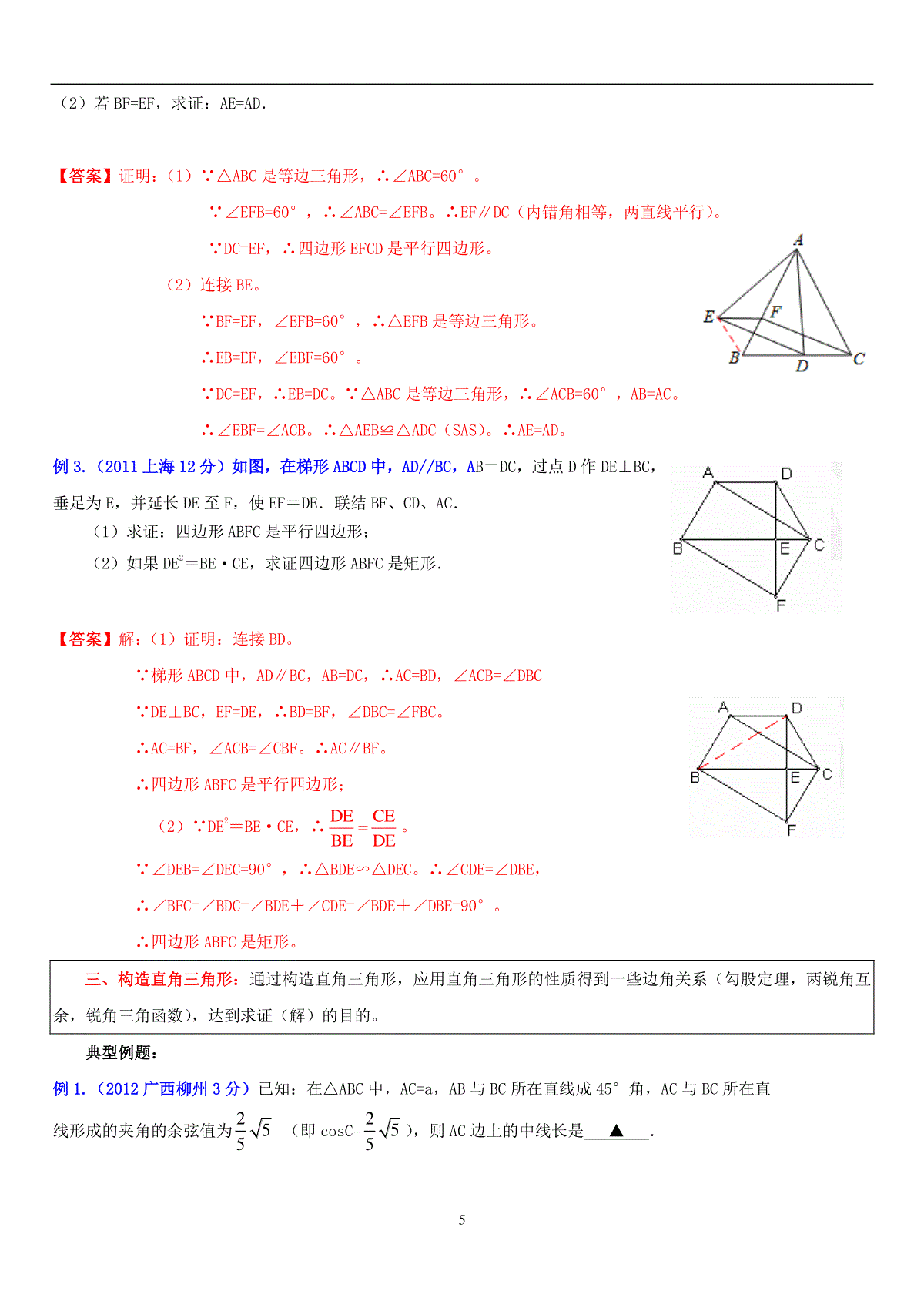
1几何辅助线（图）作法探讨一些几何题的证明或求解，由原图形分析探究，有时显得十分复杂，若通过适当的变换，即添加适当的辅助线（图），将原图形转换成一个完整的、特殊的、简单的新图形，则能使原问题的本质得到充分的显示，通过对新图形的分析，原问题顺利获解。有许多初中几何常见辅助线作法歌诀，下面这一套是很好的：人说几何很困难，难点就在辅助线。辅助线，如何添？把握定理和概念。还要刻苦加钻研，找出规律凭经验。三角形图中有角平分线，可向两边作垂线。也可将图对折看，对称以后关系现。角平分线平行线，等腰三角形来添。角平分线加垂线，三线合一试试看。线段垂直平分线，常向两端把线连。要证线段倍与半，延长缩短可试验。三角形中两中点，连接则成中位线。三角形中有中线，延长中线等中线。四边形平行四边形出现，对称中心等分点。梯形里面作高线，平移一腰试试看。平行移动对角线，补成三角形常见。证相似，比线段，添线平行成习惯。等积式子比例换，寻找线段很关键。直接证明有困难，等量代换少麻烦。斜边上面作高线，比例中项一大片。圆半径与弦长计算，弦心距来中间站。圆上若有一切线，切点圆心半径连。切线长度的计算，勾股定理最方便。要想证明是切线，半径垂线仔细辨。是直径，成半圆，想成直角径连弦。弧有中点圆心连，垂径定理要记全。圆周角边两条弦，直径和弦端点连。弦切角边切线弦，同弧对角等找完。要想作个外接圆，各边作出中垂线。还要作个内切圆，内角平分线梦圆。如果遇到相交圆，不要忘作公共弦。内外相切的两圆，经过切点公切线。若是添上连心线，切点肯定在上面。要作等角添个圆，证明题目少困难。辅助线，是虚线，画图注意勿改变。假如图形较分散，对称旋转去实验。基本作图很关键，平时掌握要熟练。解题还要多心眼，经常总结方法显。切勿盲目乱添线，方法灵活应多变。分析综合方法选，困难再多也会减。虚心勤学加苦练，成绩上升成直线。2在几何题的证明或求解时，需要构成一些基本图形来求证（解）时往往要通过添加辅助线（图）来形成，添加辅助线（图），构成的基本图形是结果，构造的手段是方法。笔者从作辅助线的结果和方法两方面将几何辅助线（图）作法归纳为结果―――（1）构造基本图形；（2）构造等腰（边）三角形：（3）构造直角三角形；（4）构造全等三角形；（5）构造相似三角形；（6）构造特殊四边形；（7）构造圆的特殊图形；方法―――（8）基本辅助线；（9）截取和延长变换；（10）对称变换；（11）平移变换；（12）旋转变换。下面通过近年全国各地中考的实例探讨其应用。一、构造基本图形：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形。如平行线，垂直线，直角三角形斜边上中线，三角形、四边形的中位线等。等腰（边）三角形、直角三角形、全等三角形、相似三角形、特殊四边形和圆的特殊图形也都是基本图形，但我们后面把它们单独表述。典型例题：例1.（2012四川内江3分）如图，3,1402,651,//00则ba【】A.0100B.0105C.0110D.0115例2.（2012江苏宿迁3分）已知点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，若AC⊥BD，且AC≠BD，则四边形EFGH的形状是▲.（填“梯形”“矩形”“菱形”）【答案】矩形。【考点】三角形中位线定理，矩形的判定。【分析】如图，连接AC，BD。∵E，F，G，H分别是AB，BC，CD，DA的中点，∴根据三角形中位线定理，HE∥AB∥GF，HG∥AC∥EF。又∵AC⊥BD，∴∠EHG=∠HGF=∠GFE=∠FEH=900。∴四边形EFGH是矩形。且∵AC≠BD，∴四边形EFGH邻边不相等。∴四边形EFGH不可能是菱形。例3.（2012湖北天门、仙桃、潜江、江汉油田3分）如图，线段AC=n+1（其中n为正整数），点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME．当AB=1时，△AME的面积记为S1；当AB=2时，△AME的面积记为S2；当AB=3时，△AME的面积记为S3；…；当AB=n时，△AME的面积记为Sn．当n≥2时，Sn﹣Sn﹣1=▲．3【答案】2n12。【考点】正方形的性质，平行的判定和性质，同底等高的三角形面积，整式的混合运算。【分析】连接BE，∵在线段AC同侧作正方形ABMN及正方形BCEF，∴BE∥AM。∴△AME与△AMB同底等高。∴△AME的面积=△AMB的面积。∴当AB=n时，△AME的面积为2n1Sn2，当AB=n－1时，△AME的面积为2n1Sn12。∴当n≥2时，22nn11112n1SSnn1=n+n1nn+1=2222。例4.（2012江苏镇江6分）如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在BC边上，且∠GDF=∠ADF。（1）求证：△ADE≌△BFE；（2）连接EG，判断EG与DF的位置关系，并说明理由。【答案】解：（1）证明：∵AD∥BC，∴∠ADE=∠BFE（两直线平行，内错角相等）。∵E是AB的中点，∴AE=BE。又∵∠AED=∠BEF，∴△ADE≌△BFE（AAS）。（2）EG与DF的位置关系是EG⊥DF。理由如下：∵∠ADE=∠BFE，∠GDF=∠ADF，∴∠GDF=∠BFE（等量代换）。∴GD=GF（等角对等边）。又∵△ADE≌△BFE，∴DE=EF（全等三角形对应边相等）。∴EG⊥DF（等腰三角形三线合一）。例5.（2012广西南宁10分）如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC的中点；（3）如图2，在（2）的条件下，求折痕FG的长．4【答案】解：（1）由折叠的性质可得，GA=GE，∠AGF=∠EGF，∵DC∥AB，∴∠EFG=∠AGF。∴∠EFG=∠EGF。∴EF=EG=AG。∴四边形AGEF是平行四边形（EF∥AG，EF=AG）。又∵AG=GE，∴四边形AGEF是菱形。（2）连接ON，∵△AED是直角三角形，AE是斜边，点O是AE的中点，△AED的外接圆与BC相切于点N，∴ON⊥BC。∵点O是AE的中点，∴ON是梯形ABCE的中位线。∴点N是线段BC的中点。（3）∵OE、ON均是△AED的外接圆的半径，∴OE=OA=ON=2。∴AE=AB=4。在Rt△ADE中，AD=2，AE=4，∴∠AED=30°。在Rt△OEF中，OE=2，∠AED=30°，∴23OF3。∴FG=432OF3。二、构造等腰（边）三角形：当问题中出现一点发出的二条相等线段时往往要补完整等腰（边）三角形；出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰（边）三角形。通过构造等腰（边）三角形，应用等腰（边）三角形的性质得到一些边角相等关系，达到求证（解）的目的。典型例题：例1.（2012浙江丽水、金华4分）如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是▲．【答案】50°。连接BO，∵AB＝AC，AO是∠BAC的平分线，∴AO是BC的中垂线。∴BO＝CO。∵∠BAC＝50°，∠BAC的平分线与AB的中垂线交于点O，∴∠OAB＝∠OAC＝25°。∵等腰△ABC中，AB＝AC，∠BAC＝50°，∴∠ABC＝∠ACB＝65°。∴∠OBC＝65°－25°＝40°。∴∠OBC＝∠OCB＝40°。∵点C沿EF折叠后与点O重合，∴EO＝EC，∠CEF＝∠FEO。∴∠CEF＝∠FEO＝（1800－2×400）÷2＝50°。例2.（2012甘肃白银10分）如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°，DC=EF．（1）求证：四边形EFCD是平行四边形；5（2）若BF=EF，求证：AE=AD．【答案】证明：（1）∵△ABC是等边三角形，∴∠ABC=60°。∵∠EFB=60°，∴∠ABC=∠EFB。∴EF∥DC（内错角相等，两直线平行）。∵DC=EF，∴四边形EFCD是平行四边形。（2）连接BE。∵BF=EF，∠EFB=60°，∴△EFB是等边三角形。∴EB=EF，∠EBF=60°。∵DC=EF，∴EB=DC。∵△ABC是等边三角形，∴∠ACB=60°，AB=AC。∴∠EBF=∠ACB。∴△AEB≌△ADC（SAS）。∴AE=AD。例3.（2011上海12分）如图，在梯形ABCD中，AD//BC，AB＝DC，过点D作DE⊥BC，垂足为E，并延长DE至F，使EF＝DE．联结BF、CD、AC．（1）求证：四边形ABFC是平行四边形；（2）如果DE2＝BE·CE，求证四边形ABFC是矩形．【答案】解：（1）证明：连接BD。∵梯形ABCD中，AD∥BC，AB=DC，∴AC=BD，∠ACB=∠DBC∵DE⊥BC，EF=DE，∴BD=BF，∠DBC=∠FBC。∴AC=BF，∠ACB=∠CBF。∴AC∥BF。∴四边形ABFC是平行四边形；（2）∵DE2＝BE·CE，∴DECEBEDE。∵∠DEB=∠DEC=90°，∴△BDE∽△DEC。∴∠CDE=∠DBE，∴∠BFC=∠BDC=∠BDE＋∠CDE=∠BDE＋∠DBE=90°。∴四边形ABFC是矩形。三、构造直角三角形：通过构造直角三角形，应用直角三角形的性质得到一些边角关系（勾股定理，两锐角互余，锐角三角函数），达到求证（解）的目的。典型例题：例1.（2012广西柳州3分）已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的夹角的余弦值为255（即cosC=255），则AC边上的中线长是▲．6【答案】85a10或510a。【分析】分两种情况：①△ABC为锐角三角形时，如图1，BE为AC边的中线。作△ABC的高AD，过点E作EF⊥BC于点F。∵在Rt△ACD中，AC=a，cosC=255，∴CD=255a，AD=55a。∵在Rt△ABD中，∠ABD=45°，∴BD=AD=55a。。∴BC=BD+CD=355a。∵点E是AC的中点，EF∥AD，∴EF是△ACD的中位线。∴FC=12DC=55a，EF=12AD=510a。∴BF=255a。在Rt△BEF中，由勾股定理，得22222251785BEBFEF5aa=a=a5102010。②△ABC为钝角三角形时，如图2，BE为AC边的中线。作△ABC的高AD。∵在Rt△ACD中，AC=a，cosC=255，∴CD=255a，AD=55a。∵在Rt△ABD中，∠ABD=45°，∴BD=AD=55a。∴BC=BD=55a。∵点E是AC的中点，∴BE是△ACD的中位线。∴BE=12AD=510a。综上所述，AC边上的中线长是85a10或510a。例2.（2012广西河池3分）如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连结CN．若△CDN的面积与△CMN的面积比为1︰4，则MNBM的值为【】7A．2B．4C．25D．26【答案】D。过点N作NG⊥BC于G，∵四边形ABCD是矩形，∴四边形CDNG是矩形，AD∥BC。∴CD=NG，CG=DN，∠ANM=∠CMN。由折叠的性质可得：AM=CM，∠AMN=∠CMN，∴∠ANM=∠AMN。∴AM=AN。∴AM=CM，∴四边形AMCN是平行四边形。∵AM=CM，∴四边形AMCN是菱形。∵△CDN的面积与△CMN的面积比为1：4，∴DN：CM=1：4。设DN=x，则AN=AM=CM=CN=4x，AD=BC=5x，CG=x。∴BM=x，GM=3x。在Rt△CGN中，2222NGCNCG4xx15x，在Rt△MNG中，22