浙教版八年级数学下册期中试卷

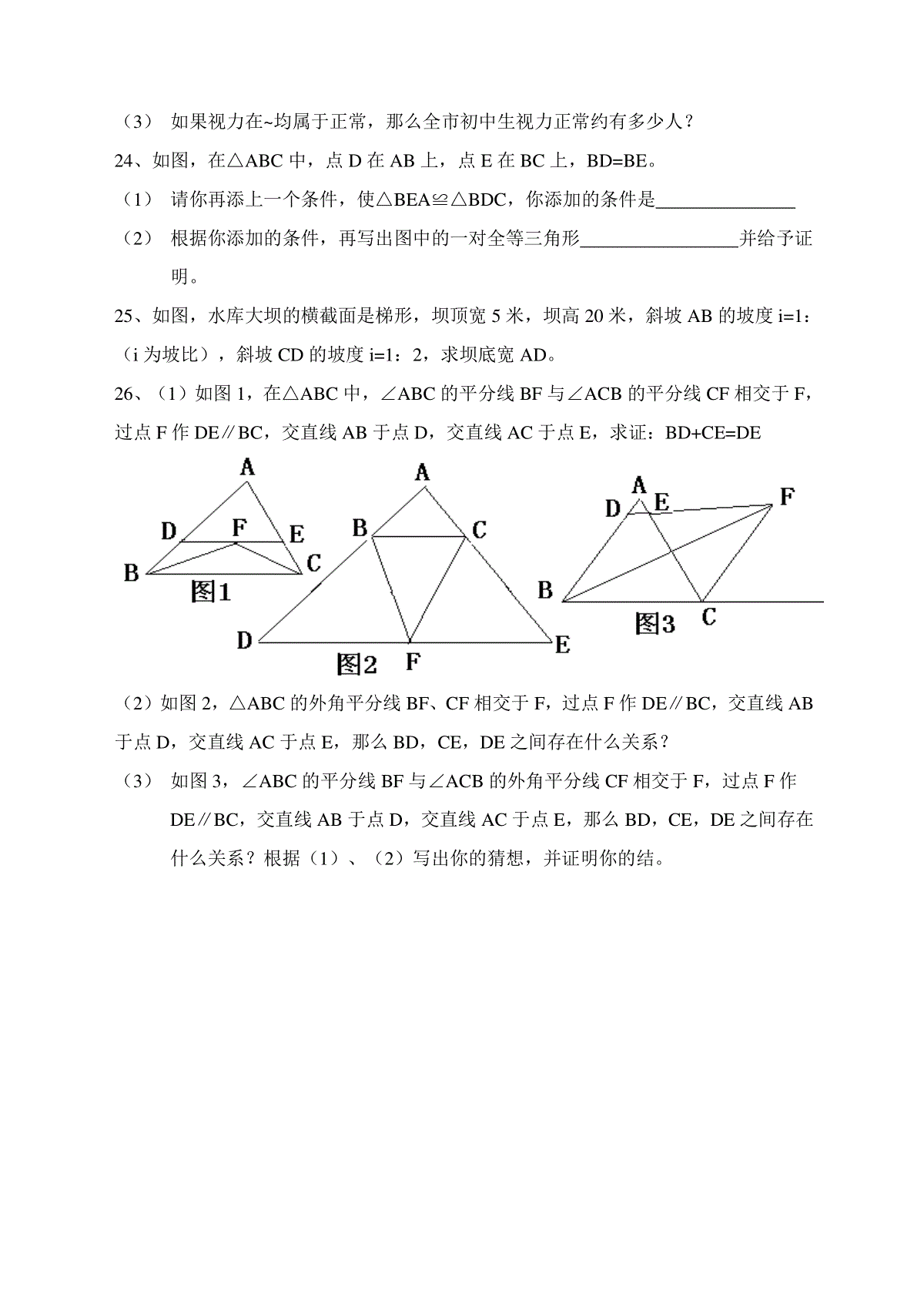
班级________姓名________一、填空题(每小题3分，共30分)1、方程3x2=x的解是2、在平面直角坐标系中点A57，到原点的距离是3、如果x2-3ax+9是一个完全平方式，则a=4、写出命题“对顶角相等”的题设5、将50个数据分成5组列出频数分布表，其中第一组的频数为6，第二组与第五组的频数和为20，第三组的频率为，则第四组的频数为6、公司1996年出口创汇135万美元，1997、1998年每年比上一年增加a%，那么1998年这个公司出口创汇美元。7、已知2324550abc则一元二次方程ax2+bx+c=0的根的情况是8、在一条线段上取n个点，过n个点连同线段的两个端点一共有（n+2）个点，若以这（n+2）个点中任意两点为端点的线段有45条，则n=9、已知a=52，b=52，则227ab=10、如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC则∠ABC=度。二、选择题(每小题3分，共30分)11、对于任意实数，代数式x2-6x+10的值是一个（）A、非负数B、正数C、负数D、整数12、关于x的一元二次方程x2+3kx+k2-1=0的根的情况是（）A、有两个不相等的实数根B、有两个相等的实数根C、没有实数根D、无法确定13、若0aa则221aa等于（）A、1-2aB、2a-1C、-1D、114、若关于x的一元二次方程22a-1x+x+a-1=0的一个根是0，则a的值是（）A、1B、-1C、1或-1D、1215、两个正方形，小正方形的边长比大正方形的边长的一半多4cm，大正方形的面积比小正方形的面积的2倍少32cm2，则大、小两个正方形的边长依次是（）A、18cm和10cmB、17cm和11cmC、16cm和12cmD、15cm和13cm16、如果22121aabbab，则a与b的关系是（）A、a≦bB、a＜bC、a≧bD、a＞b17、在三角形纸片ABC中，∠A=65°，∠B=75°将纸片的一角对折，使点C落在△ABC内，若∠1=20°，则∠2的度数为（）A、50°B、60°C、70°D、80°18、如果一个三角形的三边长分别为1，k，3化简274368123kkk的结果是（）A、-5B、1C、13D、19-4k19、下面说法中正确的是（）A、“同位角相等”的题设是“两个角相等”B、因为“相等的角是对顶角”是假命题，所以它没有题设。C、如果ab=0，那么a+b=0是真命题。D、用反证法证明命题“如果a∥b，a∥c那么b∥c时，第一步应假设b与c不平行。20、如果代数式232xx的值为9，则代数式5932xx的值为（）A．16B．16C．0D．4三、解答题21、计算（4分）22、解方程（每小题4分，共8分）①229121xx②2260xx23、中学生与小学生的视力状况受到全社会的广泛关注，某市部门对全市4万名初中生的视力状况进行一次抽样调查统计，所得到的有关数据绘制成频数分布直方图，如图，从左到右五个小组的频率之比依次是2：4：9：7：3，第五小组频数是30。（1）样本容量是多少？（2）中位数应在哪一组？新课标第一网（3）如果视力在~均属于正常，那么全市初中生视力正常约有多少人？24、如图，在△ABC中，点D在AB上，点E在BC上，BD=BE。（1）请你再添上一个条件，使△BEA≌△BDC，你添加的条件是（2）根据你添加的条件，再写出图中的一对全等三角形并给予证明。25、如图，水库大坝的横截面是梯形，坝顶宽5米，坝高20米，斜坡AB的坡度i=1：（i为坡比），斜坡CD的坡度i=1：2，求坝底宽AD。26、（1）如图1，在△ABC中，∠ABC的平分线BF与∠ACB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，求证：BD+CE=DE（2）如图2，△ABC的外角平分线BF、CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，那么BD，CE，DE之间存在什么关系？（3）如图3，∠ABC的平分线BF与∠ACB的外角平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E，那么BD，CE，DE之间存在什么关系？根据（1）、（2）写出你的猜想，并证明你的结。