北师版高中数学必修一第12讲：幂函数（学生版）

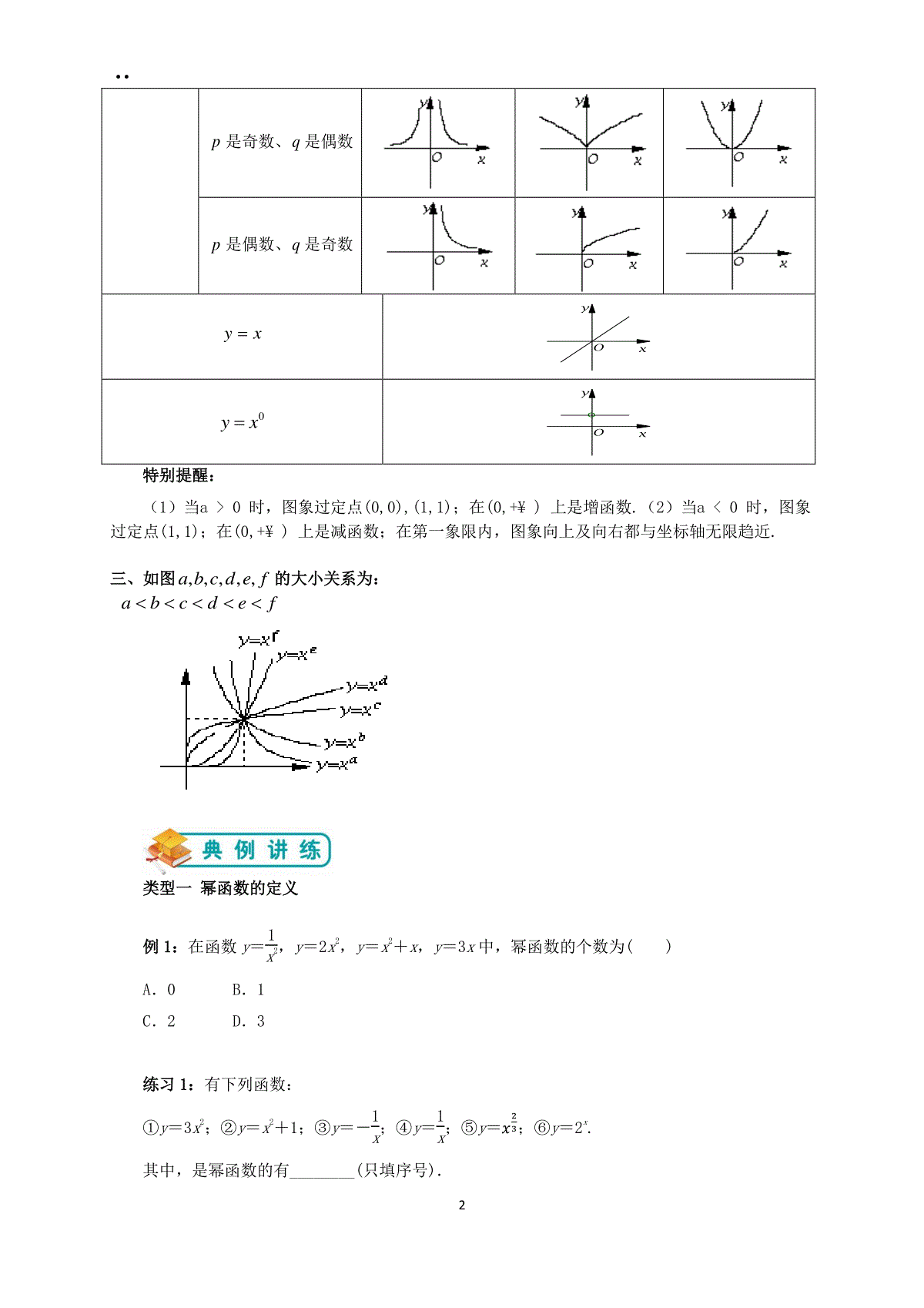
··1幂函数____________________________________________________________________________________________________________________________________________________________________1、通过实例，了解幂函数的概念；结合函数y=x，y=，y=，y=，的图像，了解它们的变化情况.2、通过对幂函数的研究，加深对函数概念的理解.一、定义：一般地，我们把形如ayxaR的函数叫做幂函数，其中a为常数。特别提醒：幂函数的基本形式是y=，其中x是自变量，a是常数.要求掌握y=x，y=，y=，y=，y=这五个常用幂函数的图象.二、幂函数性质：1、所有的幂函数在0,都有定义，并且图像都通过点1,1；2、如果0a，则幂函数的图像经过原点，并且在区间0,上为增函数；如果0a，则幂函数的图像不经过原点，并且在区间0,上为增函数3、幂函数的图像及其奇偶性：令aqp（p、q互质）a00a1a1qpyx（p、q互质）p、q是奇数··2p是奇数、q是偶数p是偶数、q是奇数yx0yx特别提醒：（1）当a0时，图象过定点(0,0),(1,1)；在(0,+¥)上是增函数.（2）当a0时，图象过定点(1,1)；在(0,+¥)上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近.三、如图,,,,,abcdef的大小关系为：abcdef类型一幂函数的定义例1：在函数y＝1x2，y＝2x2，y＝x2＋x，y＝3x中，幂函数的个数为()A．0B．1C．2D．3练习1：有下列函数：①y＝3x2；②y＝x2＋1；③y＝－1x；④y＝1x；⑤y＝3；⑥y＝2x.其中，是幂函数的有________(只填序号)．OxyOxy··3练习2：函数y＝(k2－k－5)x2是幂函数，则实数k的值是()A．k＝3B．k＝－2C．k＝3或k＝－2D．k≠3且k≠－2类型二幂函数的图象和性质例2：幂函数y＝xm，y＝xn，y＝xp，y＝xq的图象如图，则将m、n、p、q的大小关系用“”连接起来结果是________．练习1：(2014～2015学年度江西鹰潭一中高一上学期月考)已知幂函数f(x)＝kxα的图象过点12，2，则k－α＝()A．12B．1C．32D．2练习2：(2014～2015学年度安徽宿州市十三校高一上学期期中测试)已知幂函数y＝(m2－5m－5)x2m＋1在(0，＋∞)上单调递减，则实数m＝()A．1B．－1C．6D．－1或6类型三函数值大小的比较例3：比较下列各组数的大小练习1：下列关系中正确的是()A．(12)23(15)23(12)13B．(12)23(12)13(15)23C．(15)23(12)13(12)23D．(15)23(12)23(12)13··4练习2：比较下列三个值的大小1.1，1.4，1.13；1、如图曲线是幂函数y＝xn在第一象限内的图象，已知n取±2，±12四个值，相应于曲线C1、C2、C3、C4的n依次为()A．－2，－12，12，2B．2，12，－12，－2C．－12，－2,2，12D．2，12，－2，－122、下列命题中正确的是()A．幂函数的图象不经过点(－1,1)B．幂函数的图象都经过点(0,0)和点(1,1)C．若幂函数f(x)＝xa是奇函数，则f(x)是定义域上的增函数D．幂函数的图象不可能出现在第四象限3、函数y＝|x|12的图象大致为()4、设函数y＝ax－2－12(a0，且a≠1)的图象恒过定点A，若点A在幂函数y＝xα的图象上，则该幂函数的单调递减区间是()A．(－∞，0)B．(0，＋∞)C．(－∞，0)，(0，＋∞)D．(－∞，＋∞)5、若函数f(x)＝(2m＋3)xm2－3是幂函数，则m的值为________．6、(2014～2015学年度浙江舟山中学高一上学期期中测试)已知幂函数y＝f(x)的图象过点(2,8)，则f(x)＝______________.··5__________________________________________________________________________________________________________________________________________________________________基础巩固1．如图所示为幂函数y＝xm与y＝xn在第一象限内的图象，则()A．－1＜n＜0＜m＜1B．n＜0＜m＜1C．－1＜n＜0，m＜1D．n＜－1，m＞12．函数y＝x3与函数y＝x13的图象()A．关于原点对称B．关于x轴对称C．关于y轴对称D．关于直线y＝x对称3．某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x)，则下列结论中正确的是()A．x22%B．x22%C．x＝22%D．x的大小由第一年产量确定4．某种细菌在培养过程中，每15min分裂一次(由1个分裂成2个)，则这种细菌由1个繁殖成212个需经过()A．12hB．4hC．3hD．2h5．某山区为加强环境保护，绿色植被的面积每年都比上一年增长10.4%，那么，经过x年，绿色植被面积可以增长为原来的y倍，则函数y＝f(x)的图象大致为()··6能力提升6．若幂函数y＝(m2－3m＋3)xm2－m－2的图象不过原点，则m是__________．7．如果幂函数y＝xa的图象，当0x1时，在直线y＝x的上方，那么a的取值范围是________．8.已知函数f(x)＝(m2＋2m)·xm2＋m－1，m为何值时，f(x)是(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数．9．定义函数f(x)＝max{x2，x－2}，x∈(－∞，0)∪(0，＋∞)，求f(x)的最小值．10.已知幂函数y＝xm2－2m－3(m∈Z)的图象与x、y轴都无公共点，且关于y轴对称，求出m的值。课程顾问签字：教学主管签字：