安徽省2023届高三上学期第一次模拟测试数学

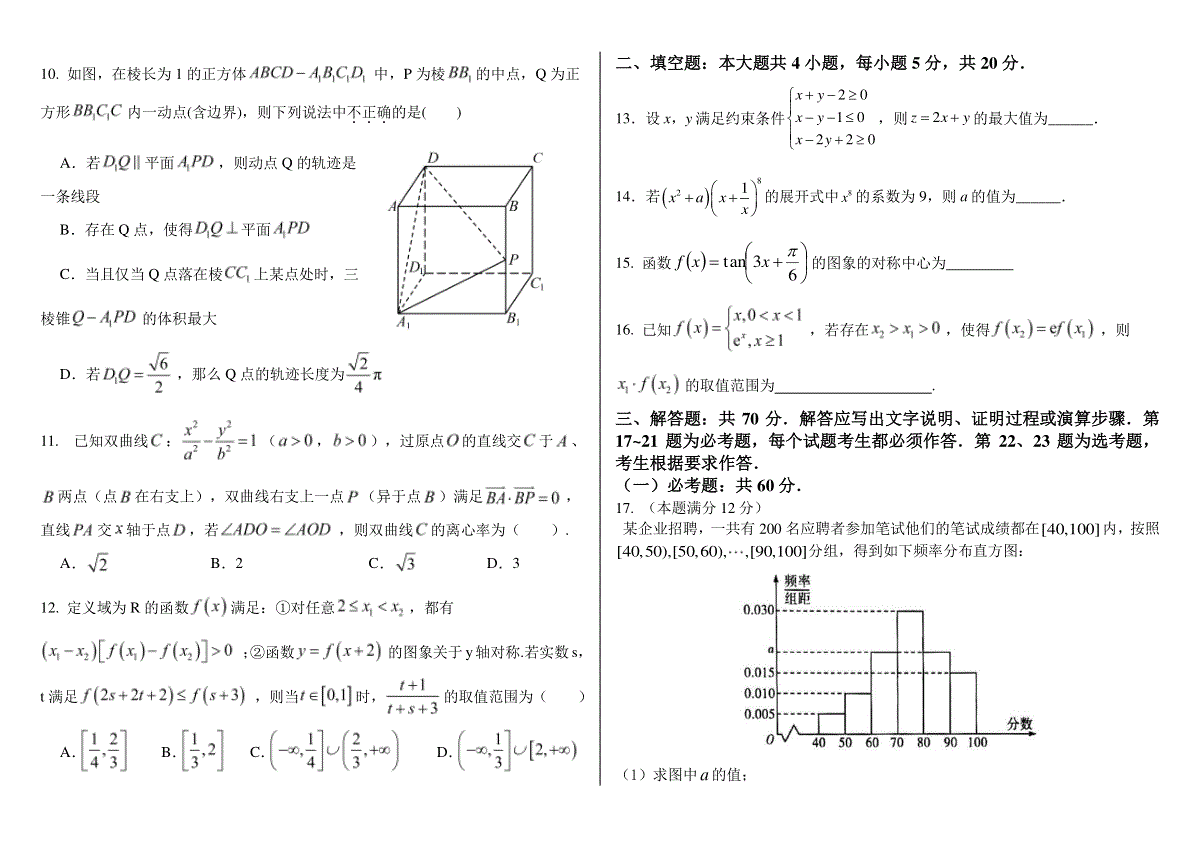
绝密★启用前安徽省2023届高三上学期第一次模拟测试数学试卷注意：1.考试总分150分，时间120分钟。2.考试结束后，请将试题卷与答题卷一并上交。一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集{1,2,3,4,5}U，集合{1,2,4}A，{2,3}B，则UUAB痧（）A．{2}B．{5}C．{1,3,4,5}D．{1,2,3,4}2．设31i2z，则z（）A．22B．2C．1D．23．已知向量(3,0)a，(1,1)b，且(2)abrr//(2)akb，则实数k的值是（）A．2B．2C．4D．44．已知等差数列1a，2a，3a，…，1na，na，前6项和为10，最后6项和为110，所有项和为360，则该数列的项数n（）A．26B．30C．36D．485．已知实数a，b满足2log1,01aaba，则21log4baa的最小值为（）A．0B．1C．1D．不存在6．如图，在三棱台111ABCABC中，1AA平面ABC，90ABC，111111AAABBC，2AB，则AC与平面11BCCB所成的角为（）A．30°B．45C．60D．907．为推动就业与培养有机联动、人才供需有效对接，促进高校毕业生更加充分更高质量就业，教育部今年首次实施供需对接就业育人项目．现安排甲、乙两所高校与3家用人单位开展项目对接，若每所高校至少对接两家用人单位，则两所高校的选择涉及到全部3家用人单位的概率为（）A．12B．23C．34D．13168．已知数列na的各项互异，且1110,2Nnnnanaa，则112231nnnaaaaaaaa（）A．14B．12C．2D．49.千百年来,我国劳动人民在生产实践中根据云的形状、走向速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩销云,地上雨淋林”“日落云里走,雨在半夜后”....小明同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如右2x2列联表:并计算得到K2=19.05,下列小明对地区天气判断正确的是A.夜晚下雨的概率约为51B.未出现“日落云里走”,但夜晚下雨的概率约为21C.出现“日落云里走”,有99.9%的把握认为夜晚会下雨D.有99.9%的把握认为“日落云里走是否出现”与“当晚是否下雨”有关。10.如图，在棱长为1的正方体中，P为棱的中点，Q为正方形内一动点(含边界)，则下列说法中不正确．．．的是()A．若平面，则动点Q的轨迹是一条线段B．存在Q点，使得平面C．当且仅当Q点落在棱上某点处时，三棱锥的体积最大D．若，那么Q点的轨迹长度为11.已知双曲线：（，），过原点的直线交于、两点（点在右支上），双曲线右支上一点（异于点）满足，直线交轴于点，若，则双曲线的离心率为（）.A．B．2C．D．312.定义域为R的函数满足：①对任意，都有；②函数的图象关于y轴对称.若实数s，t满足，则当时，的取值范围为（）A．B．C．D．二、填空题：本大题共4小题，每小题5分，共20分．13．设x，y满足约束条件2010220xyxyxy，则2zxy的最大值为______．14．若821xaxx的展开式中8x的系数为9，则a的值为______．15.函数63tanxxf的图象的对称中心为16.已知，若存在，使得，则的取值范围为.三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17.（本题满分12分）某企业招聘，一共有200名应聘者参加笔试他们的笔试成绩都在[40,100]内，按照[40,50),[50,60),,[90,100]分组，得到如下频率分布直方图：（1）求图中a的值；（2）求全体应聘者笔试成绩的平均数；（每组数据以区间中点值为代表）（3）该企业根据笔试成绩从高到低进行录取，若计划录取150人，估计应该把录取的分数线定为多少．18.（本题满分12分）在平面五边形ABCDE中，已知，，，，，（1）当时，求DC；（2）当五边形ABCDE的面积时，求BC的取值范围．19.（本题满分12分）如图，正方形ABCD与直角梯形ADEF所在平面相互垂直，90ADE，//AFDE，22ADDEAF.（1）求证：//AC平面BEF；（2）求点D到平面BEF的距离.20.（本题满分12分）已知函数()ln1lnfxxxxx．（1）设函数()yfx在1x和xe处的切线交直线1y于,MN两点，求||MN；（2）设0fx为函数()yfx的最小值，求证：0102fx．21.（本题满分12分）如图，椭圆的两顶点，，离心率，过y轴上的点的直线l与椭圆交于C，D两点，并与x轴交于点P，直线与直线交于点Q.（1）当且时，求直线l的方程；（2）当点P异于A，B两点时，设点P与点Q横坐标分别为，，是否存在常数使成立，若存在，求出的值；若不存在，请说明理由.（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．（共2题；共10分）[选修4—4：坐标系与参数方程]22.在平面直角坐标系xOy中，圆1C的圆心坐标为1,1且过原点，椭圆E的参数方程为2cossinxy（为参数）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线2C的极坐标方程为06.（1）求圆1C的极坐标方程和曲线2C的普通方程；（2）若曲线2C与圆1C相交于异于原点的点P，M是椭圆E上的动点，求OPM面积的最大值.[选修4—5：不等式选讲]23.已知函数()|1||1|fxxax．（Ⅰ）当2a时，解不等式5)(xf；（Ⅱ）当1a时，若存在实数x，使得21()mfx成立，求实数m的取值范围．此此此空空空白白白页页页，，，请请请勿勿勿答答答题题题！！！此此此空空空白白白页页页，，，请请请勿勿勿答答答题题题！！！