当前位置:首页 > 中学教育 > 初中教育 > 教案2(平行四边形)
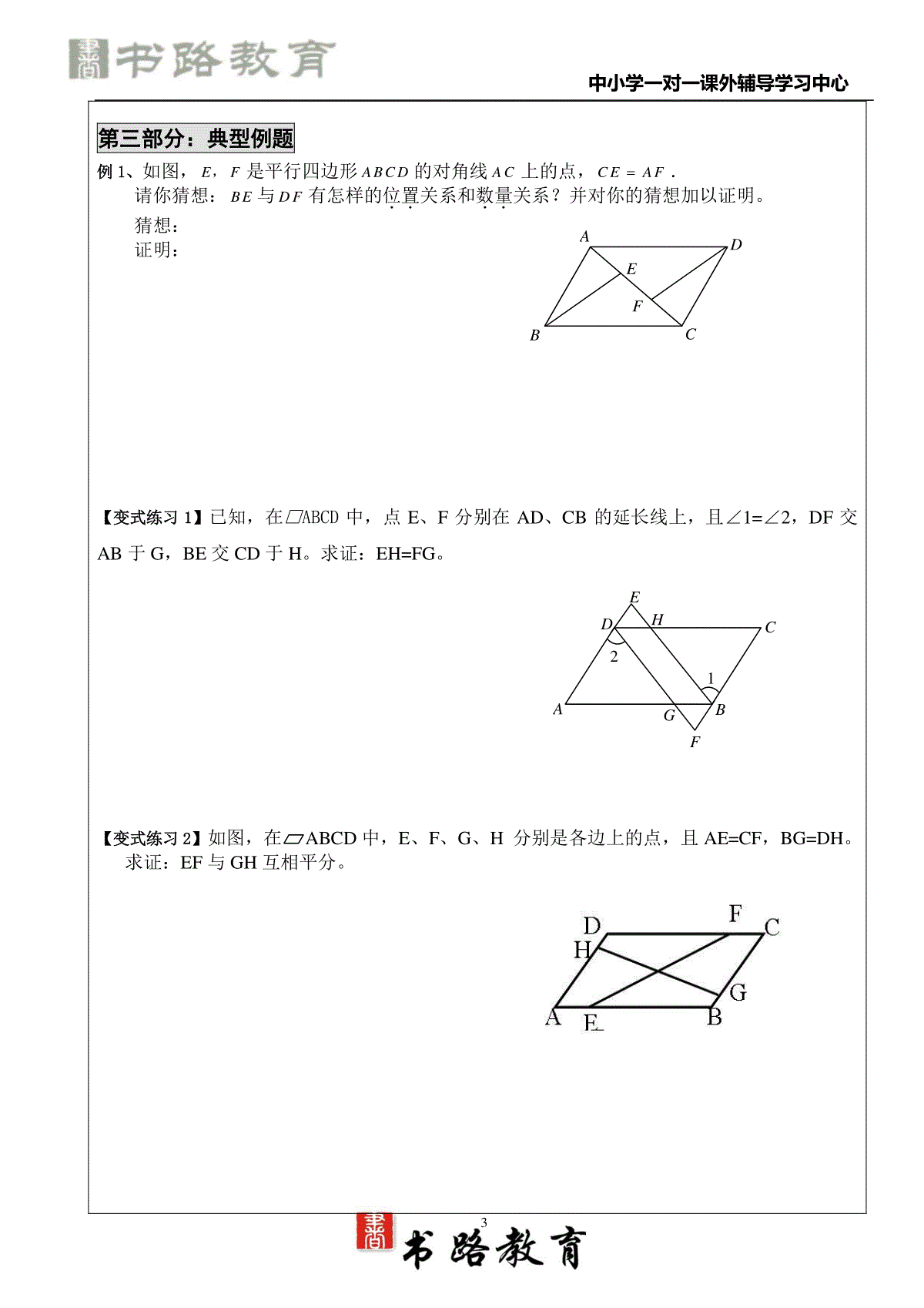
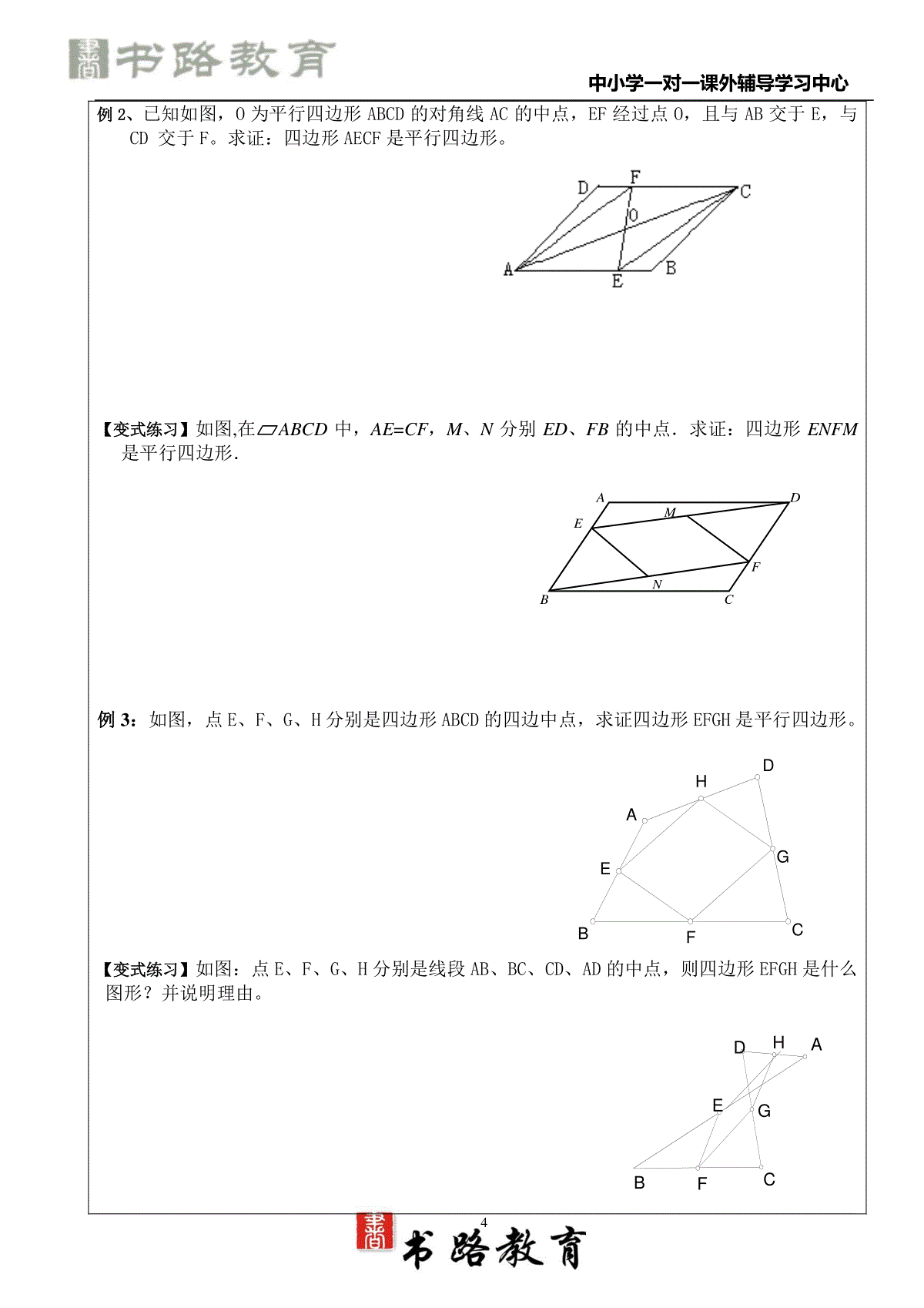
中小学一对一课外辅导学习中心1书路教育学科教师辅导讲义教学主题平行四边形教学目标理解并掌握平行四边形的概念和平行四边形的性质.重点平行四边形的性质与判定方法.难点综合运用平行四边形的性质和判定方法进行有关的论证和计算.第一部分:知识点回顾知识点1平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。记作“□ABCD”。知识点2平行四边形的性质:边:对边平行且相等。角:对角相等,邻角互补。对角线:对角线互相平分。1、(2010•苏州)如图,在平行四边形ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是.2、如图所示,平行四边形ABCD的周长是18cm,对角线AC、BD相交于点O,若△AOD与△AOB的周长差是5cm,则边AB的长是cm.知识点3平行四边形的判定:边:两组对边分别平行的四边形是平行四边形。两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形。角:两组对角分别相等的四边形是平行四边形。对角线:对角线互相平分的四边形是平行四边形。ABCD中小学一对一课外辅导学习中心21、(2011•郴州)如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是()A.AB=DC,AD=BCB.AB∥DC,AD∥BCC.AB∥DC,AD=BCD.AB∥DC,AB=DC2、(2011•泰州)四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有()A.1组B.2组C.3组D.4组知识点4两条平行线的距离。定义:在两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离。性质:两平行线间距离处处相等。已知如图直线m∥n,A、B为直线n上两点,C、D为直线m上两点,BC与AD交于点O,则图中面积相等的三角形有()A.1对B.2对C.3对D.4对知识点5三角形的中位线定义:连接三角形两边中点的线段是三角形的中位线。性质:三角形的中位线平行于第三边且等于第三边的一半。(2012•德阳)点D、E分别是△ABC的边AB、AC的中点,连接DE,若DE=5,则BC=第二部分:例题剖析已知:如图,E、F是平行四边形ABCD对角线AC上两点,且AE=CF。求证:四边形BFDE是平行四边形。ABCDEF中小学一对一课外辅导学习中心3第三部分:典型例题例1、如图,EF,是平行四边形ABCD的对角线AC上的点,CEAF.请你猜想:BE与DF有怎样的位置..关系和数量..关系?并对你的猜想加以证明。猜想:证明:【变式练习1】已知,在□ABCD中,点E、F分别在AD、CB的延长线上,且∠1=∠2,DF交AB于G,BE交CD于H。求证:EH=FG。【变式练习2】如图,在ABCD中,E、F、G、H分别是各边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。AGFBCDHE21ABCDEF中小学一对一课外辅导学习中心4例2、已知如图,O为平行四边形ABCD的对角线AC的中点,EF经过点O,且与AB交于E,与CD交于F。求证:四边形AECF是平行四边形。【变式练习】如图,在ABCD中,AE=CF,M、N分别ED、FB的中点.求证:四边形ENFM是平行四边形.例3:如图,点E、F、G、H分别是四边形ABCD的四边中点,求证四边形EFGH是平行四边形。【变式练习】如图:点E、F、G、H分别是线段AB、BC、CD、AD的中点,则四边形EFGH是什么图形?并说明理由。ABFCMDNEABCDEFGHABCDEFGH中小学一对一课外辅导学习中心5第四部分:思维误区误区一:不能正确地理解平行四边形的判定方法例:下列能判定四边形是平行四边形的条件是()A、一组对边平行,另一组对边相等B、一组对边平行,一组对角相等C、一组对边平行,一组邻角互补D、一组对边相等,一组邻角相等纠错秘方:一组对边平行且相等的四边形才是平行四边形,而一组对边平行,另一组对边相等的四边形有可能是平行四边形,也有可能是等腰梯形。误区二:不注意分类在□ABCD中,AE平分∠DAB,交BC于E,将BC分为5和4两部分,求平行四边形的周长。错解:如图,∵四边形ABCD是平行四边形∴AD∥BC从而有∠DAE=∠AEB由AE平分∠DAB∴∠BAE=∠DAE∴∠BAE=∠AEB∴AB=BE=5∴平行四边形的周长=AB+BC+CD+AD=5+9+5+9=28纠错秘方:本题是无图题,错解只看到两部分,但没有弄清楚哪一部分为5,哪一部分为4,忽略了分类讨论。正解:如图,∵四边形ABCD是平行四边形∴AD∥BC从而有∠DAE=∠AEB由AE平分∠DAB∴∠BAE=∠DAE∴∠BAE=∠AEB∴AB=BE当AB=BE=5时,平行四边形的周长=AB+BC+CD+AD=5+9+5+9=28当AB=BE=4时,平行四边形的周长=AB+BC+CD+AD=4+9+4+9=26误区三:错误地运用条件如图,已知□ABCD中,过对角线的交点O的直线交AD、CB的延长线于E和F,证明:DE=BF纠错秘方:本题误区主要在于以为EF与AC互相平分是已知条件,因为只有平行四边形的对角线是互相平分的,而EF不是对角线,所以不能直接用。ABCDE中小学一对一课外辅导学习中心6第五部分:方法规律概念规律关键平行四边形的定义两组对边分别平行平行四边形的性质合理运用到题中,选取正确快捷的方法平行四边形的判定结合图形与条件,选择正确的判定方法三角形的中位线注意构造和应用第六部分:巩固练习A组1、在ABCD中,:2:7AB,则C____°2、已知ABCD的周长为30cm,:2:3ABBC,则AB____cm。3、已知四边形ABCD中,AB∥DC,则可以添加条件____________________,使四边形ABCD是平行四边形。(图形中不再添加辅助线)4、□ABCD中,AC、BD相交于点O,8,12,20ABACBD,则AOB的周长为_______,AOB的面积为_______。5、在下列给出的条件中,不能判定四边形ABCD为平行四边形的是()A.AB平行且等于CDB.,ACBDC.,ABADBCCDD.1,2OAOCOBBD6、能判别一个四边形是平行四边形的条件是()A.一组对边相等,另一组对边平行B.一组对边平行,一组对角互补C.一组对角相等,一组邻角互补D.一组对角互补,另一组对角相等7、平行四边形不具有的性质是()。A.对边平行B.对边相等C.对角线互相垂直D.对角线互相平分8、□ABCD中,∠A:∠B:∠C:∠D的值可以是()。A.1:2:3:4B.1:2:2:1C.2:2:1:1D.2:1:2:19、如图,DE是△ABC的中位线,若BC的长为3cm,则DE的长是()A.2cmB.1.5cmC.1.2cmD.1cm中小学一对一课外辅导学习中心710、若□ABCD的∠BAD的平分线交BC于E,且AE=BE,则∠BCD等于()。A.30°B.60°C.90°D.120°11、如图,平行四边形ABCD中,AE平分∠DAB,∠B=100°,则∠DEA等于()A.100°B.80°C.60°D.40°12、顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形13、(2010•毕节地区)如图,已知:平行四边形ABCD中,∠BCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G.求证:AE=DG.14、已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC,求证:BE=CF。15、已知:如图,平行四边形ABCD中,点E、F分别在CD、AB上DF∥BE,EF交BD于点O.求证:EO=OF.中小学一对一课外辅导学习中心8ABFOCED16、如图,在四边形ABCD中,AD∥BC,OE=OF,OA=OC.求证:四边形ABCD是平行四边形.B组1、如图所示,在▱ABCD中,AB=5,AD=8,DE平分∠ADC,则BE=2、(2011•聊城)如图,在平行四边形ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=3cm,则AD的长是cm.3、从平行四边形的一个锐角的顶点做两条高线,如果这两条高线的夹角是135°,这个平行四边形的锐角的度数是.4、如图,P是四边形ABCD的DC边上的一个动点,当四边形ABCD满足条件时,△PBA的面积始终保持不变。(注:只需填上你认为正确的一种条件即可,不必考虑所有可能的情形)5、如图,ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,则△OBC的周长是_______cm.6、如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为()A.8.3B.9.6C.12.6D.13.6中小学一对一课外辅导学习中心97、如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E、F,连接ED,BF.求证:∠1=∠28、如图,点A、D、B、E在同一直线上,AD=BE,AC=DF,AC∥DF,请从图中找出一个与∠E相等的角,并加以证明。(不再添加其他的字母与线段)9、已知:ABCD中,直线MN//AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。求证:PM=QN。10、如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于E,如果∠CEM=40°,则∠DME的度数是多少度。11、如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不必证明)(温馨提示:在图(1)中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线的性质,可证明∠BME=∠CNE)(1)如图(2),在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交CD、BA于点M、N,判断△OMN的形状,请直接写出结论.(2)如图(3)中,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD形状并证明.ABCDMNPQ21FABDCE中小学一对一课外辅导学习中心10第七部分:中考体验1、(2011.广州)已知□ABCD的周长为32,AB=4,则BC=()A.4B.121C.24D.282、(2009·桂林)如图,在平行四边形ABCD中,AC、BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为()A、3B、6C、12D、243、(2009•茂名)杨伯家小院子的四棵小树E、F、G、H刚好在其梯形院子ABCD各边的中点上,若在四边形EFGH种上小草,则这块草地的形状是()A.平行四边形B.矩形C.正方形D.菱形4、(浙江金华)国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图2),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB//EF//DC,BC//GH//AD,那么下列说法中错误的是()A.红花、绿花种植面积一定相等B.紫花、橙花种植面积一定相等C.红花、蓝花种植面积一定相等D.蓝花、黄花种植面积一定相等5.(2009广州)如图6,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=24,则ΔCEF的周长为()(A)8(B)9.5(C)10(D)11.5)图(121HNMFEDCABNMEFOABCD)图(2ECBFADG)图(3中小学一对一课外辅导学习中心116、(福建龙岩)如图(3),在□ABCD中,E、F分别为AD、BC边上的一点,若再增加一个条件_____________,就可推得B



 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:教案2(平行四边形)
链接地址:https://www.777doc.com/doc-2421118 .html