中考二次函数综合题复习(含答案)

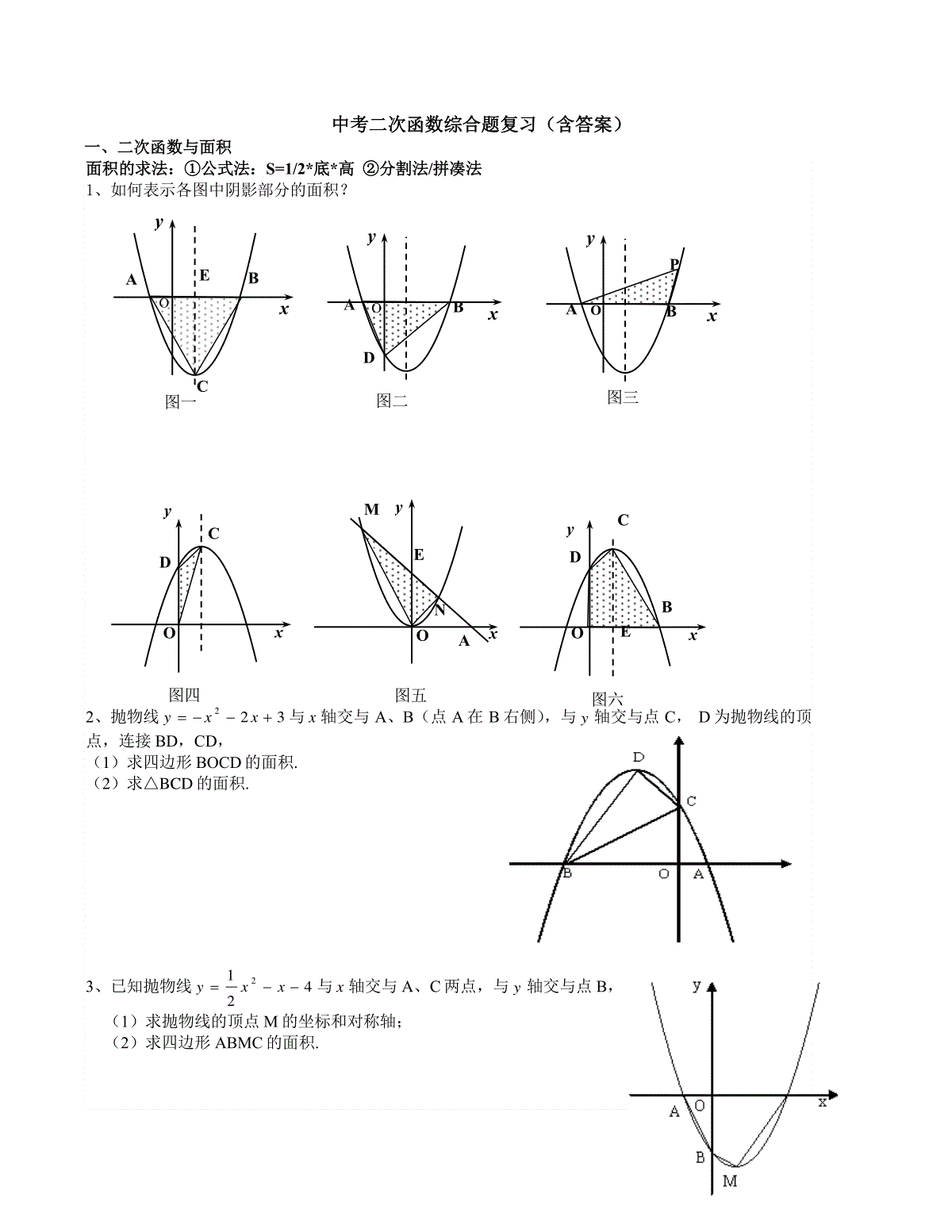
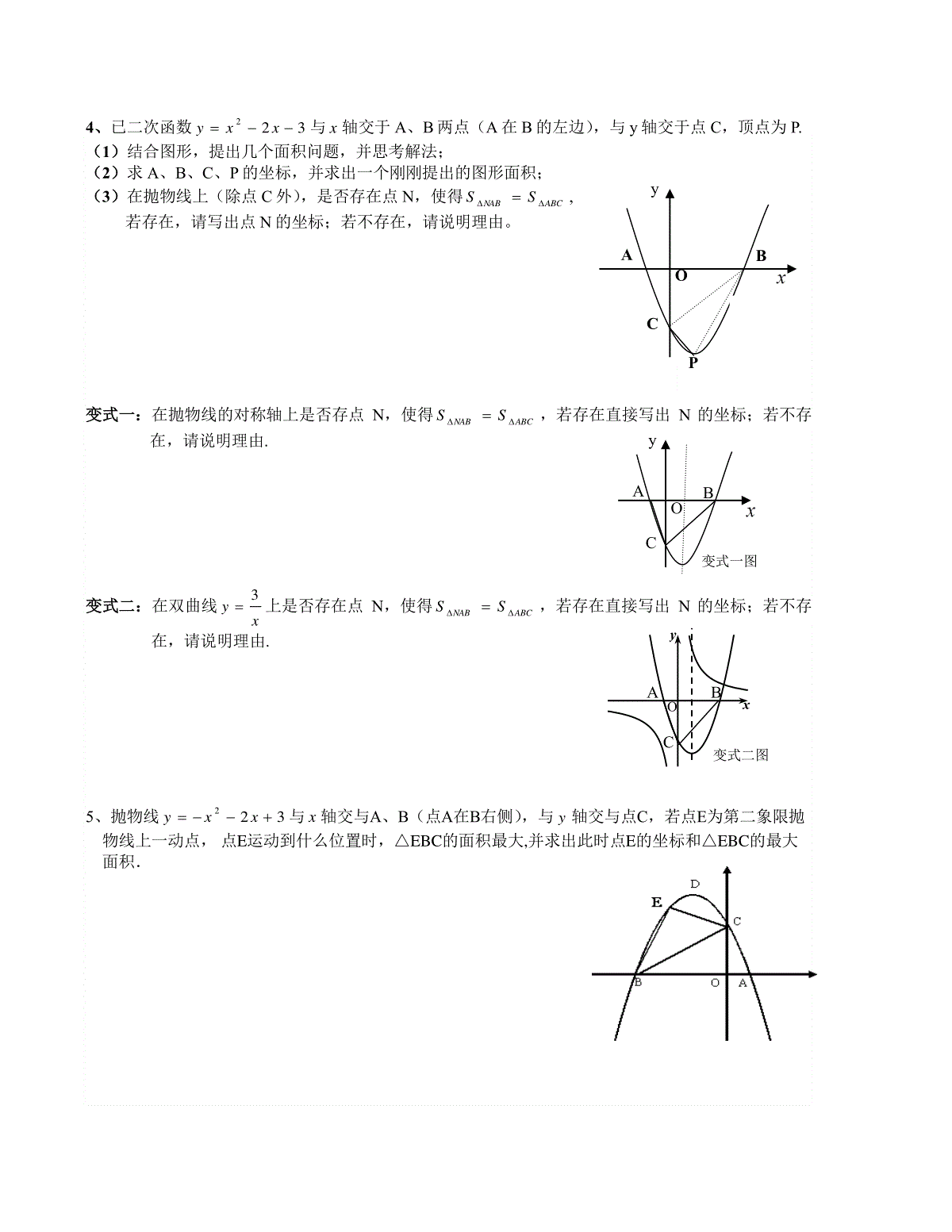
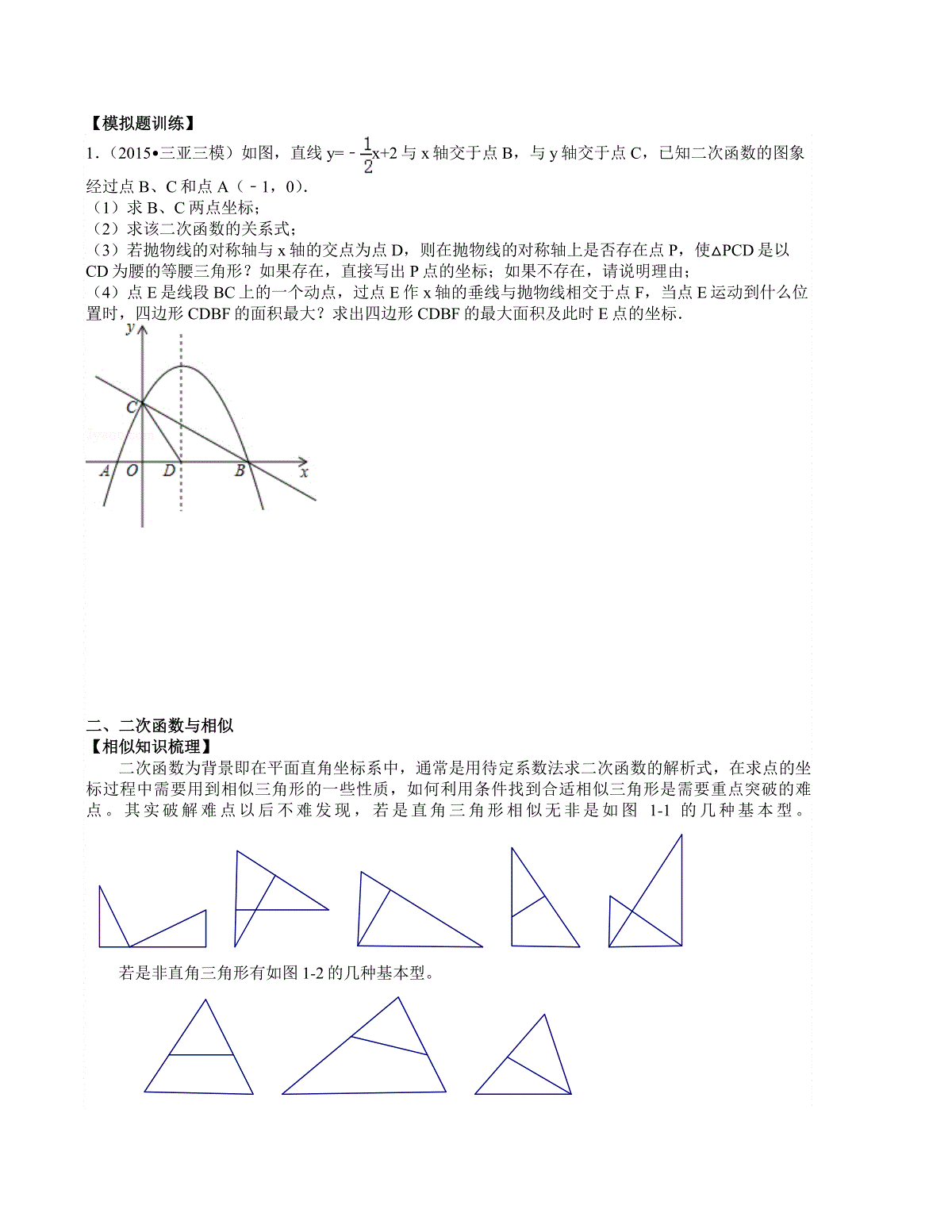
中考二次函数综合题复习（含答案）一、二次函数与面积面积的求法：①公式法：S=1/2*底*高②分割法/拼凑法1、如何表示各图中阴影部分的面积？2、抛物线322xxy与x轴交与A、B（点A在B右侧），与y轴交与点C，D为抛物线的顶点，连接BD，CD，（1）求四边形BOCD的面积.（2）求△BCD的面积.3、已知抛物线4212xxy与x轴交与A、C两点，与y轴交与点B，（1）求抛物线的顶点M的坐标和对称轴；（2）求四边形ABMC的面积.xyOMENA图五OxyDC图四xyODCEB图六PxyOAB图三xyOABD图二ExyOABC图一4、已二次函数322xxy与x轴交于A、B两点（A在B的左边），与y轴交于点C，顶点为P.（1）结合图形，提出几个面积问题，并思考解法；（2）求A、B、C、P的坐标，并求出一个刚刚提出的图形面积；（3）在抛物线上（除点C外），是否存在点N，使得ABCNABSS,若存在，请写出点N的坐标；若不存在，请说明理由。变式一：在抛物线的对称轴上是否存点N，使得ABCNABSS，若存在直接写出N的坐标；若不存在，请说明理由.变式二：在双曲线3yx上是否存在点N，使得ABCNABSS，若存在直接写出N的坐标；若不存在，请说明理由.5、抛物线322xxy与x轴交与A、B（点A在B右侧），与y轴交与点C，若点E为第二象限抛物线上一动点，点E运动到什么位置时，△EBC的面积最大,并求出此时点E的坐标和△EBC的最大面积．CPOAByAyBOC变式一图AxyOBC变式二图【模拟题训练】1．（2015•三亚三模）如图，直线y=﹣x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点A（﹣1，0）．（1）求B、C两点坐标；（2）求该二次函数的关系式；（3）若抛物线的对称轴与x轴的交点为点D，则在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；（4）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．二、二次函数与相似【相似知识梳理】二次函数为背景即在平面直角坐标系中，通常是用待定系数法求二次函数的解析式，在求点的坐标过程中需要用到相似三角形的一些性质，如何利用条件找到合适相似三角形是需要重点突破的难点。其实破解难点以后不难发现，若是直角三角形相似无非是如图1-1的几种基本型。若是非直角三角形有如图1-2的几种基本型。利用几何定理和性质或者代数方法建议方程求解都是常用的方法。【例题点拨】【例1】如图1-3，二次函数22bxaxy的图像与x轴相交于点A、B，与y轴相交于点C，经过点A的直线2kxy与y轴相交于点D，与直线BC垂直于点E，已知AB=3，求这个二次函数的解析式。【例2】如图1-4，直角坐标平面内，二次函数图象的顶点坐标为C3,4，且在x轴上截得的线段AB的长为6.（1）求二次函数解析式；（2）在x轴上方的抛物线上，是否存在点D，使得以A、B、D三点为顶点的三角形与△ABC相似？若存在，求出点D的坐标，若不存在，请说明理由。【例3】如图1-6，在平面直角坐标系中，二次函数cbxxy241-的图像经过点A（4,0），C（0,2）。（1）试求这个二次函数的解析式，并判断点B（-2,0）是否在该函数的图像上；（2）设所求函数图像的对称轴与x轴交于点D，点E在对称轴上，若以点C、D、E为顶点的三角形与△ABC相似，试求点E的坐标。YXED2D1HCBAO图1-3BEADOCxy图1-6CA1Oyx【模拟题训练】2．（2015•崇明县一模）如图，已知抛物线y=x2+bx+c经过直线y=﹣+1与坐标轴的两个交点A、B，点C为抛物线上的一点，且∠ABC=90°．（1）求抛物线的解析式；（2）求点C坐标；（3）直线y=﹣x+1上是否存在点P，使得△BCP与△OAB相似？若存在，请直接写出P点的坐标；若不存在，请说明理由．三、二次函数与垂直【方法总结】①应用勾股定理证明或利用垂直②三垂直模型【例1】：如图，直线l过等腰直角三角形ABC顶点B，A、C两点到直线l的距离分别是2和3，则AB的长是（）【例2】：在平面直角坐标系中，抛物线y=ax2+bx+c与x轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.（1）直接填写：a=，b=，顶点C的坐标为；（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；(第26题图)yxOCBA【例3】、如图，已知抛物线y=x2+bx-3a过点A（1,0），B(0,-3),与x轴交于另一点C.（1）求抛物线的解析式；（2）若在第三象限的抛物线上存在点P，使△PBC为以点B为直角顶点的直角三角形，求点P的坐标；（3）在（2）的条件下，在抛物线上是否存在一点Q，使以P,Q,B,C为顶点的四边形为直角梯形？若存在，请求出点Q的坐标；若不存在，请说明理由.【模拟题训练】3．（2015•普陀区一模）如图，在平面直角坐标系xOy中，点A（m，0）和点B（0，2m）（m＞0），点C在x轴上（不与点A重合）（1）当△BOC与△AOB相似时，请直接写出点C的坐标（用m表示）（2）当△BOC与△AOB全等时，二次函数y=﹣x2+bx+c的图象经过A、B、C三点，求m的值，并求点C的坐标（3）P是（2）的二次函数图象上的一点，∠APC=90°，求点P的坐标及∠ACP的度数．4．如图，已知抛物线y=x2﹣1的顶点坐标为M，与x轴交于A、B两点．（1）判断△MAB的形状，并说明理由；（2）过原点的任意直线（不与y轴重合）交抛物线于C、D两点，连接MC、MD，试判断MC、MD是否垂直，并说明理由．四、二次函数与线段题目类型：①求解线段长度（定值，最值）：充分利用勾股定理、全等、相似、特殊角（30°，45°，60°，90°，120°等）、特殊三角形（等腰△、等腰直角△、等边△）、特殊线（中位线、中垂线、角平分线、弦等）、对称、函数（一次函数、反比例函数、二次函数等）等知识。②判断线段长度关系：a=b,a=√2b,a+b=c,a+b=√2c,a2+b2=c2,a*b=c2【模拟题训练】5．（2015•山西模拟）如图1，P（m，n）是抛物线y=x2﹣1上任意一点，l是过点（0，﹣2）且与x轴平行的直线，过点P作直线PH⊥l，垂足为H．【特例探究】（1）填空，当m=0时，OP=_________，PH=_________；当m=4时，OP=_________，PH=_________．【猜想验证】（2）对任意m，n，猜想OP与PH大小关系，并证明你的猜想．【拓展应用】（3）如图2，如果图1中的抛物线y=x2﹣1变成y=x2﹣4x+3，直线l变成y=m（m＜﹣1）．已知抛物线y=x2﹣4x+3的顶点为M，交x轴于A、B两点，且B点坐标为（3，0），N是对称轴上的一点，直线y=m（m＜﹣1）与对称轴于点C，若对于抛物线上每一点都有：该点到直线y=m的距离等于该点到点N的距离．①用含m的代数式表示MC、MN及GN的长，并写出相应的解答过程；②求m的值及点N的坐标．五、二次函数与角度结题方法总结角度相等的利用和证明：①直接计算②平行线③等腰三角形④全等、相似三角形⑤角平分线性质⑥倒角（∠1=∠3，∠2=∠3→∠1=∠2）【构造三垂直模型法】例1：如图，在平面直角坐标系xOy中，点P为抛物线上一动点，点A的坐标为（4，2），若∠AOP=45°，则点P的坐标为()【直接计算】例2.如图，抛物线与x轴交于A，B两点，与y轴交于点C，点D是抛物线的对称轴与x轴的交点，点P是抛物线上一点，且∠DCP=30°，则符合题意的点P的坐标为()【与几何图形结合】例4、二次函数的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点，在二次函数的图象上是否存在点P，使得∠PAC为锐角？若存在，请你求出P点的横坐标取值范围；若不存在，请你说明理由。322xxy【利用相似】例3、已知抛物线的图象与轴交于、两点（点在点的左边），与轴交于点C（0，3），过点作轴的平行线与抛物线交于点，抛物线的顶点为，直线经过、两点.（1）求此抛物线的解析式；（2）连接、、，试比较和的大小，并说明你的理由.【模拟题训练】6．（2015•松江区一模）已知在平面直角坐标系xOy中，二次函数y=ax2+bx的图象经过点（1，﹣3）和点（﹣1，5）；（1）求这个二次函数的解析式；（2）将这个二次函数的图象向上平移，交y轴于点C，其纵坐标为m，请用m的代数式表示平移后函数图象顶点M的坐标；（3）在第（2）小题的条件下，如果点P的坐标为（2，3），CM平分∠PCO，求m的值．2yaxbxcxABAByCxDM5yxDMAMACBCMABACB六、二次函数与平行四边形解题方法总结：①平行线的性质（同位角，内错角，同旁内角）②比较一次函数k值③平行四边形的性质④注意多解性【模拟题训练】7．如图，抛物线y=x2+bx﹣3与x轴交于A、B两点（点A在点B左侧），直线l与抛物线交于A、C亮点，其中C的横坐标为2．（1）求A、C两点的坐标及直线AC的函数解析式；（2）P是线段AC上的一个动点，过点P作y轴的平行线交抛物线于点E，求△ACE面积的最大值；（3）点G是抛物线上的动点，在x轴上是否存在点F，使以A、C、F、G四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．七、二次函数与图形转换常见图像变换：①平移（上加下减，左加右减）②轴对称（折叠）【模拟题训练】8．（2014•西城区一模）抛物线y=x2﹣kx﹣3与x轴交于点A，B，与y轴交于点C，其中点B的坐标为（1+k，0）．（1）求抛物线对应的函数表达式；（2）将（1）中的抛物线沿对称轴向上平移，使其顶点M落在线段BC上，记该抛物线为G，求抛物线G所对应的函数表达式；（3）将线段BC平移得到线段B′C′（B的对应点为B′，C的对应点为C′），使其经过（2）中所得抛物线G的顶点M，且与抛物线G另有一个交点N，求点B′到直线OC′的距离h的取值范围．模拟训练题参考答案1考点：二次函数综合题．菁优网版权所有分析：（1）分别令解析式y=﹣x+2中x=0和y=0，求出点B、点C的坐标；（2）设二次函数的解析式为y=ax2+bx+c，将点A、B、C的坐标代入解析式，求出a、b、c的值，进而求得解析式；（3）由（2）的解析式求出顶点坐标，再由勾股定理求出CD的值，再以点C为圆心，CD为半径作弧交对称轴于P1，以点D为圆心CD为半径作圆交对称轴于点P2，P3，作CE垂直于对称轴与点E，由等腰三角形的性质及勾股定理就可以求出结论；（4）设出E点的坐标为（a，﹣a+2），就可以表示出F的坐标，由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式，由二次函数的性质就可以求出结论．解答：解：（1）令x=0，可得y=2，令y=0，可得x=4，即点B（4，0），C（0，2）；（2）设二次函数的解析式为y=ax2+bx+c，将点A、B、C的坐标代入解析式得，，解得：，即该二次函数的关系式为y=﹣x2+x+2；（3）∵y=﹣x2+x+2，∴y=﹣（x﹣）2+，∴抛物线的对称轴是x=．∴OD=．∵C（0，2），∴OC=2．在Rt△OCD中，由勾股定理，得CD=．∵△CDP是以CD为腰的等腰三角形，∴CP1=DP2=DP3=CD．如图1所示，作CH⊥x对称轴于H，∴HP1=HD=2，∴DP1=4．∴P1（，4），P2（，），P3（，﹣）；（4）当y=0时，0=﹣x2+x+2∴x1=﹣1，x2=4，∴B（4，0）．∵直线BC的解析式为：y=﹣x+2．如图2，过点C作CM⊥EF于M，设E（a，﹣a+2），F（a，﹣a2+a+2），∴EF=﹣a2+a