2.6应用一元二次方程(第二课时)

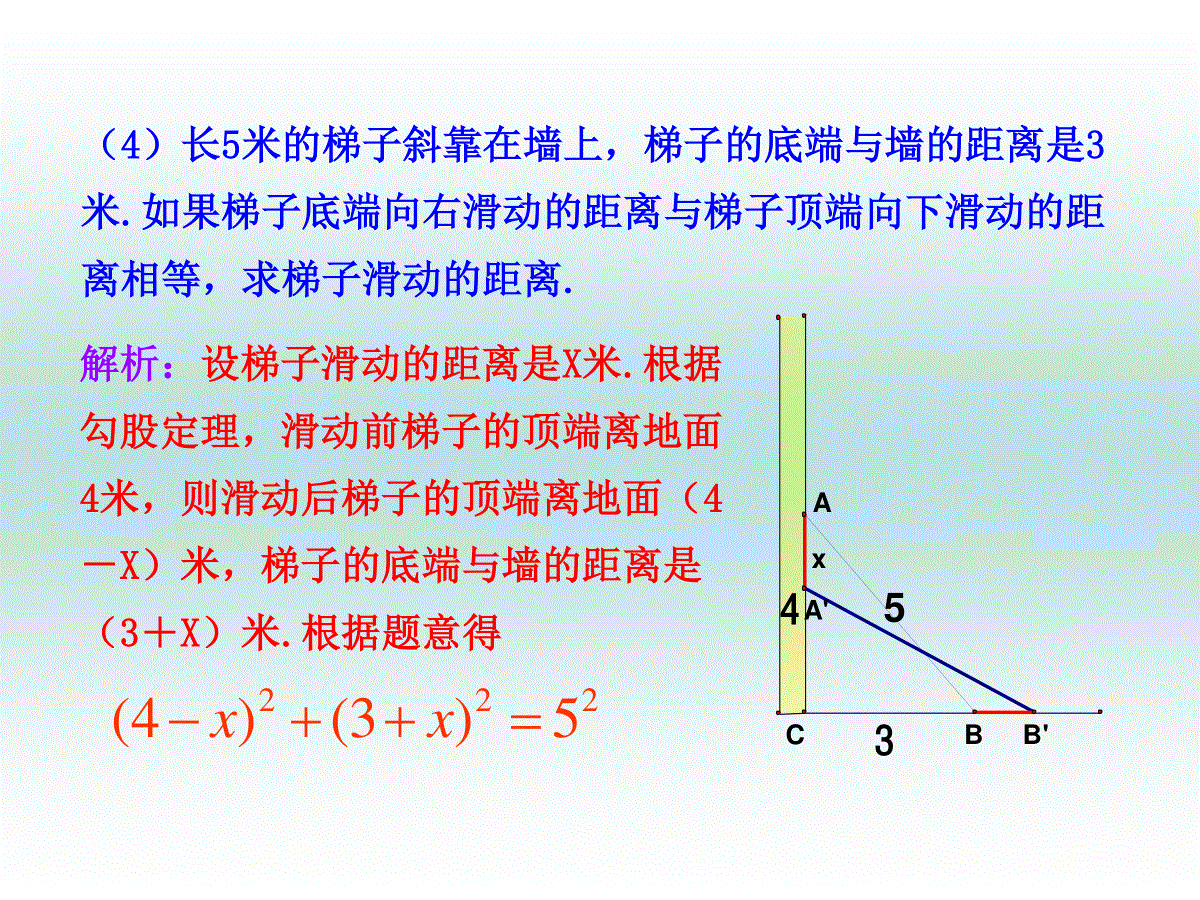
2.6应用一元二次方程1.你还记得什么叫方程？什么叫方程的解吗？2.什么是一元一次方程？它的一般形式是怎样的？3.我们知道了利用一元一次方程可以解决生活中的一些实际问题，你还记得利用一元一次方程解决实际问题的步骤吗?新课导入解析：设较短的长为X（cm）解析：该足球场一边的长是x米.（2）直角三角形三边的长都是整数，它的斜边长为11cm，两条直角边的差为7cm，求两直角边的长.22211)7(xx根据题意，得7140)2346(xx知识讲解（1）某足球场面积为7140m2,周长为346m，求该足球场的长和宽..x率是设平均每年增长的百分2.7)1(52x（3）我校图书馆的藏书在两年内从5万册增加到7.2万册，平均每年增长的百分率是多少？解析：根据题意，得2225)3()4(xx解析：设梯子滑动的距离是X米.根据勾股定理，滑动前梯子的顶端离地面4米，则滑动后梯子的顶端离地面（4－X）米，梯子的底端与墙的距离是（3＋X）米.根据题意得（4）长5米的梯子斜靠在墙上，梯子的底端与墙的距离是3米.如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等，求梯子滑动的距离.5x43BAB'CA'2.7)1(52x2225)3()4(xx特点:①都是整式方程;②只含一个未知数;③未知数的最高次数是2.像这样的等号两边都是整式,它们都只含有一个未知数，并且整理后未知数的最高次数是2，像这样的方程叫做一元二次方程.22211)7(xx7140)2346(xx071401732xx03672xx02.21052xx02xx023).4(1).3(1).2(1).1(222yxxxxxxx跟踪训练)0,0().7(0).6()2)(1(3).5(222为常数mmxcbxaxxxx下列方程中那些是一元二次方程√√√24)219(xx22x2.7)1(52x2225)3()4(xx0241922xx022x02.21052xx02xx把下列一元二次方程化简为右边为0的形式ax2+bx+c=0(a、b、c为常数且a≠0)一般地,任何一个关于x的一元二次方程都可以化为的形式,我们把(a,b,c为常数，a≠0）称为一元二次方程的一般形式.20axbxc20axbxc二次项系数一次项系数【例1】将下列方程化为一般形式，并分别指出它们的二次项、一次项和常数项及它们的系数：)2(5)1(3xxx105332xxx105332xxx02x(2)解析：010832xx10常数项为－88，其系数为－一次项：－x.3.32其系数为二次项：x12、系数为二次项：x0:0、系数一次项：0常数项：例题把下列方程化为一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项：方程一般形式二次项系数一次项系数常数项3x2=5x-1(x+2)(x-1)=64-7x2=03x2－5x＋1＝0x2+x－8＝03-5111-8-704或7x2-4＝070-4-7x2+4＝0跟踪训练x8m17m6m【例2】如图，一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，那么梯子的底端距墙____m数学化例题解析：由勾股定理可知，滑动前梯子底端距墙m；如果设梯子底端滑动xm，那么滑动后梯子底端距墙m；根据题意，可得方程：72＋(x＋6)2＝1026x＋6在上面的这个问题中，梯子底端滑动的距离x(m)满足方程(x+6)2+72=102，把这个方程化为一般形式为x2+12x-15=0．（1）小明认为底端也滑动了1m，他的说法正确吗?为什么?（2）底端滑动的距离可能是2m吗?可能是3m吗?为什么?不正确，因为x=1不满足方程．不正确，因为x=2，3不满足方程．（3）你能猜出滑动距离x(m)的大致范围吗?（4）x的整数部分是几?十分位是几?请同学们，自己算一算，注意组内同学交流哦！x00.511.52x2+12x-15-15-8.75-25.2513下面是小亮的求解过程：由此，他猜测1＜x＜1.5．进一步计算：x1.11.21.31.4x2+12x-15-0.590.842.293.76所以1.1＜x＜1.2，由此他猜测x整数部分是1，十分位部分是1．你的结果怎样的呢？用“两边夹”思想解一元二次方程的步骤：①在未知数x的取值范围内排除一部分取值；②根据题意所列的具体情况再次进行排除；③列出能反映未知数和方程的值的表格进行再次筛选；④最终得出未知数的最小取值范围或具体数据．【规律方法】上述求解是利用了“两边夹”的思想1．若是关于x的一元二次方程，则（）0322ppxpxAB0C0D01pppp、为任意实数、、、或2．7222mxxmm）若方程（是关于的一元二次方程，则m的值为________C随堂练习2m3．一元二次方程(1+3x)(x-3)=2x2+1化为一般形式为：，二次项系数为：，一次项系数为：，常数项为：.4．关于x的方程(m-1)x2+(m+1)x+3m+2=0,当m______时为一元一次方程；当m时为一元二次方程0482xx1-8-4=1≠15.一名跳水运动员进行10米跳台跳水训练，在正常情况下，运动员必须在距水面5米以前完成规定的翻腾动作，并且调整好入水姿势，否则就容易出现失误。假设运动员起跳后的运动时间t(秒)和运动员距水面的高度h(米)满足关系：h=10+2.5t-5t2，那么他最多有多长时间完成规定动作?解析：根据题意，得10+2.5t-5t2=5,即2t2-t-2=0列表：t01232t2-t-2-2-1413所以1＜t＜2,进一步列表计算：t1.11.21.31.42t2-t-2-0.68-0.32-0.080.52所以1.2＜t＜1.3,因此他完成动作的时间最多不超过1.3秒．本课小结1、一元二次方程的概念和一般形式；2、正确理解和掌握一般形式中的a≠0，“项”和“系数”.3、运用一元二次方程解决生活中的问题.通过本课时的学习，需要我们掌握：