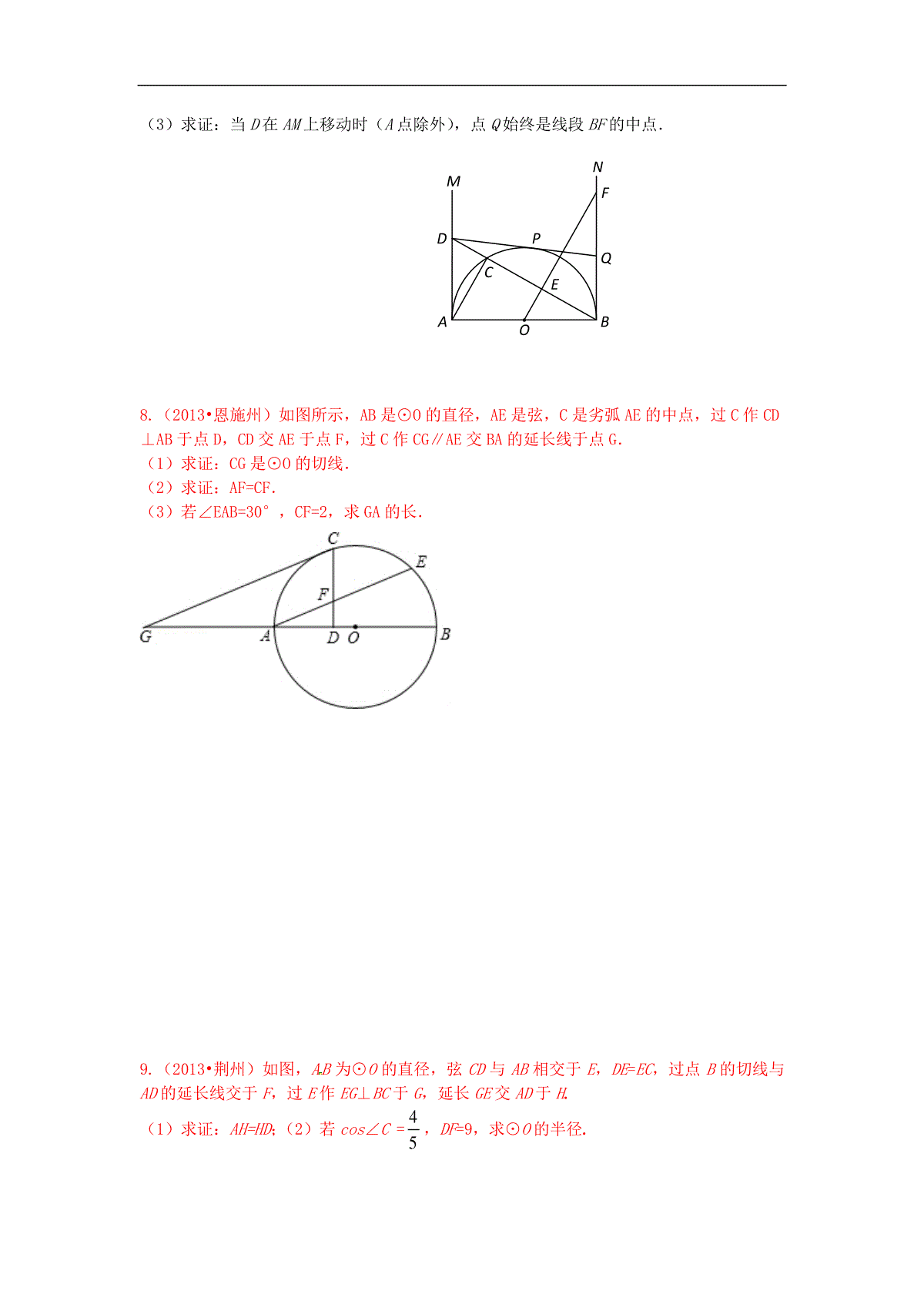
中考复习专题(六)——圆综合专训题型一:圆与直线1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)如果∠A=60º,则DE与DF有何数量关系?请说明理由;(3)如果AB=5,BC=6,求tan∠BAC的值.2.如图,在Rt△ABC中,∠C=90º,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E。(1)求证,ED为⊙O的切线;(2)如果⊙O的半径为23,ED=2,延长EO交⊙O于F,连接DF、AF求△ADF的面积。(第22题)FCBEDAOOADEBC3.(2012,兰州)如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是ABCEODFBC的中点,连接DE、OE.(1)判断DE与⊙O的位置关系并说明理由;(2)若tanC=52,DE=2,求AD的长.4.(2010兰州)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.(1)求证:PC是⊙O的切线;(2)求证:12BCAB;(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.5.如图,梯形ABCD是等腰梯形,且AD∥BC,O是腰CD的中点,以CD长为直径作圆,交BC于E,过E作EH⊥AB于H.EH=错误!未找到引用源。CD,(1)求证:OE∥AB;(2)求证:AB是⊙O的切线;(3)若BE=4BH,求错误!未找到引用源。的值.6.已知△ABC内接于⊙O,BT与⊙O相切于点B,点P在直线AB上,过点P作BC的平行线交直线BT于点E,交直线AC于点F.(1)如图,当点P在线段AB上时,求证:PA·PB=PE·PF;(2)当点P在BA延长线上时,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)若AB=42,cos∠EBA=13,求⊙O的半径.7.如图,AB是半圆O的直径,AB=2,射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.(1)求证:△ABC∽△OFB;(2)当△ABD与△BFO的面枳相等时,求BQ的长;CABEPOFT(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.8.(2013•恩施州)如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.(1)求证:CG是⊙O的切线.(2)求证:AF=CF.(3)若∠EAB=30°,CF=2,求GA的长.9.(2013•荆州)如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AD的延长线交于F,过E作EG⊥BC于G,延长GE交AD于H.(1)求证:AH=HD;(2)若cos∠C=45,DF=9,求⊙O的半径.OABCPQFNMDEHGFEDOCBA10.(2013•襄阳)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;(2)若AC=6,BC=8,求线段PD的长.11.(2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.(1)求证:DE是⊙O的切线;(2)求tan∠ABE的值;(3)若OA=2,求线段AP的长.12.(2013•钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.(1)求⊙O的半径OD;(2)求证:AE是⊙O的切线;(3)求图中两部分阴影面积的和.13.(2013•茂名)如图,在O中,弦AB与弦CD相交于点G,OACD于点E,过点B的直线与CD的延长线交于点F,ACBF∥.(1)若FGBFBG,求证:BF是O的切线;O(第24题图)GFEDCBA(2)若3tan4F,CDa,请用a表示O的半径;(3)求证:22GFGBDFGF.14.(2013•内江)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.(1)求证:BC平分∠PDB;(2)求证:BC2=AB•BD;(3)若PA=6,PC=6,求BD的长.题型二:圆与三角形1.如图,在锐角△ABC中,AC是最短边,以AC中点O为圆心,12AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.(1)求证:D是AE︵的中点;(2)求证:∠DAO=∠B+∠BAD;(3)若S△CEFS△OCD=12,且AC=4,求CF的长.2.(2011菏泽)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,(1)求证:△ABE∽△ADB;(2)求AB的长;(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.OABDCEF3.(2009本溪)如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.(1)判断直线BD和⊙O的位置关系,并给出证明;(2)当AB=10,BC=8时,求BD的长.4.如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD;(3)若EF=4,DE=3,求AD的长.5.(2010荆门)如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点.(1)求证:AC•CD=PC•BC;(2)当点P运动到AB弧中点时,求CD的长;(3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S.6.如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.(1)求证:DF垂直平分AC;(2)求证:FC=CE;(3)若弦AD=5㎝,AC=8㎝,求⊙O的半径.OHGFEDCBAPFOECBADG7.在ABCRt中,090C,AD是BAC的平分线,点E在AB边上,以AE为直径的⊙O经过点D.(1)判断BC与⊙O的位置关系,并说明理由;(2)求证:BDADDEAB;(3)设⊙O交AC于点F,连接EF,若tan∠BAC=34,求BCEF的值.8.如图,在ABCRt中,90C,AD是角平分线,ADDE交AB于E,ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.(1)求证:BC是⊙O的切线;(2)若2,34tanBEG,求⊙O的半径;(3)在(2)的条件下,求AP的长.CBDEOFA9.(四川省广安市)如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F.P是ED延长线上一点,且PC=PF.(1)求证:PC是⊙O的切线;(2)点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么?(3)在(2)的条件下,若OH=1,AH=2,求弦AC的长.10.如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.(1)求证:BC是⊙O的切线;(2)连接AF,BF,求∠ABF的度数;(3)如果CD=15,BE=10,sinA=513,求⊙O的半径.OABPDFHEC11.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,且∠CBD=∠BAC,OD交⊙O于点E.(1)求证:BD是⊙O的切线;(2)若点E为线段OD的中点,证明:以O、A、C、E为顶点的四边形是菱形;(3)作CF⊥AB于点F,连接AD交CF于点G(如图2),求FGFC的值.12.(2012湘潭)如图,在⊙O上位于直径AB的异侧有定点C和动点P,2AC=AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点.(1)如图1,求证:△PCD∽△ABC;(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.13.(2013•广东)如题24图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.14.(13•呼和浩特)如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.(1)求证:点F是AD的中点;(2)求cos∠AED的值;(3)如果BD=10,求半径CD的长.15.(2013•玉林)如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,(1)求∠DQN的度数;(2)求证:△DNQ≌△ANM;(3)猜想△DNQ的周长与AC的长度有什么关系。16.(2013•包头)如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.17.(2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=,求BN的长.题型三:圆与四边形1.(2012天水)如图,四边形ABCD内接于⊙O,已知直径AD=6,∠ABC=120°,∠ACB=45°,连接OB交AC于点E.(1)求AC的长.(2)求CE:EA的值.(3)在CB的延长线上取一点P,使CB=21BP,求证:直线PA与⊙O相切.2.(2012资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP(1)BD=DC吗?说明理由;(2)求∠BOP的度数;(3)求证:CP是⊙O的切线;AECDFBO3.(2012宜宾)如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2=.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C.D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A.B,连接AP、BP、AC.DB,且AC与DB的延长线交于点E.(1)求证:;(2)若PQ=2,试求∠E度数.4.(2011盐城)如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.(1)若AC=6,AB=10,求⊙O的半径;(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.5.(2012珠海)已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好




 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 wxg5577
wxg5577
共150篇文档
格式: doc
大小: 1.0 MB
时间: 2020-03-30
本文标题:中考复习专题圆综合
链接地址:https://www.777doc.com/doc-4636915 .html