当前位置:首页 > 临时分类 > 高三文科数学一轮复习不等式6-1
命题要点:不等式的性质′11年1考,′10年3考.A级(时间:40分钟满分:60分)一、选择题(每小题5分,共25分)1.“a+c>b+d”是“a>b且c>d”的().A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件解析“a+c>b+d”/⇒“a>b且c>d”,∴“充分性不成立”,“a>b且c>d”⇒“a+c>b+d”.∴必要性成立.答案A2.已知a<0,-1<b<0,那么下列不等式成立的是().A.a>ab>ab2B.ab2>ab>aC.ab>a>ab2D.ab>ab2>a解析由-1<b<0,可得b<b2<1,又a<0,∴ab>ab2>a.答案D3.(2011·浙江)若a,b为实数,则“0<ab<1”是“b<1a”的().A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件解析若0<ab<1,当a<0时,b>1a,当a>0时,b<1a,反之,若b<1a,当a<0时,ab>1.当a>0时,ab<1.答案D4.已知a,b,c满足c<b<a,且ac<0.那么下列选项中一定成立的是().A.ab>acB.c(b-a)<0C.cb2<ab2D.ac(a-c)>0解析由a>b>c且ac<0,得a>0,c<0,b∈R.所以可得ab>ac.答案A5.(2011·泉州质检)已知a1,a2∈(0,1),记M=a1a2,N=a1+a2-1,则M与N的大小关系是().A.M<NB.M>NC.M=ND.不确定解析M-N=a1a2-a1-a2+1=(a1-1)(a2-1)>0,故M>N.答案B二、填空题(每小题4分,共12分)6.已知M=2(a2+b2),N=2a-4b+2ab-7且a,b∈R,则M,N的大小关系为________.解析M-N=2(a2+b2)-(2a-4b+2ab-7)=(a2-2a+1)+(b2+4b+4)+(a2-2ab+b2)+2=(a-1)2+(b+2)2+(a-b)2+2>0,∴M>N.答案M>N7.下列四个不等式:①a<0<b;②b<a<0;③b<0<a;④0<b<a,其中能使1a<1b成立的充分条件有________(填序号).解析1a<1b⇔b-aab<0⇔b-a与ab异号,因此①②④能使b-a与ab异号.答案①②④8.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的取值范围是________(用区间表示).解析∵z=-12(x+y)+52(x-y),∴3≤-12(x+y)+52(x-y)≤8,∴z∈[3,8].答案[3,8]三、解答题(共23分)9.(11分)已知a>0,b>0,试比较M=a+b,N=a+b的大小.解M2-N2=(a+b)2-(a+b)2=a+b+2ab-a-b=2ab>0,∴M>N.10.(12分)已知f(x)=ax2-c且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.解由题意,得a-c=f1,4a-c=f2,解得a=13[f2-f1],c=-43f1+13f2.所以f(3)=9a-c=-53f(1)+83f(2).因为-4≤f(1)≤-1,所以53≤-53f(1)≤203,因为-1≤f(2)≤5,所以-83≤83f(2)≤403.两式相加,得-1≤f(3)≤20,故f(3)的取值范围是[-1,20].B级(时间:30分钟满分:40分)一、选择题(每小题5分,共10分)1.已知ab≠0,那么ab>1是ba<1的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件解析ab>1即a-bb>0,所以a>b>0,或a<b<0,此时ba<1成立;反之ba<1,所以a-ba>0,即a>b,a>0或a<0,a<b,此时不能得出ab>1.答案A2.(2011·淄博模拟)若a>0,b>0,则不等式-b<1x<a等价于().A.-1b<x<0或0<x<1aB.-1a<x<1bC.x<-1a或x>1bD.x<-1b或x>1a解析由题意知a>0,b>0,x≠0,(1)当x>0时,-b<1x<a⇔x>1a;(2)当x<0时,-b<1x<a⇔x<-1b.综上所述,不等式-b<1x<a⇔x<-1b或x>1a.答案D二、填空题(每小题4分,共8分)3.若角α,β满足-π2<α<β<π2,则2α-β的取值范围是________.解析∵-π2<α<β<π2,∴-π<2α<π,-π2<-β<π2,∴-3π2<2α-β<3π2,又∵2α-β=α+(α-β)<α<π2,∴-3π2<2α-β<π2.答案-3π2,π24.给出下列条件:①1<a<b;②0<a<b<1;③0<a<1<b.其中,能推出logb1b<loga1b<logab成立的条件的序号是________(填所有可能的条件的序号).解析∵logb1b=-1.若1<a<b,则1b<1a<1<b,∴loga1b<loga1a=-1,故条件①不可以;若0<a<b<1,b<1<1b<1a,∴logab>loga1b>loga1a=-1=logb1b,故条件②可以;若0<a<1<b,则0<1b<1,∴loga1b>0,logab<0,条件③不可以.答案②三、解答题(共22分)5.(10分)若a>b>0,c<d<0,e<0.求证:ea-c2>eb-d2.证明∵c<d<0,∴-c>-d>0.又∵a>b>0,∴a-c>b-d>0.∴(a-c)2>(b-d)2>0.∴0<1a-c2<1b-d2.又∵e<0,∴ea-c2>eb-d2.6.(12分)已知a∈R,试比较11-a与1+a的大小.解11-a-(1+a)=a21-a.①当a=0时,a21-a=0,∴11-a=1+a.②当a<1且a≠0时,a21-a>0,∴11-a>1+a.③当a>1时,a21-a<0,∴11-a<1+a.综上所述,当a=0时,11-a=1+a;当a<1且a≠0时,11-a>1+a;当a>1时,11-a<1+a.




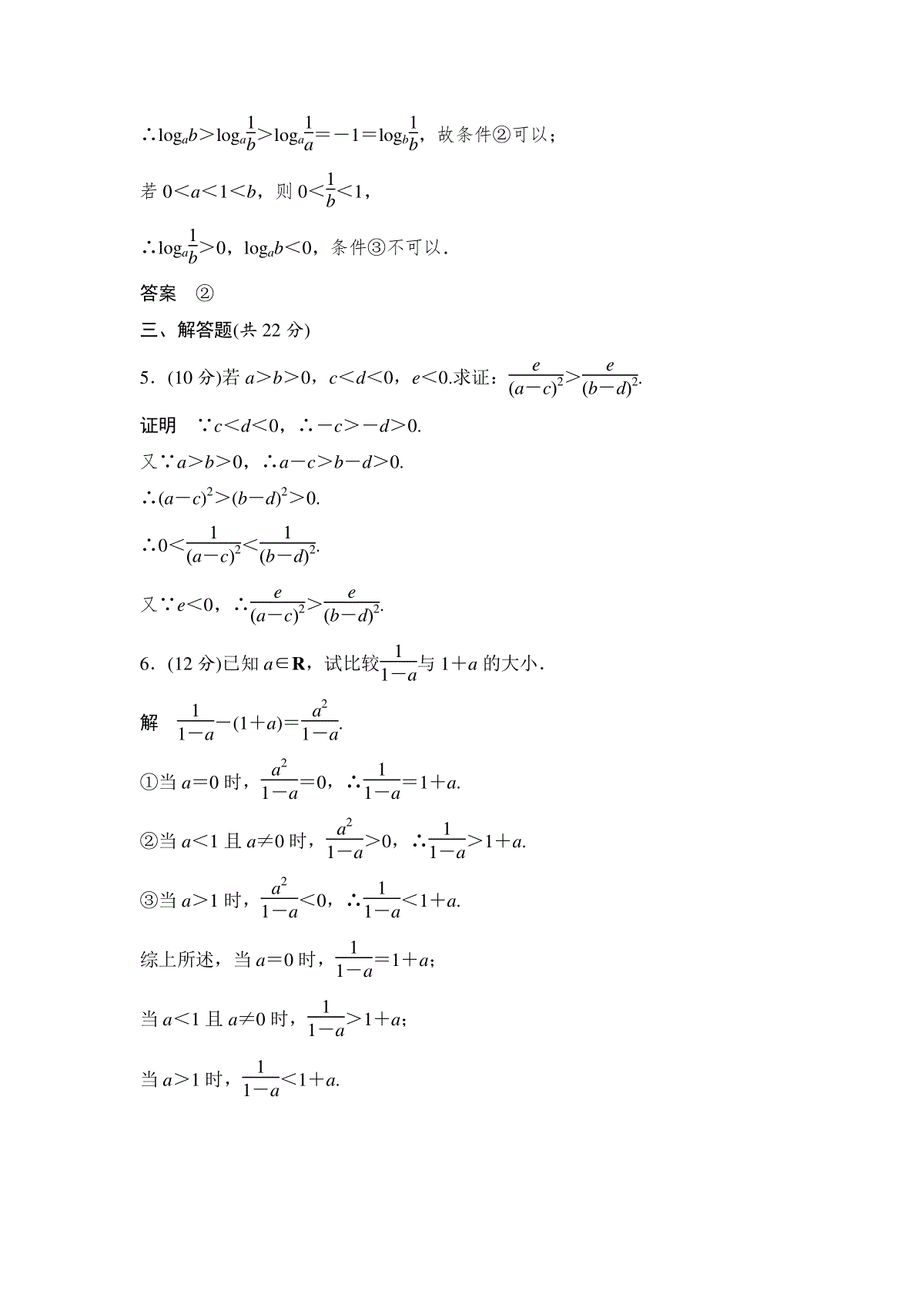
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:高三文科数学一轮复习不等式6-1
链接地址:https://www.777doc.com/doc-1936400 .html