相平衡6-2

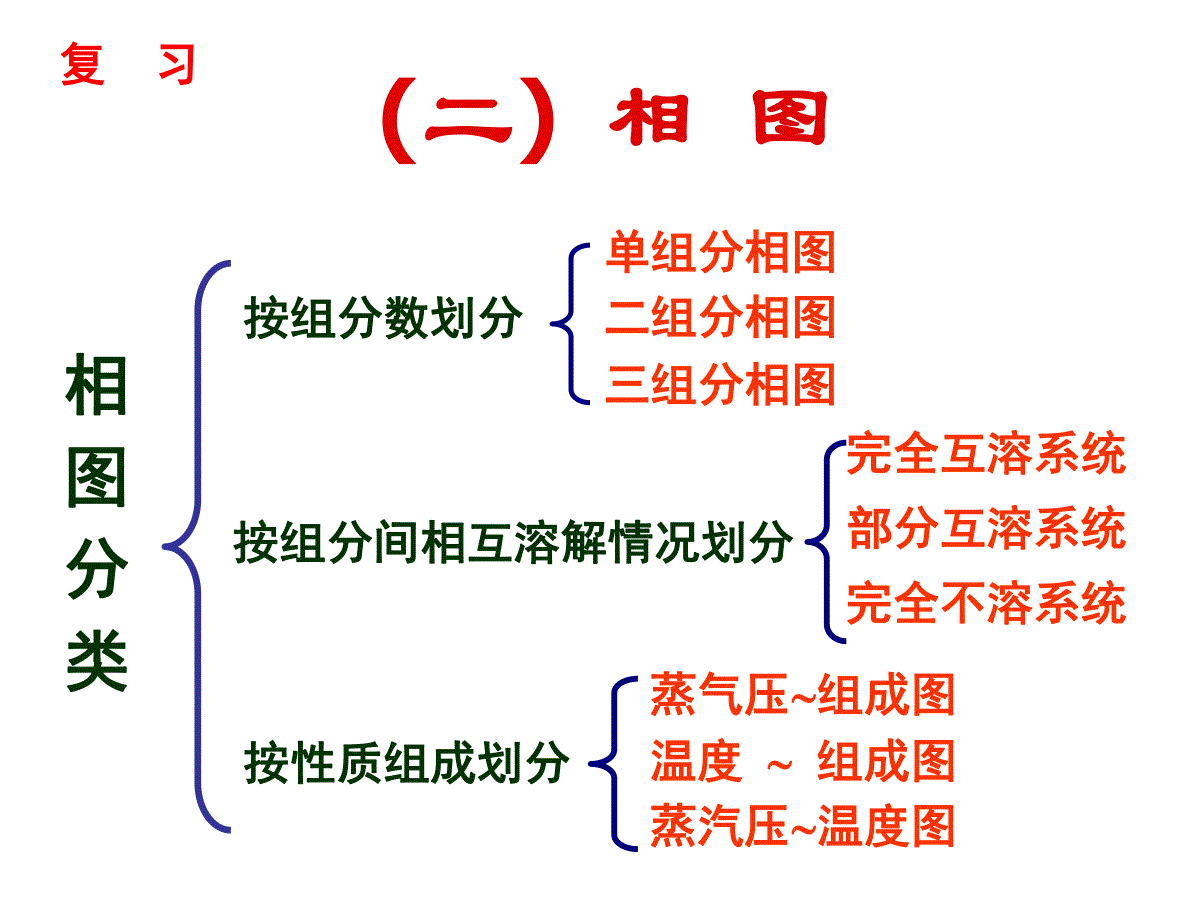
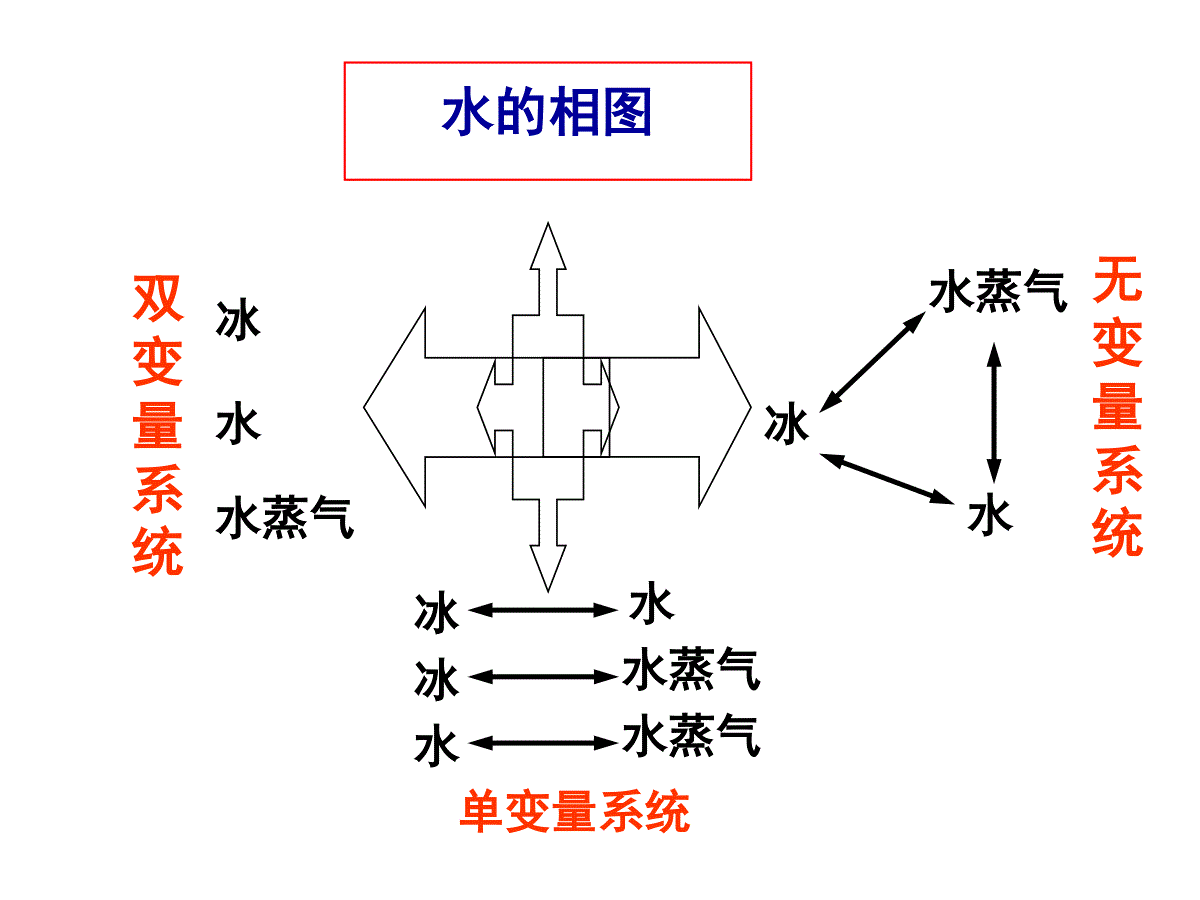
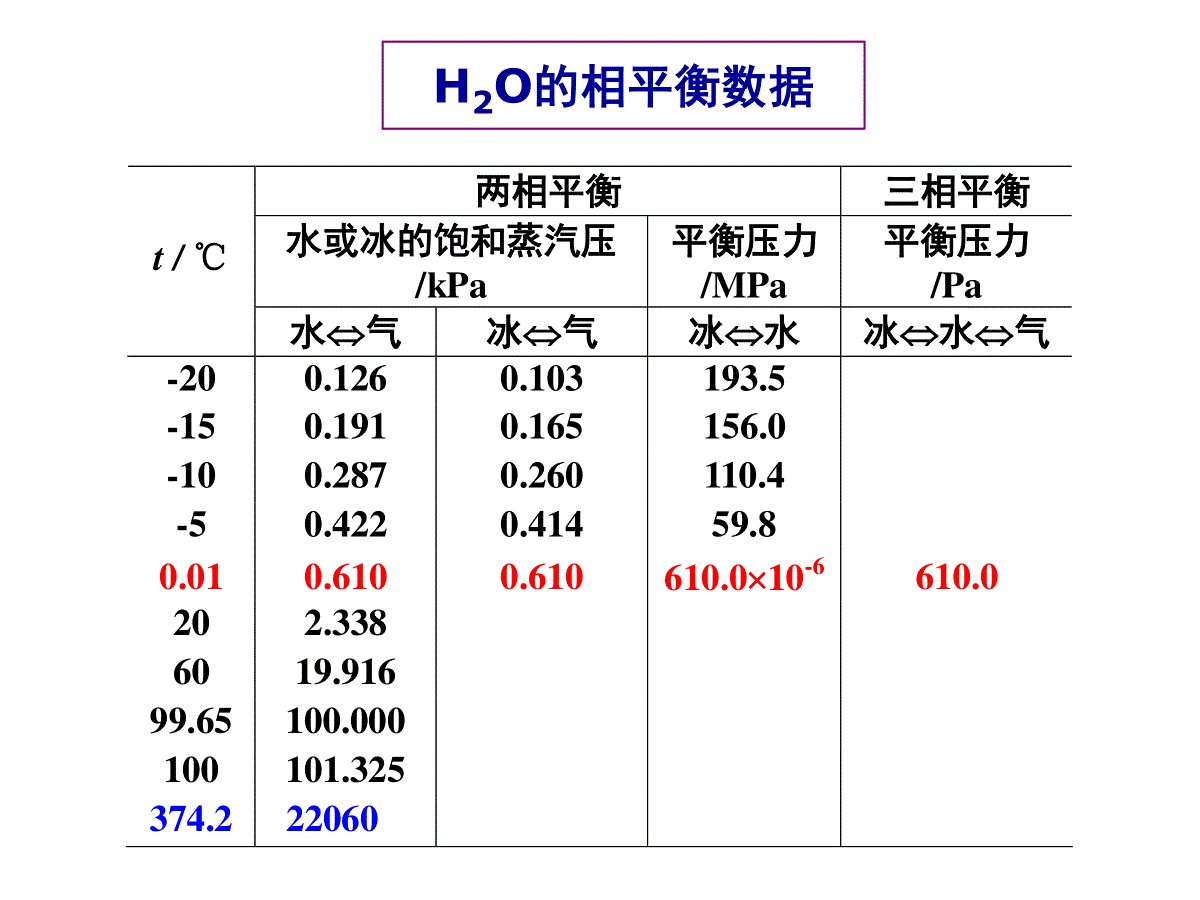
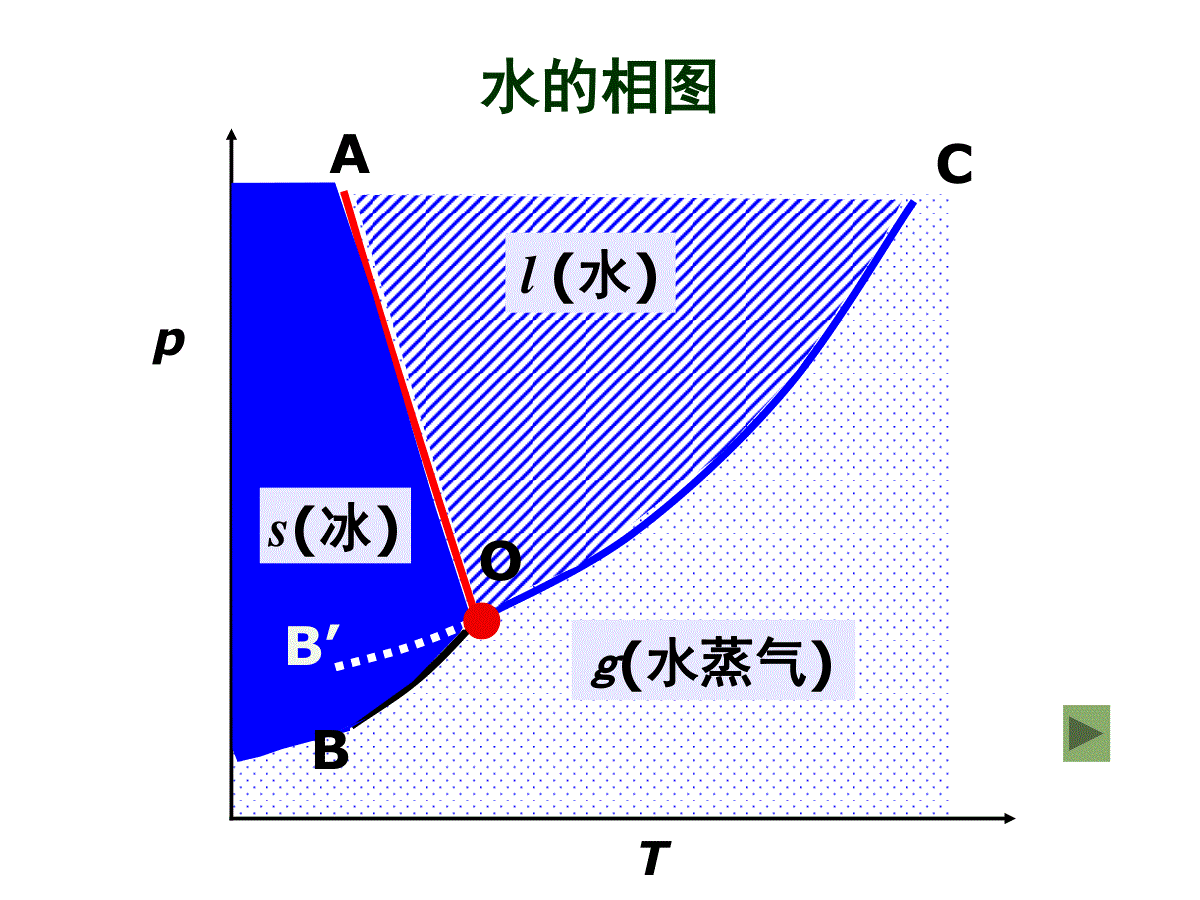
(二)相图按组分数划分单组分相图二组分相图三组分相图按性质组成划分蒸气压组成图温度组成图蒸汽压温度图按组分间相互溶解情况划分完全互溶系统部分互溶系统完全不溶系统相图分类复习(1)单组分系统相图单组分:C=1相律:F=3–PP=1:Fmax=2(双变量系统:P-T图)P＝2:F＝1(单变量系统)Pmax=3:F=0(无变量系统)水的相图水水蒸气冰双变量系统冰水蒸气水水蒸气冰水单变量系统冰水水蒸气无变量系统两相平衡三相平衡水或冰的饱和蒸汽压/kPa平衡压力/MPa平衡压力/Pat/℃水气冰气冰水冰水气-200.1260.103193.5-150.1910.165156.0-100.2870.260110.4-50.4220.41459.80.010.6100.610610.010-6610.0202.3386019.91699.65100.000100101.325374.222060H2O的相平衡数据水的相图CTpl(水)g(水蒸气)s(冰)OABB’●读图要点:①读懂点、线、面(区)的含义;②相区自由度数;③明确三相点与冰点的区别.④会描述系统状态变化情况;OC线:气-液两相平衡线,即水的饱和蒸气压曲线.C可终止于临界点；O点可延长至三相点.647KT72.210PapOB线:气-固两相平衡线,即冰的升华曲线,理论上可延长至绝对0K附近。OA线:液-固两相平衡线,即水的凝固点降低曲线,当A点延长至压力大于时,冰发生晶型转变,相图变得复杂.8210PaF=1单变量系统读图三条两相平衡线的斜率均可由Clapeyron方程或Clausius-Clapeyron方程求得。OC线:vapm2dlndHpTRTvapm0H斜率为正OA线:ubm2dlndsHpTRTfusmfus00HV，斜率为负OB线:fusmfusddHpTTVsub0H斜率为正两相平衡线的斜率OB’线:CO线的延长线,是过冷水和水蒸气的介稳平衡线.因为在相同温度下,过冷水的蒸气压大于冰的蒸气压,所以OB’线在OB线之上.过冷水处于不稳定状态,一旦有凝聚中心出现,就立即全部变成冰。O点:三相点(triplepoint),气-液-固三相共存.三相点是物质自身的特性,不能随意改变:273.16K;610.0PaP=3:F=0(无变量系统)F=0无变量系统AOC区:液态水单相区.AOB以左区域:固态水单相区.BOC以右区域:气态水单相区.P=1F=2F=2双变量系统在单相区,温度和压力独立、有限度地变化不会引起相的改变。NOTE1、水的凝固点、冰点及三相点的区别凝固点——指定压力下，水的固相与液相平衡共存的温度。OA线上任一点的横坐标值都是相应压力下水的凝固点(无数个)。冰点——在大气压力下，被空气饱和了的水的凝固点：0℃,大气压力(101.325kPa)(水的冰点随外压改变)。三相点——纯水的气、液、固三相平衡共存时的特定温度、压力决定的相点:0.01℃,610Pa(水的三相点只有一个)。水的凝固点很好区分，但水的三相点与冰点需要特别区分:水的冰点为何比三相点低0.01℃？原因有两个:纯水的三相点及“水”的冰点的区别水蒸气p=610Pa冰t=0.01℃三相点(a)在密闭容器中纯水水蒸气+空气p=101.325kPa冰t=0℃冰点(b)在敞口容器中空气饱和了的水三相点与冰点的区别101.3kPa610Pa273.15K273.16K•••(1)因外压增加，使凝固点下降；0.00748K纯水的三相点及“水”的冰点的区别压力为p=101.325kPa时，根据Clapeyron方程:t8()100715273.16(9.05510)K0.0074K333.5ffusmfusmppTVTH凝固点降低0.0074℃;水中溶入空气,形成二组分稀溶液，常压下空气的溶解度:b=0.00130molkg-1,Kf=1.855Kkgmol–1,凝固点下降：ΔT=Kf·b=0.001301.855K=0.00241K(2)因水中溶有空气，使凝固点下降。0.00241K冰点降低0.00241℃.总结果使水的三相点比冰点高0.00981℃.国际上规定:将水的三相点取为273.16℃。相点:表示某个相状态(如相态、组成、温度等)的点称为相点。物系点:相图中表示体系总状态的点称为物系点.2、相图及其应用在单相区，物系点与相点重合；在两相区中，只有物系点，它对应的两个相的组成由对应的相点表示。相图应用:由相图可以直观得出在外界条件改变时，系统状态发生什么样的变化。如：2、温度T下,系统状态从g点h点变化的情况.1、压力p下,系统状态从a点b点变化的情况.水冰气BB'ACa'bb'apbTaT相律：F=2–PggpThhpog'a点:冰aa’:P=1,F=1a’点:冰水P=2,F=0,T不变a’b’:水P=1,F=1b’点:水水气P=2,F=0,T不变b’b:水蒸气P=1,F=1读图要点①读懂点、线、区的含义;②注意OA线的倾斜方向;③三相点的p、T数值;④干冰的升华条件;⑤超临界萃取.CO2的p-T图及超临界CO2流体-60-40-20020406080100B5101520253035-56.6℃tc=31.06℃t/℃图3-2CO2相图及其体积质量(kg·m-3)与压力,温度的关系oC气液固超临界流体100200300400500600700800900100011001200p/MPapc=7.38MPaA0.518MPaCO2相图及其密度与压力、温度的关系超临界流体读图要点①读懂点、线、区的含义;②三相点的个数;③最多平衡共存的相数.Et/℃80120160lnp/105Pa10210010-210-410-6104单斜硫气态硫正交硫液态硫BC硫的相图硫的p(对数坐标)–T图(2)二组分系统相图二组分:C=2相律:F=4–PPmin=1:Fmax=3(三变量系统)P＝2:F＝2(双变量系统)P=3:F=1(单变量系统)Pmax=4:Fmin=0(无变量系统)立体图要完整表示二组分系统相平衡关系,需用三维空间坐标(立体图)表示.为了方便研究，常常保持一个变量固定,从立体图上得到平面截面图:(1)保持温度不变，得p-x图,较常用;(3)保持组成不变，得T-p图,不常用.(2)保持压力不变，得T-x图,常用;pxTT-xp-x二组分系统相图分类气-液相图液-固相图完全互溶双液系部分互溶双液系不互溶的双液系生成低共熔混合物系统生成化合物系统形成固态溶液系统两个纯液体可按任意比例互溶，每个组分都服从拉乌尔定律，这样组成了理想的完全互溶双液系，或称为理想的液体混合物，如苯和甲苯，正己烷与正庚烷等结构相似的化合物可形成这种双液系。1、完全互溶双液系理想的完全互溶双液系（即§6.3）二组分气-液系统相图理想液态混合物xBpT一定（1）二组分理想液态混合物的p-x图p=(pB*-pA*)xB+pA*特点:(1)pB*ppA*pB*BApA*xBpT一定(2)pxB线：液相线(3)pA*p，yAxApB*p，yBxB***ABABAA(-)+pyppxpBA1yy二组分理想液态混合物的p-x-y图p=(pA*-pB*)xA+pB*如果，则，即易挥发的组分在气相中的含量大于其在液相中的含量，反之亦然。**ABppAAyx在等温条件下，p-x-y图分为三个区域。在液相线之上，体系压力高于任一混合物的饱和蒸气压，气相无法存在，是液相区。在气相线之下，体系压力低于任一混合物的饱和蒸气压，液相无法存在，是气相区。在液相线和气相线之间的梭形区内，是气-液两相平衡区。亦称为沸点-组成图。外压为大气压力，当溶液的蒸气压等于外压时，溶液沸腾，这时的温度称为沸点。某组成的蒸气压越高，其沸点越低，反之亦然。T-x图在讨论蒸馏时十分有用，因为蒸馏通常在等压下进行。T-x图可以从实验数据直接绘制。也可以从已知的p-x图求得。（2）二组分理想液态混合物的T-x图从p-x图求对应的T-x图右图为已知的苯与甲苯在4个不同温度时的p-x图.在压力为处作一水平线,与各不同温度时的液相线分别交在x1，x2，x3和x4各点,代表了组成与沸点之间的关系,即组成为x1的液体在381K时沸腾,余类推。p将x1，x2，x3和x4的对应温度连成曲线就得液相线(红色线)将组成与沸点的关系标在下一张以温度和组成为坐标的图上，就得到了T-x图。理想液态混合物的T-x图和分别为甲苯和苯的沸点。显然大者，低.*pbT*BT*AT用求出相应的气相组成线(绿色线).AApyp在T-x图上,气相线在上,液相线在下,上面为气相区,下面为液相区,梭形区为气-液两相区.Note:(a)与p~x图比较，T~x图的形状、位置发生了变化。因溶液的沸点是当其蒸汽压与外压相等时，溶液所具有的温度。若外压一定，则在定温下蒸汽压高的物质在定压下其沸点低。从而，若在p~x图上有较高点，则在T~x图上有较低点。并且具有低沸点的组分在蒸气相中的浓度大于它在液相中的浓度。在T-x图上,气相线在上,液相线在下,上面为气相区，下面为液相区,梭形区为气-液两相区。Note:(b)液相线又称泡点线；气相线又称露点线。(c)液体混合物与纯液体不同：纯液体在定压下沸点是恒定的，从开始沸腾一直到液相全部转化成气相为止，温度与压力始终保持不变。而溶液的沸点在定压下不是恒定不变的，从沸腾开始到全部气化有一温度区间，称为沸腾温度区间。把p-x图和T-x图合在一起,就得到T-p-x三维图.三个坐标分别代表p，T和x。右垂直面，则压力和温度坐标分别代表纯A组分的饱和蒸气压和沸点；AB1,0xx*Ap*AT理想液态混合物的T-p-x图左垂直面上是和，连线和分别代表了纯A和纯B的蒸气压随温度的变化曲线。*Bp*BT**AApT**BBpT在共存区的上前方是高温、低压区,所以是气相区;在共存区的后下方,是低温、高压区,是液相区.理想液态混合物的T-p-x图气-液两相共存的梭形面沿和两线移动，在空间画出了一个扁圆柱状的空间区，这是气-液两相共存区。**AApT**BBpT立体图中，与最前面的平面平行的所有垂直截面是等压面，可获得T-x图；与最上面的平面平行的所有水平截面为等温面，得p-x图。（3）杠杆规则(leverrule):ngnlG(yB)OL(xB)xB,oO——物系点L——液相点G——气相点GL——结线杠杆规则表示了多组分系统任意两相平衡时，两相数量之比与两相组成、系统组成之间的关系。由(1)、(2)得:总物料衡算:n=nl+ng(1)B物质的物料衡算:nxB,o=nlxB+ngyB(2)B,oBBB,oOGLOlgx-yn=nx-x即:两相平衡时,两相的数量反比于系统点O到两个相点线段的长度:OGLOlgn=n力1力臂1=力2力臂2气相区气相液相区xAxA,0GLOxAyAAA,0A,0Algyxn=nxxOGLOlgn=nNOTE:(1)杠杆规则在任何两相平衡区都适用。(2)组成可用摩尔分数或质量分数表示，由杠杆规则相应求得两相物质的量或两相的质量；(3)杠杆规则其他表示:B,0BBBOGGLlxyn=nxyp-x(y)图1、理想的完全互溶双液系T-x(y)图T-x(y)图T-x(y)图复习在T-x图两相区,物系点O代表了系统总组成和温度.通过O点作平行于横坐标的等温线,与液相和气相线分别交于L点和G点.LG线称为结线(tieline).落在LG线上所有的物系点对应的液相和气相组成，都由L点和G点的组成表示.复习2、杠杆规则(Leverrule)气相区气相液相区xAxA,0GLOxAyA气相区气相液相区xAxA,0GLOxAyAAA,0A,0Algyxn=nxxOGLOlgn=n构成理想液态混合物的系统极少,绝大多数二组分完全互溶系统是非理想的,称为真实液态混合物.一定温度下,真实液态混合物除了在xB=1附近极小的浓度范围内,组分B的蒸汽压近似遵循R